Mathématiques : contrôle continu première technologique 20 / 01 / 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . ..... Exercice 2. 5 points. En 2019 le chiffre d'affaires d'un restaurant gastronomique était de 300 000 €. On modèlise ce chiffre pendant l'année 2019 +n par le n-ième terme de la suite (un) définie par : u0 = 300 et un+1=1,2 un -50 ( en milliers d'euros). 1. Montrer que selon ce modèle, le chiffre d'affaires sera de 310 000 € en 2020. u1 = 1,2 x u0-50 =1,2 x 300-50 =310 milliers d'euros ( 310 000 € ) 2. Calculer u2 et interpréter le résultat. u2 = 1,2 x u1-50 =1,2 x 310-50 =322 milliers d'euros ( 322 000 € ) 3. Faire une conjecture sur le sens de variations de la suite. Expliquer la démarche. un+1 - un =1,2 un -50 -un =0,2 un -50. Or un > u0 ; 0,2 un > 50 ; un+1 - un >0 ; un+1 > un . La suite est croissante. Ou bien : u0 = 300 ; u1 = 310 ; u2 = 322 ; u3 = 336,4. 4. Montrer que cette suite n'est ni arithmétique, ni géométrique. un+1 - un =0,2 un -50. un+1 - un n'est pas égale à une constaante : la suite n'est pas arithmétique. un+1 / un =0,2 -50 / un. un+1 / un n'est pas constante : la suite n'est pas géométrique. 5. Si on exécute l'algorithme ci-dessous, à la fin k = 9. Comment peut-on interpréter ce résultat ? u = 300 k=0 while u < 500 u=u*1,2u-50 k=k+1. k = 9 ( année 2008), le chiffre d'affaires dépasse 500 000 €. . .. ... . . Exercice 3 ( 5 points). Soit f la fonction définie sur R par f(x) = -2x2+6x+8. 1. Montrer que f(x) = -2(x+1)(x-4). On développe : -2 ( x2+x-4x-4) = -2(x2-3x-4) = -2x2+6x+8. 2. Résoudre l'équation f(x) = 0. x+1=0 ; x = -1 ; x-4=0 ; x = 4. 3. Faire un schéma de l'allure de la courbe représentative de f. 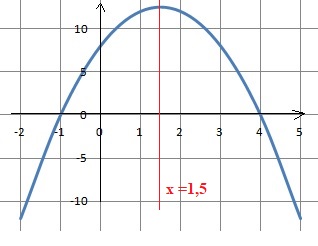4. Expliquer pourquoi le maximum est atteint pour x = 1,5. Le maximum est atteint pour x = -b / (2a) soit x = -6 / (2 *(-2)) = 6 / 4 = 1,5. l'axe de symétrie de la courbe est la droite d'équation x = 1,5. 5. Dresser le tableau de variation de f sur l'intervalle [-1 ; 4]. . .   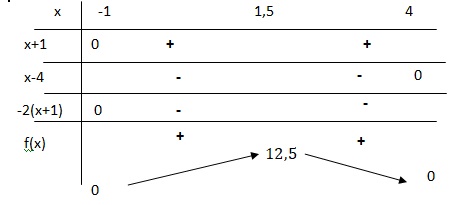Exercice 4. ( 5 points). Un fabricant d'ampoules possède deux machines A et B. La machine A fournit 65 % de la production. Certaines ampoules présentent un défaut : 8 % à la sortie de la machine A et 4 % à la sortie de la machine B présentent un défaut. On produit 15 000 ampoules par jour. 1. Combien d'ampoules proviennent de chaque machine ? Machine A : 15 000 x0,65 =9 750. Machine B : 15 000-9 750 =5 250. 2. Compléter le tableau suivant : Machine A Machine B  Total Avec défaut 780 5250 x 0,04=210 990 Sans défaut 8970 5040 14 010 Total 9750 5 250 15000 3. Calculer la fréquence en pourcentage des ampoules ayant un défaut. 990 / 15 000 x100 = 6,6 %. 4. On définit les événements : A : " l'ampoule provient de la machine A". D : " l'ampoule présente un défaut". Déterminer A n D. 780 / 15000 =0,052 (5,2 %). Ou bien 0,65 x 0,08 =0,052. .. .

menu