Mathématiques.
E3C, contrôle continu première technologique
01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice
2.
Un
comité d'entreprise souhaite organiser un wek-end à Rome. Une enquète
est faite auprès de 1200 employés afin de connaître leur choix en
matière de moyen de transport.
|
Train
|
Avion
|
Autocar
|
Total
|
Femmes
|
468
|
196
|
56
|
720
|
Hommes
|
150
|
266
|
64
|
480
|
Total
|
618
|
462
|
120
|
1200
|
On interroge au hasard un employé et on noteles événements :
F " être une femme".
T " l'employé choisit le train"
1. Calculer les probabilité P(F) et P(T).
P(F) = 720 / 1200 =0,6.
P(T) =618 / 1200 =0,515~0,52.
2. Calculer la probabilité que l'employé choisi ne prenne pas le train.
(612 +120) /1200 ~0,485 ~0,49.
Ou bien 1 -P(T)=1-0,515 = 0,485 ~0,49.
3. Que représente l'événement (F n T) et calculer sa probabilité.
L'employé est une femme qui choisit le train.
P(F n T) =468 / 1200 =0,39.
4. L'employé interrogé a choisi le train. Calculer la probabilité que celui-ci soit une femme.
PT(F)= 468 / 618 =0,757 ~0,76.
5. Calculer P F(T).
468 / 720 =0,65.
|
| .
. |
.
.
|
Exercice 3 .
Un apiculteur vend des cartons de pots de miel. Le coût en euros de production de n cartons ( n < 120) est modélisé par le nombre C(n) où C est la fonction définie sur [0 ; 120] par C(x) =0,25 x2 +500.
1. Calculer le coût de fabrication de 40 cartons.
C(40) = 0,25 x402 +500 =900.
2. On considère le bénéfice en euros réalisé après la production et la vente de n cartons. Il est modèlisé par B(x) =-0,25x2 +30x -500.
Montrer que B(x) = -0,25(x-20)(x-100).
On développe : B(x) = (-0,25x +5)(x-100)= -0,25x2+25x+5x-500 = -0,25x2 +30x -500.
3. Déterminer le tableau de signes de B(x).
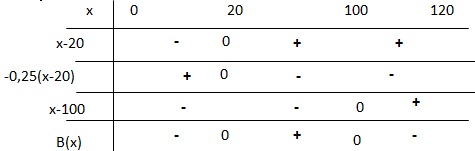
4. Combien de carton faut-il vendre pour réaliser un bénéfice ?
Entre 20 et 100 cartons. ]20 ; 100[.
5. Déterminer le nombre de cartons à produire et vendre pour un bénéfice maximal.
x = -b /(2a) = -30 / (2 x(-0,25) = 60.
ou bien 20 +(100-20) / 2 = 60.
|
Exercice 4.
Deux
amis A et B débutent dans deux entrprises différentes. Au 1er janvier
de l'année 2019, A et B ont le même salaire mensuel de 1500 €.
Le salaire de A augmente chaque année de 2,5 %. Son montant en euros est modélisé en 2019 +n par une suite (an) de premier terme 1500.
Le salaire de B augmente chaque année de 35 €. Son montant en euros est modélisé en 2019 +n par une suite (bn) de premier terme 1500 etde raison 35.
1. Calculer le salaire de A en 2020 et 2021.
100 +2,5 = 102,5 ; coefficient multiplicateur 1,025.
En 2020 : 1500 x1,025 =1537,5 €.
En 2021 : 1537,5 x1,025 =1575,94 €.
2. Justifier que an+1 = 1,025 an et en déduire la nature de la suite.
100 +2,5 = 102,5 ; coefficient multiplicateur 1,025.
an+1 / an =1,025, suite géométrique.
3. Donner le contenu de la variable n après exécution de l'algorithme suivant et interpréter le résultat.
n =0
a = 1500
while a <1650 :
n = n+1
a = 1,025*a
n
|
1
|
2
|
3
|
4
|
a
|
1537,5
|
1575,94
|
1615,34
|
1655,72
|
a < 1650
|
faux
|
faux
|
faux
|
vrai
|
n = 4 ( année 2023).
|
.
|
|