Mathématiques, QCM, fonction, suite, probabilités. enseignement de spécialité première générale.

Mathématiques, QCM, fonction, suite, probabilités.
enseignement de spécialité première générale.

. .

Sujets 1 et 2.
Exercice 1. ( 5 points ).
QCM ( aucune justification n'est demandée)
1. ABC est un triangle tel que AB = 5, AC = 6 et .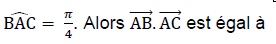
a) 15 x2^½ vrai ; b) 15 x3^½ ; c) 7,5 ; d)15.
AB *AC * cos(45) = 5 x 6 x 2^½ / 2 = 15 x2^½.

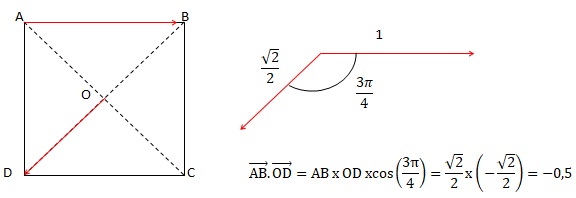
2. ABCD est un carré de centre O tel que AB = 1.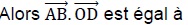
a) 1 ; b) 0 ; c) -0,5 ; d) -1.

3. On considère deux vecteurs orthogonaux tels que :

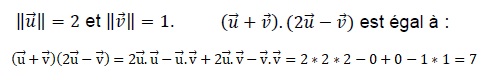
4. On se place dans un repère orthonormé du plan.
Sur la figure ci-dessous, on a tracé la courbe représentative notée 𝐶 d’une fonction 𝑓 définie sur ℝ. La droite 𝐷 est tangente à la courbe 𝐶 au point A(5;0).
On note 𝑓 ′ la dérivée de la fonction 𝑓. Alors 𝑓 ′(5) est égal à :
a) 3 ; b) -3 ; c) 1 /3 ; d) -1/3.

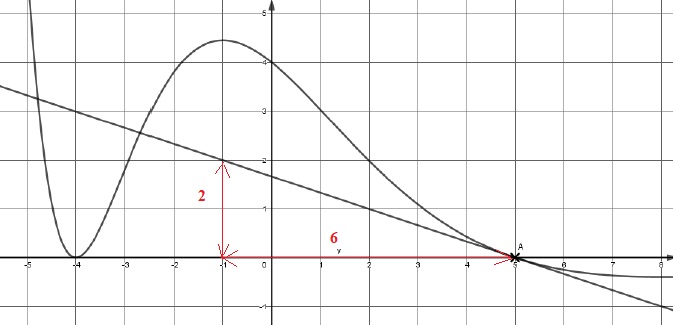
f '(5) = coefficient directeur de la tangente à la courbe en x = 5 : -2 / 6 = -1 / 3

5. Pour tout réel 𝑥 de l’intervalle ]−∞;0], on a :
a) f '(x) < 0 ; b) f '(x) > 0 ; c) f(x) > 0 vrai ; d) f(x) < 0.

Sujet 2.
1. L'équation e^-2x > 0 a pour ensemble de solution.
R, vrai. ; ]0 ; + oo[ ; ] -oo ; 0[ ; aucune solution.

2. Pour tout réel x, (e^x-1)² est égal à :
e^2x-1 ; e^2x+1 ; e^2x-2e^x+1 vrai ; exp(x)² -1.

3. Soit la fonction f définie sur R par f(x) = e^5x-1. Pour tout réel x, f '(x) est égale à :
e^5x-1 : 5 e^5x ; 5 e^5x-1 vrai ; 5x e^5x-1.

4. Dans un repère orthonormé, la droite passant par A(4 ; 7) et de vecteur normal de coordonnées (-1 ; 3) a pour équation :
. 3x+y-19 = 0 ; 3x+y+19 = 0 ; -x+3y +17 =0 ; -x+3y-17 =0 ; vrai
Une équation cartésienne est de la forme -x+3y +c = 0.
A appartient à la droite, donc :-4 +3 *7 +c =0 ; c = -17.

5. On considère l'équation du cercle x²-4x+(y+3)²=3.
Son centre a pour coordonnées : (-2 ; -3 ) ; (2 ; -3) vrai ; (-4 ; 3) ; (4 ; -3).
x²-4x+4 -4 +(y+3)²=3 ; (x-2)² +(y+3)²=7.

Exercice 2. ( 5 points) Sujet 1.

Une entreprise pharmaceutique fabrique un soin antipelliculaire. Elle peut produire entre 200 et 2 000 litres de produit par semaine. Le résultat, en dizaines de milliers d’euros, réalisé pour la production et la vente de x centaines de litres est donné par la fonction R définie par :
R(x)=(5x−30) e^-0,25x, pour tout réel x∈[2;20]
1) Calculer le résultat réalisé par la fabrication et la vente de 7 centaines de litres de produit. On l’arrondira à l’euro près.
x = 7 ; R(7) = (35-30)e^-1,75 =0,8688697 dizaines de milliers d'euros = 8688,70 €..
2) Vérifier que pour la fabrication et la vente de 400 litres de produit, l’entreprise réalise un résultat négatif (appelé déficit).
x = 4 ; R(4) = (20-30) e^-1= -3,6788 dizaines de milliers d'euros.
3) Résoudre l’inéquation R(x) ≥ 0, d’inconnue x. Interpréter dans le contexte de l’exercice.
Le terme en exponentielle est toujours positif ; R(x) > 0 équivaut à 5x-30 > 0 soit x > 6.
A partir de 600 litres fabriqués, on fait un bénéfice.
4) On note R'′ la dérivée de la fonction R.
Un logiciel de calcul formel donne : R'(x)=(−1,25x+12,5)e^-0,25x.
En déduire la quantité de produit que l’entreprise doit produire et vendre pour réaliser le résultat maximal.
R'(x) =0 soit -1,25x +12,5 = 0 ; x = 10 soit 1000 litres.

Sujet 2.
Une chaîne de salons de coiffure propose à ses clients qui viennent pour une coupe deux prestations supplémentaires cumulables :
— une coloration naturelle à base de plantes appelée « couleur-soin »,
— des mèches blondes pour donner du relief à la chevelure, appelées « effet coup de soleil ».
Il apparaît que 40% des clients demandent une « couleur-soin ». Parmi ceux qui ne veulent pas de « couleur soin », 30% des clients demandent un « effet coup de soleil ». Par ailleurs, 24% des clients demandent une « couleur soin » et un « effet coup de soleil ».
On interroge un client au hasard.
On notera C l’évènement « Le client souhaite une "couleur-soin." ».
On notera E l’évènement « Le client souhaite un "effet coup de soleil." ».
1. Donner les valeurs de P(C), P(C ∩E) et P_C (E).
P(C) = 0,40 ; P(C ∩E) =0,24 ; P_C (E) =P(C ∩E) / P(C) =0,24 / 0,4 =0,60.
2. Calculer la probabilité que le client ne souhaite ni une « couleur-soin », ni un « effet coup de soleil ».
0,6 x0,7 = 0,42.
3. Montrer que la probabilité de l’évènement E est égale à 0,42.
Formule des probabilités totales.

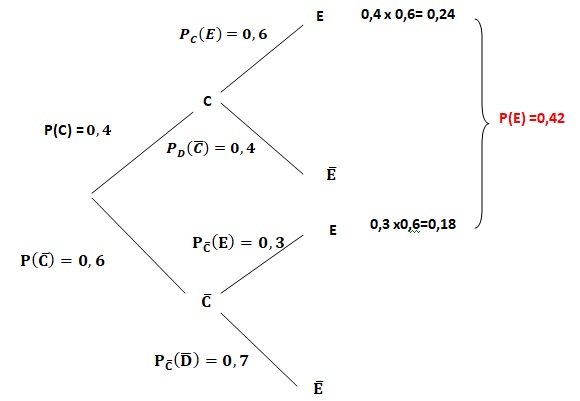
4. Les évènements C et E sont-ils indépendants ?
P(C) x P(E) =0,40 x0,42 =0,168 diffère de P(C ∩E) : les événements C et E ne sont pas indépendants.

Exercice 3. ( 5 points). Sujet 1.
Lors du lancement d’un hebdomadaire, 1 200 exemplaires ont été vendus.
Une étude de marché prévoit une progression des ventes de 2 % chaque semaine.
On modélise le nombre d’hebdomadaires vendus par une suite (u_n) où u_n représente le nombre de journaux vendus durant la n-ième semaine après le début de l’opération.
On a donc u₀= 1 200.
1) Calculer le nombre u₂. Interpréter ce résultat dans le contexte de l’exercice.
u₁= 1,02 u₀ = 1,02 x 1200 =1224.
u₂= 1,02 u₁ = 1,02 x 1224 =1248 exemplaires vendus la seconde semaine..
2) Écrire, pour tout entier naturel n, l’expression de u_n en fonction de n.

Suite géométrique de raison 1,02 et de premier terme 1200: u_n = 1200 x 1,02ⁿ.
3) Voici un programme rédigé en langage Python :

Le programme retourne la valeur 20. Interpréter ce résultat dans le contexte de l’exercice.
Au bout de 20 semaines, le total des exemplaires vendus est supérieur à 30 000.
4) Déterminer le nombre total d’hebdomadaires vendus au bout d’un an.
1 an = 52 semaines.
S = u₀ + u₁ +u₂ +...+u₅₂
S = 1200 x (1-1,02⁵³) / (1-1,02) =111 380.

Sujet 2
Partie A.
Soit (u_n) une suite géométrique de raison 2 de premier terme u₀ = 0,2.
1. Calculer u₁₈ puis u₅₀.
u₁₈=u₀ x 2¹⁸ =0,2 x2¹⁸ =52 428,8.
u₅₀=u₀ x 2⁵⁰ =0,2 x2⁵⁰ =225 179 981 368524,8.
2. Calculer u₀ +u₁ +u₂ +u₃ +u₄ +. . .+u₁₈, c’est-à-dire la somme des 19 premiers termes de la suite (u_n).
u₀ ( 1-2¹⁹) / (1-2) =104 857,4.
3. Recopier et compléter les trois parties en pointillé de l’algorithme suivant permettant de déterminer le plus petit entier n tel que la somme des n +1 premiers termes de la suite u
dépasse 100 000.

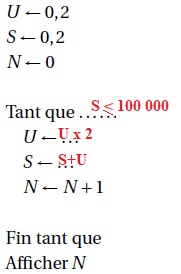
Partie B.
Claude a donné 20 centimes d’euros (soit 0,20 €) à son petit-enfant Camille pour sa naissance.
Ensuite, Claude a doublé le montant offert d’une année sur l’autre pour chaque anniversaire jusqu’aux 18 ans de Camille.
La somme totale versée par Claude à Camille permet-elle de payer un appartement à Angers d’une valeur de 100 000 € ?
Oui car : u₀ ( 1-2¹⁹) / (1-2) =104 857,4.

Exercice4. ( 5 points) Sujet 1.
Une agence de voyage propose deux formules week-end pour se rendre à Londres au départ de Nantes. Les clients choisissent leur moyen de transport : train ou avion.
De plus, s’ils le souhaitent, ils peuvent compléter leur formule par l’option « visites guidées ».
Une étude a produit les données suivantes :
 40 % des clients optent pour l’avion ;
 parmi les clients ayant choisi le train, 50 % choisissent aussi l’option « visites guidées » ;
 12 % des clients ont choisi à la fois l’avion et l’option « visites guidées ».
On interroge au hasard un client de l’agence ayant souscrit à une formule week-end à Londres.
On considère les évènements suivants :
A : « le client a choisi l’avion » ;
V : « le client a choisi l’option « visites guidées ».
1) Déterminer P_A(V).
P_A(V) =P(A n V) / P(A) = 0,12 / 0,4 =0,3.
2) Démontrer que la probabilité pour que le client interrogé ait choisi l’option « visites guidées » est égale à 0,42.
Formule des probabilités totales :

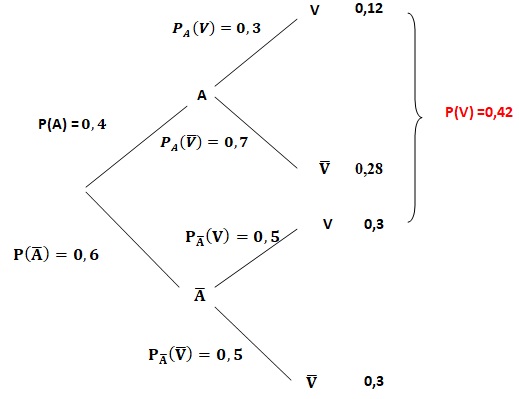
3) Calculer la probabilité pour que le client interrogé ait pris l’avion sachant qu’il n’a pas choisi l’option « visites guidées ». Arrondir le résultat au centième.
P _{non V} A =P(non V n A) / P(nonV) =0,6 x0,5 / (1-0,42) ~0,52.
4) On interroge au hasard deux clients de manière aléatoire et indépendante.
Quelle est la probabilité qu’aucun des deux ne prennent l’option « visites guidées » ?
P(non V n non V) = (1-0,42) x(1-0,42) = 0,58 x 0,58 =0,3364.

Sujet 2.
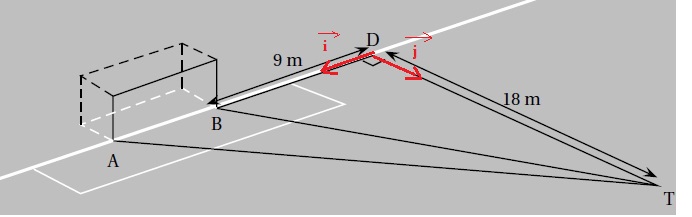
Sur le dessin ci-dessous, la largeur du but est de : AB = 7,32 mètres.
Les points A, B et D sont alignés.
On appelle T le point où se trouve un ballon. Le triangle TAD est rectangle en D.

menu