Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujets 3
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée)
1. On lance deux fois une pièce équilibrée, de manières identiques et indépendantes.
Si le joueur obtient 2 Faces, il perd 5 €, s’il obtient exactement une Face, il gagne 2 €, s’il
obtient 2 Piles il gagne 4€. On note G la variable aléatoire correspondant au gain algébrique du joueur, en euros..
E(G) =0,75 vrai ; E(G) = 1 /3 ; E(G) = 1 ; R(G) = 0,25.
Probabilité d'obtenir 2 Faces = probabilité d'obtenir 2 Piles = 0,5 x0,5 = 0,25.
Probabilité d'obtenir une Face = 0,50.
E(G) = 0,25 x(-5) +0,50 x2 +0,25 x4 =0,75.
2. A et B sont 2 événements et P(A) = 3 / 7, P(B) = 3 / 20 P( A u B) =4 / 7.
A et B sont indépendants ;
PA(B) =3 / 980 ;
P(A n B ) = 1 /140 ; vrai.
PA(B) = 1 /60.
P(A n B) =P(A) +P(B) -P(A u B) =3 / 7 +3 / 20 -4 / 7 = -1 / 7 +3 / 20 = -20 / 140 +21 / 140 = 1 / 140.
P(A n B) diffère de P(A) x P(B), A et B ne sont pas indépendants.
PA(B) =P(A n B) / P(A) = 7 / (140 x3).
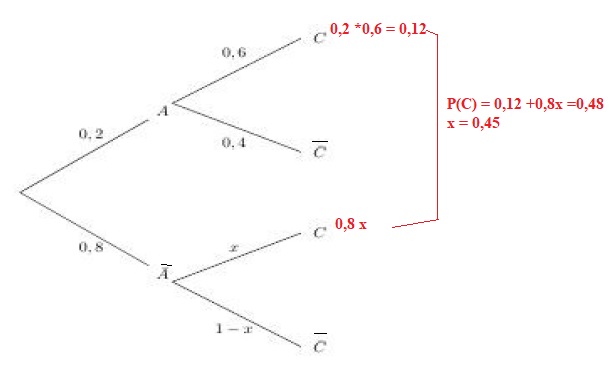
3. On donne l'arbre de probabilité ci-dessous, ainsi que P(C) = 0,48.
x = 0,6 ; x = 0,36 ; x = 0,45 vrai ; x = 0,48 / 0,12.
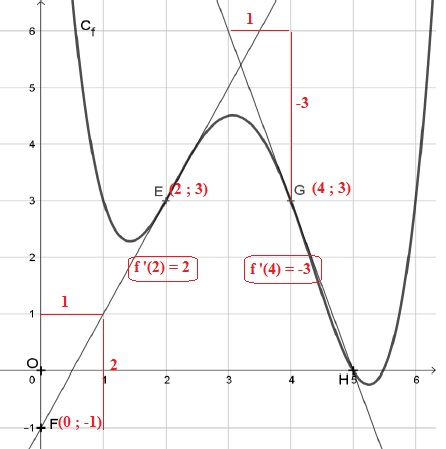
4. On a tracé la courbe représentative Cf
d’une fonction f dans un repère orthonormé, ainsi que deux de ses
tangentes, au point E d’abscisse 2 et au point G d’abscisse 4.
Les coordonnées des points E, F, G, H placés dans le repère ci-contre peuvent être lues graphiquement, ce sont des entiers.
La tangente à Cf au point E est la droite (EF).
La tangente à Cf au point G est la droite (GH).
On note f ′ la fonction dérivée de f.
f '(2) = 4 ; f '(4) = 3 ; f '(4) =3 ; f '(4) = -3 vrai.
5.On considère la fonction Python suivante :
def evolu (k) :
i= 200
n = 0
while i < k :
i= 1.2 ∗ i + 10
n = n+ 1
return n
𝑎) 𝑒𝑣𝑜𝑙𝑢(500) = 4 ; 𝑏) 𝑒𝑣𝑜𝑙𝑢(600) = 4 ; 𝑐) 𝑒𝑣𝑜𝑙𝑢(300) = 3 ; 𝑑) 𝑒𝑣𝑜𝑙𝑢(400) = 4. vrai
k
|
600
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
i
|
200
|
250
|
310
|
382
|
468,4
|
472,08
|
696,496
|
i < k
|
vrai
|
vrai
|
faux
|
vrai
|
vrai
|
faux
|
faux
|
.
Sujet 4.
1.
Dans un repère orthonormé, on considère les points A(4; 2), B(2; 6).
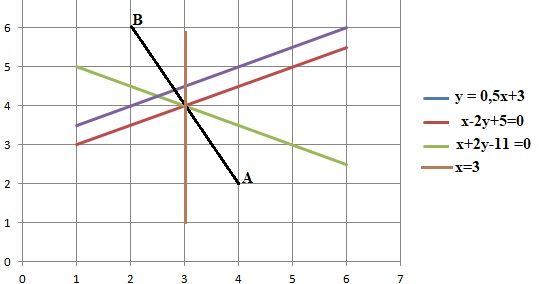
Une équation cartésienne de la médiatrice du segment [AB] est :
x = 3 ; x-2y+5 =0 vrai ; x+2y-11 = 0 ; y = 0,5x +3.
Coordonnées du milieu I de [AB] :(4+2) / 2 = 3 ; (2+6) / 2=4.
x = 3 : les coordonnées de I ne vérifient pas y = 4.
Les coordonnées de I vérifient x-2y+5 =0.
Les coordonnées de I vérifient x+2y-11 = 0.
Les coordonnées de I ne vérifient pas y = 0,5x +3.
Soit M(x ; y) de la médiatrice : AM (x-4 ; y-2) ; MA2 =(x-4)2 +(y-2)2 = x2 -8x+16+y2 -4y +4.
BM (x-2 ; y-6) ; MB2 =(x-2)2 +(y-6)2 = x2 -4x+4+y2 -12y +36.
MA = MB donne : x2 -8x+16+y2 -4y +4 = x2 -4x+4+y2 -12y +36.
-8x+16 -4y +4 = -4x+4 -12y +36.
-4x+8y-20 = 0 ; -x+2y-5=0 ou x-2y+5 =0
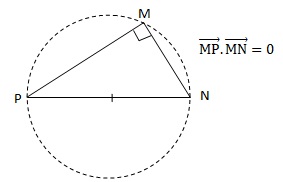
2. On donne deux points P et N tels PN = 6.
L’ensemble des points M tels que 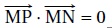 est : est :
a. la droite (PN).
b. le cercle de diamètre [PN]. vrai.
c. un cercle de rayon 6
d. le milieu du segment [PN].
3. Soit g la fonction définie sur R par g (x)= x3 −4x +5.
Une équation de la tangente à la courbe représentative de g dans un repère orthonormé au point d’abscisse −1 est :
y= 8x+7 ; y = -7x+1 ; y = -x+7 vrai ; x = -0,5.
g' =3x2-4 ; g'(-1) =-1 ( coefficient directeur de la tangente en x = -1).
Equation de la tangente : y = -x+b.
La tangente passe au point (-1 ; g(-1) =8 ) ; 8 =1+b ; b = 7.
4. l'axe de symétrie de la parabole d'équation y = x2+x+3 est :
y = x ; y = -0,5x+1 ; y = -0,5 ; x = -0,5 vrai.
x = -b /(2a) = -1 / (2*1)=-0,5.
5. l'inéquation -3ex+2 >-3e4 d’inconnue x, a pour ensemble de solutions :
]-2 ; +oo[ ; ]2 ; +oo[ ; ]-oo ; 2 [ vrai ; ]-oo ;-2[.
ex+2 < e4 ; x+2 < 4 ; x < 2.
|
|
Exercice 2. ( 5
points) Sujet 3.
Un artisan commence la pose d’un carrelage dans une grande pièce. Le carrelage choisi a une forme hexagonale.
L’artisan pose un premier carreau au centre de la pièce puis procède en étapes successives de la façon suivante :
à l’étape 1, il entoure le carreau central, à l’aide de 6 carreaux et obtient une première forme.
à l’étape 2 et aux étapes suivantes, il continue ainsi la pose en entourant de carreaux la forme précédemment construite.
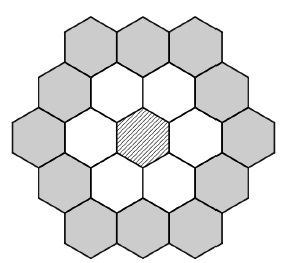
On note un le nombre de carreaux ajoutés par l’artisan pour faire la n-ième étape (n ≥ 1).
Ainsi u1 = 6 et u2 = 12.
1. Quelle est la valeur de u3 ?
u3 = 18.
2. On admet que la suite (un ) est arithmétique de raison 6. Exprimer un en fonction de n.
un = 6n.
3. Combien
l’artisan a-t-il ajouté de carreaux pour faire l’étape 5 ? Combien
a-t-il alors posé de carreaux au total lorsqu’il termine l’étape 5 (en
comptant le carreau central
initial) ?
u5 =30 ;1 + u1 +u2 +u3 +u4 +u5 =1 +6+12+18+24+30=91.
4. On pose Sn = u1 +u2 +....+un . Montrer que Sn = 6(1 + 2 + 3 + ⋯ + n) puis que Sn = 3n2 + 3n.
Sn =6 +12 +...+6n = 6(1 +2 +...+n).
Somme des terme des n premiers termes d'une suite arithmétique de raison 1 et de premier terme 1 : n(n+1) / 2.
Sn =6n(n+1) / 2 = 3n2 + 3n.
5. Si on compte le
premier carreau central, le nombre total de carreaux posés par
l’artisan depuis le début, lorsqu’il termine la n-ième étape, est
donc 3n2 + 3n + 1.
À la fin de sa semaine, l’artisan termine la pose du carrelage en collant son 2977 e carreau. Combien a-t-il fait d’étapes ?
2977 -1 = 2976 = 3n2 + 3n ; 3n2 + 3n-2976 = 0.
Discriminant : 9 +4*3*2976 =35721 ; n = (-3 +189) / 6 =31
Sujet 4.
Partie A :
(un) est une suite géométrique de premier terme u0 = 25000 et de raison 0,94.
(vn) est une suite définie par : vn = 50(104+25n) pour tout entier naturel n.
1. Déterminer une forme explicite de la suite (un).
un = u0 x0,94n = 25 000 x0,94n.
2. Calculer la somme des sept premiers termes de la suite (un).
S = u0(1-qn+1) / (1-q) =25 000 x(1-0,947) / (1-0,94)=146 4679,7.
3. Comparer les termes u0 et v0 puis u20 et v20.
v0 = 50 x104 =5200 ; v0 < u0.
u20 =25 000 x0,9420 = 7252,65 ; v20 =50x(104 +25 x 20) =30200 ; v20 > u20.
4. Déterminer le plus petit entier naturel n tel que un < vn.
u18 =25 000 x0,9418 ~ 8208 ; v18 =50x(104 +25 x 18) =27700 ;
u10 =25 000 x0,9410 ~ 13465 ; v10 =50x(104 +25 x 10) =17700 ;
u8 =25 000 x0,948 ~ 15239 ; v8 =50x(104 +25 x 8) =15200 ;
u9 =25 000 x0,949 ~ 14325 ; v9 =50x(104 +25 x 9) =16450. Réponse n = 9.
Partie B :
Un concessionnaire de voitures propose des voitures équipées d’un moteur diesel ou d’un moteur essence.
Durant
sa première année d’existence en 1995, il a vendu 25 000 véhicules avec
un moteur diesel et 5 200 véhicules avec un moteur essence.
Ses ventes de voitures avec un moteur diesel ont diminué de 6% chaque
année, alors que ses ventes de voitures avec un moteur essence ont
augmenté de 1 250 unités tous les ans.
En quelle année les ventes de voitures avec un moteur essence ont elles dépassé les ventes de voitures avec un moteur diesel ?
Diesel : suite géométrique de raison 0,94 et de premier terme 25 000 ; un = 25 000 x0,94n.
Essence : suite arithmétique de raison 1250 et de premier terme 5200 ; vn = 5200 +1250 n.
D'après la partie A, n = 9 ; 1995 +9 = 2004.
|
Exercice 3. ( 5
points). Sujet 3. Un propriétaire souhaite construire un enclos rectangulaire sur son terrain.
Celui-ci est représenté ci-dessous dans un
repère orthonormé, d’unité le mètre. Il est délimité par l’axe des
abscisses, l’axe des ordonnées, la droite d’équation x=5 et la courbe C f représentative de la fonction f définie sur [0 ; 5] par f(x)=4e-0,5x.
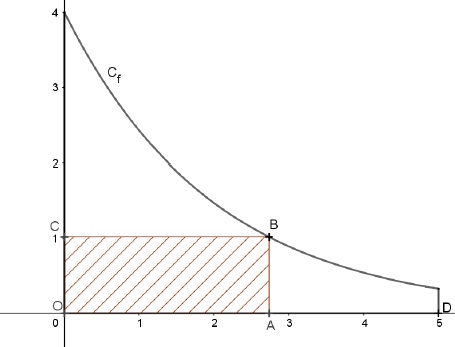
L’enclos
est représenté par le rectangle OABC où O est l’origine du repère
et B un point de C f, A et C étant respectivement sur l’axe des
abscisses et l’axe des ordonnées. On note x l’abscisse du point A et
D le point de coordonnées (5 ; 0). Le but de l’exercice est de
déterminer la position du point A sur le segment [OD] permettant
d’obtenir un enclos de superficie maximale.
1. Justifier que la superficie de l’enclos, en m2, est donnée en fonction de x par g(x)=4x e-0,5x pour x dans l’intervalle [0 ;5].
Largeur du rectangle : f(x) ; longueur : x ; aire de l'enclos : x f(x) = 4x e-0,5x .
2. La fonction g est dérivable sur [0 ;5]. Montrer que, pour tout réel x de l’intervalle [0 ; 5], on a g'(x)=(4−2x)e-0,5x.
On pose u = 4x et v = e-0,5x ; u' = 4 ; v' = -0,5e-0,5x ; u'v+v'u = 4e-0,5x -2xe-0,5x =(4−2x)e-0,5x.
3. En déduire le tableau de variations de la fonction g sur [0 ; 5].
Le terme en exponentielle est positif ; le signe de g'(x) est celui de 4-2x.
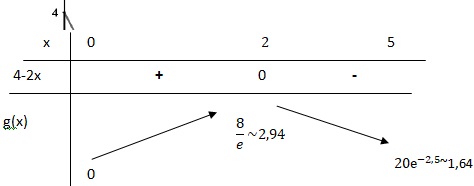
4. Où doit-on placer le point A sur [OD] pour obtenir une superficie
d’enclos maximale ? Donner la superficie maximale possible en
arrondissant le résultat au dm2.
OA = 2 m ; surface maxi : 2,94 m2 = 294 dm2.
Sujet 4.
On
dispose d’un paquet de cartes contenant un nombre identique de cartes
de la catégorie «Sciences » et de la catégorie «Économie ».Une question
liée à un de ces deux thèmes figure sur chaque carte. Les cartes sont
mélangées et on en tire une au hasard dans le paquet. Ensuite, on
essaye de répondre à la question posée.
Un groupe de copains participe à ce jeu. Connaissant leurs points forts et leurs faiblesses, on estime qu’il a :
• 3 chances sur 4 de donner la bonne réponse lorsqu’il est interrogé en sciences ;
• 1 chance sur 8 de donner la bonne réponse lorsqu’il est interrogé en économie.
On note S l’évènement « La question est dans la catégorie Sciences » et
B l’évènement « La réponse donnée par le groupe est bonne ».
Partie A :
1. Calculer P(B n S).
P(B n S) = 0,5 x0,75 = 0,375.
2. Déterminer la probabilité que le groupe de copains réponde correctement à la question posée.
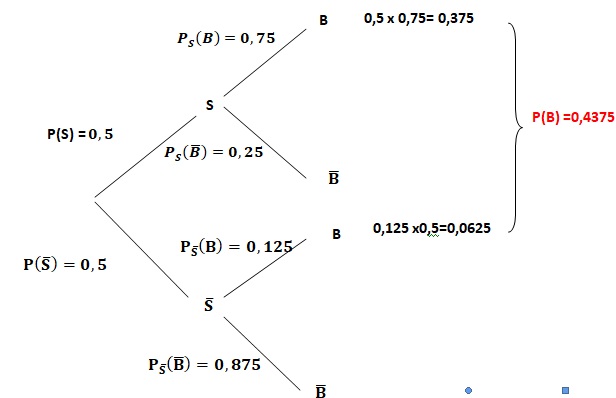
3. Les évènements S et B sont-ils indépendants ?
P(S) = 0,5 ; P(B) = 0,4375 ; P(S) x P(B) = 0,21875 différe de P(B n S).
Les événements S et B ne sont pas indépendants.
Partie B :
Pour participer à ce jeu, on doit payer 5 € de droit d’inscription. On recevra :
• 10 € si on est interrogé en sciences et que la réponse est correcte;
• 30 € si on est interrogé en économie et que la réponse est correcte;
• rien si la réponse donnée est fausse.
Soit X la variable aléatoire qui, à chaque partie jouée, associe son
gain. On appelle gain la différence en euros entre ce qui est reçu et
les 5€ de droit d’inscription.
1. Déterminer la loi de probabilité de X.
P(X =5)=0,375 ; P(X = 25) =0,0625 ; P(X = -5) =1-0,4375 =0,5625.
Gain moyen : E(X) =5 x0,375 +25 x0,0625 -5 x0,5625 =0,625.
2. Que retourne la fonction Jeu écrite ci-dessous en langage Python avec les listes :
L =[-5; 5; 25] et G = [0,5625; 0,375; 0,0625] ?
def Jeu ( L, G) :
n = len(L)
E=0
for i in range(n)
E = E+L[i]*G[i]
returne(E).
Ce programme calcul le gain moyen.
|
Exercice4. ( 5 points) Sujet 3. Le logo d’une entreprise est constitué d’un carré, d’un cercle et d’un triangle.
Il a été représenté ci-dessous dans un repère orthonormé .
On donne les coordonnées des sommets du carré :
A(−3 ; 3) ,B(3 ; 3) ,C(3 ; −3) ,D(−3 ; −3).
On considère le point E(−2 ;3+√5).
On admettra que E est situé sur le cercle de diamètre [AB].
On note I le milieu de [AB].
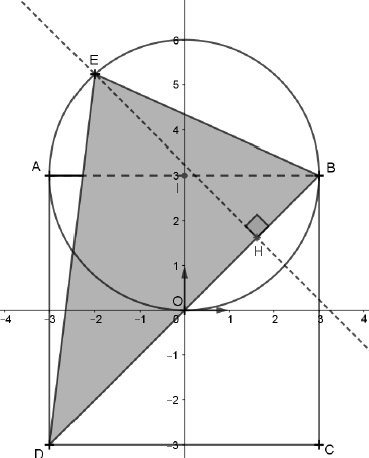
1. Donner une équation cartésienne de la droite (BD) et une équation du cercle de diamètre [AB].
La droite (BD) passe par l'origine: son équation est de la forme y = ax.
B(3 ; 3) appartient à la droite : 3 = 3a ; a = 1 ; y = x.
Centre du cercle (0 ; 3) de rayon R=3.
Equation du cercle : x2+(y-3)2 = 9.
2. Montrer que la hauteur du triangle BDE issue de E admet pour équation cartésienne x+y−(1+√5)=0.
Coefficient directeur de la droite (EH), perpendiculaire à la droite (BD) : -1.
Equation de cette droite : y = x+b.
E appartient à cette droite : 3+√5 = -1 *(-2) +b ; b = 1+√5. ; y = -x +1+√5.
3. Déterminer les coordonnées du projeté orthogonal H du point E sur la droite (BD).
H appartient à BD : xH = yH.
2xH −(1+√5)=0 ; xH = yH =(1+√5) / 2.
4. Calculer l’aire du triangle BDE (en unités d’aire).
BD * EH / 2.
BD = diagonale du carré de côté 6 cm ; BD = 6 √2.
EH : [(0,5+0,5√5+2)2 +(0,5+0,5√5-3-√5)2]½ =[ (2,5+0,5√5)2 +(-2,5-0,5√5)2]½=[ 2(2,5+0,5√5)2 ]½.
[ 2(6,25 +1,25+2,5√5) ]½ =[ 15 +5√5) ]½ .
Aire : 3 √2 [ 15 +5√5) ]½ .
5.  . .
|
Sujet 4.
On souhaite fabriquer des boîtes de rangement sans couvercle.
Les boîtes auront la forme d’un parallélépipède rectangle de hauteur 16 cm et de base un rectangle ayant pour dimensions x et y exprimées en cm.
Chaque boîte a un volume de 10 000 cm3.
1. Calculer y lorsque x = 20 cm.
10 000 = 16 x y = 16*20y ; y = 10 000 / 320 =31,25 cm.
2. Pour toute valeur de x > 0, on note f (x) l’aire du parallélépipède rectangle.
Démontrer que : pour tout x > 0, f (x) =20000 / x +32x +625
fond : xy ; aire latérale : 2*16(x+y) ; aire totale : f(x) =xy+32x+32y.
De plus xy = 10 000 /16 = 625 ; y = 625 / x.
f(x) = 625 +32x +32*625 /x = 625 +32x+20 000 / x.
3. Quelles dimensions doit-on donner à ces boîtes pour que leur surface ait une aire minimale ?
f '(x) = -20 000 /x2+32 ; la dérivée s'annule pour x2 = 20 000 /32 ; x =25.
f '(x) est négative pour x < 25 et positive pour x > 25.
f(x) présente un minimum pour x = 25 ; y = 625 / 25 =25.
Le fond est un carré de côté 25 cm.
|
|



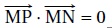 est :
est :





 .
.