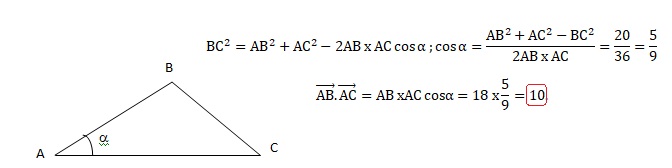Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujets 5
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée)
1. Question 1
Soit f la fonction définie sur R par f (x) = sin(x)−x. Parmi les propositions suivantes, laquelle est vraie ?
f est paire ; f est impaire vrai ; pour tout réel x, f(x+2p) = f(x) ; pour tout réel x, f(x+p) = -f(x).
f(-x) = sin(-x) -(-x) = - sin(x) +x = - [ sin(x) - x] = -f(x).
2. Dans l’intervalle ]−π ; π], l’équation 2cos(x)−3½ =0 a pour solutions :
±p/6 vrai; ±p/4 ; ±p/3 ; ±2p/3.
cos(x) = 3½ / 2 = cos (p/6) ; x = ±p/6.
3. Soit ABCD un parallélogramme tel que :

Réponse d.
4. Le plan est muni d’un repère orthonormé
On considère la droite (d1) d’équation 3x −4y +1 = 0. La droite (d2) perpendiculaire à (d1) et passant par le point A(1; 1) a pour équation :
a. 4x +3y = 0 ; b. 4x +3y −7 = 0 vrai ; c. x + y −2 = 0 ; d. −4x +3y +1 = 0.
(d1) : y = 0,75 x +0,25 ; coefficient directeur de (d2) : -4/3.
Equation de (d2) : y = -4 / 3 x +b.
A appartient à (d2) : 1 = -4 /3 +b ; b = 7 /3.
y = -4 /3x +7/3 ou 3y =-4x +7 ou 3y +4x-7 =0.
5. Le plan est muni d’un repère orthonormé d’équations respectives 2x − y +5 = 0 et −4x +2y +7 = 0 sont :
a. confondues ; b. sécantes ; c. parallèles vrai ; d. perpendiculaires.
y = 2x+5 ; coefficient directeur 2 ; y = 2x-3,5 ; coefficient directeur 2.
.
Sujet 6.
1.
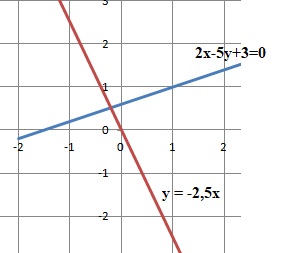
Un vecteur normal à la droite d’équation cartésienne 2x−5y+3 = 0 a pour coordonnées :
(-5 ; 2) ; (2 ; 5) ; (5 ; 2) ; (-2 ; 5).
y =0,4 x +0,6 coefficient directeur : 0,4.
Coefficient directeur de la droite perpendiculaire -1 /0,4 = -5 /2 = -2,5.
Coordonnées de ce vecteur ( 1 ; -2,5) ou ( 2 ; -5).
2. Le centre A du cercle d’équation x2 + y2 +6x −8y = 0 est :
A(3 ; 4) ; A(-3 ; 4) vrai ; A(-4 ; 3) ; A(4 ; 3).
x2 +6x +9-9 + y2−8y +16-16 = 0 ;
(x+3)2-9 +(y-4)2-16=0 ; (x+3)2 +(y-4)2=25.
3. On considère un triangle ABC tel que AB = 3, BC = 5 et AC = 6, on a alors :
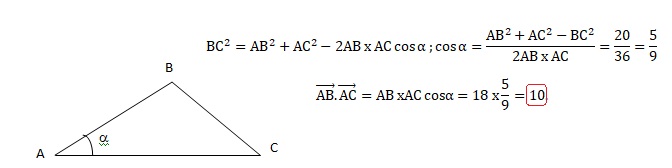
Réponse b.
4. Le nombre réel -3p /4 est associé au même point du cercle trigonométrique que le réel :
-3p /4 ± 2p soit -3p /4 ± 8p / 4 soit -11 p/4 ou 5p/4.
-3p /4 ± 4p soit -3p /4 ± 16p / 4 soit -19 p/4 ou 13p/4. Réponse c.
5. La fonction g définie sur R par g (x)= (4x −7)3 a pour fonction dérivée :
On pose u = 4x-7 ; u' = 4 ; g'(x) =3u2u' =3(4x-7)2*4=12(4x-7)2. Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 5.
Dans tout l’exercice, les résultats seront arrondis, si nécessaire, au dixmillième.
On étudie un test de dépistage pour une certaine maladie dans une population donnée. On sait que 1% de la population est atteint de la maladie. Des études ont montré que si une personne est malade, alors le test se révèle positif dans 97% des cas et si une personne n’est pas malade, le test est négatif dans 98% des cas.
Pour une personne à qui on fait passer le test de dépistage on associe les événements :
• M : la personne est malade,
• T : le test est positif.
1. Recopier et compléter sur la copie l’arbre de probabilité suivant en utilisant les données de l’exercice.
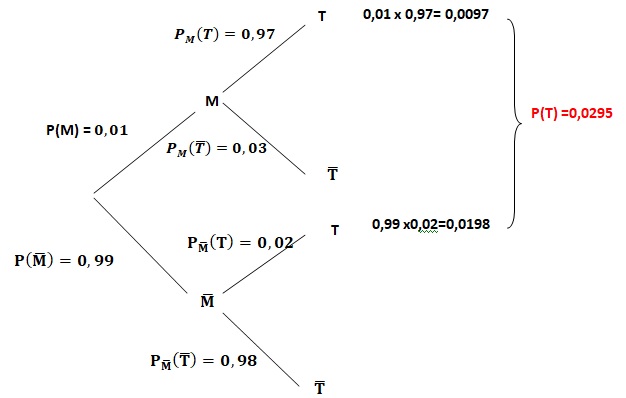
2. Justifier que P(non M n T) =0,0198
3. Montrer que P(T ) = 0,0295.
4. Calculer PT (M).
PT(M) = P(M n T) / P(T) =0,0097 / 0,0295 =0,3288.
5. Une personne dont le test se révèle positif est-elle nécessairement atteinte par cette maladie ?
Non, parmi les personnes non malades, on trouve 1,98 % de tests positifs.
Sujet 6.
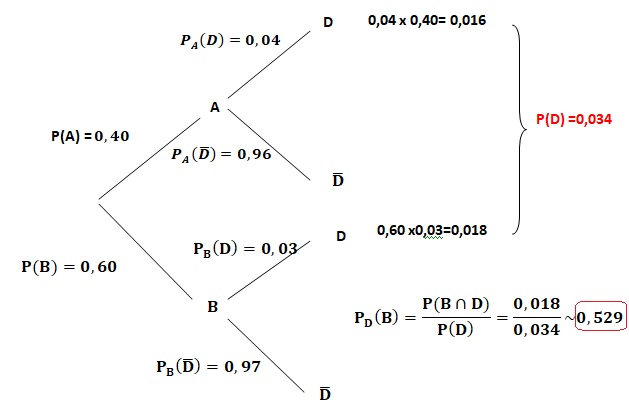
Un modèle de téléphone portable d’une grande entreprise est produit par deux sous- traitants A et B.
Chez le sous-traitant A, qui assure 40% de la production totale, 4% des téléphones sont défectueux.
Le sous-traitant B assure le reste de la production.
On constate que la probabilité qu’un téléphone pris au hasard dans les stocks de l’entreprise soit défectueux est de 0,034.
1. Quel pourcentage de la production totale le sous-traitant B assure-t-il ?
2. Quelle est la probabilité qu’un téléphone provienne du sous-traitant B sachant qu’il est
défectueux? On arrondira le résultat à 10−3 près.
|
Exercice 3. ( 5
points). Sujet 5.
On s’intéresse à la consommation d’essence d’un véhicule en fonction de sa vitesse.
Lecture graphique.
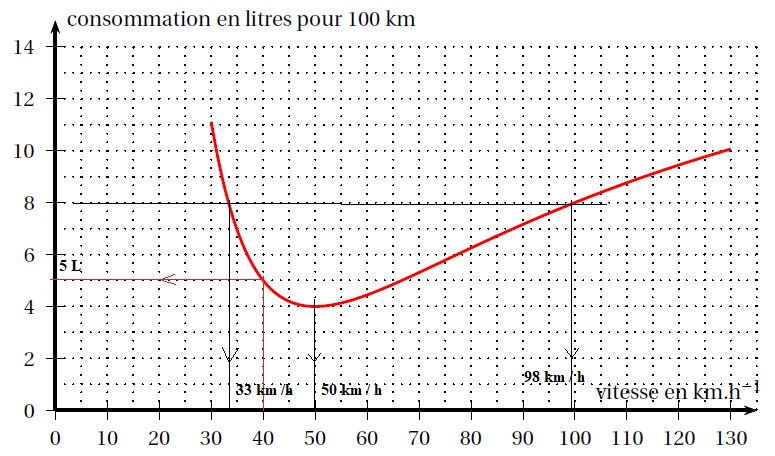
Le graphique ci-dessous représente la consommation d’essence en litres pour 100 km en fonction de la vitesse en km.h−1 du véhicule.
Avec la précision permise par le graphique, répondre aux questions suivantes :
1. Quelle est la consommation du véhicule lorsque celui-ci roule à 40 km.h−1 ?
2. Pour quelle(s) vitesse(s) le véhicule consomme-t-il 8 litres pour 100 km?
3. Pour quelle vitesse la consommation du véhicule semble-t-elle minimale ?
Modélisation
Si on note x la vitesse du véhicule en km.h−1, avec 30 < x <130, la consommation d’essence en litres pour 100 kmest modélisée par la fonction f d’expression :
f (x) = (20x2−1600x +40000) / x2 .
On désigne par f ′ la fonction dérivée de la fonction f sur l’intervalle [30; 130].
4. Montrer que pour tout x ∈ [30 ; 130], f ′(x) = 800(2x −100) / x3.
On pose u = 20x2−1600x +40000 et v = x2 ; u' =40x -1600 ; v' =2x.
(u'v-v'u) / v2 =[(40x-1600) x2-2x(20x2−1600x +40000)] /x4=[(40x-1600) x-2(20x2−1600x +40000)] /x3=(1600x -80 000) / x3 =800(2x −100) / x3.
5. Démontrer la conjoncture de la question 3.
La dérivée s'annule pour x = 50. Elle est négative pour x < 50 et positive pour x > 50.
f est décroissante pour x < 50 et croissante pour x > 50.
Sujet 6.
Soit la suite (un) de premier terme u0 = 400 vérifiant la relation, pour tout entier naturel n, un+1 = 0,9un +60.
Soit la suite géométrique (vn) de premier terme v0 = −200 et de raison 0,9.
1. Calculer u2 et v2.
u1=0,9 x400 +60 =420 ; u2=0,9 x420 +60 =438 ;
v1 = -200 x0,9 =-180 ; v2 = -180 x0,9 =-162 .
2. Calculer la somme des 20 premiers termes de la suite (vn).
v0(1-qn+1) / (1-q)= -200(1-0,920) /0,1 = -1756,84.
3. La suite (un) est-elle arithmétique? La suite (un) est-elle géométrique ?
Dans l'hypothèse d'une suite arithmétique : un+1 = un +constante.
Dans l'hypothèse d'une suite géométrique : un+1 = un fois une constante.
La suite (un) n'est ni arithmértique, ni géométrique.
4. Recopier et compléter
la fonction Suite suivante écrite en Python qui permet de calculer la
somme S des 20 premiers termes de la suite (un).
def Suite ( ) :
U = 400
S = 0
for i in range (20)
S = S+U
U = 0,9 U +60
return (S)
5. On admet que un = vn +600. En déduire u20.
v20 = -200 x0,920= -0,3594
u20 = -0,3594 +600 = 599,64.
|
Exercice4. ( 5 points) Sujet 5. On considère la suite (un) définie pour tout entier naturel n, par un =(n +2) / (n +1).
1. Calculer u0, u1,u2 puis u99.
u0 =2 ; u1 =1,5 ; u2 = 4 / 3 ; u99 = 1,01.
2. a. Exprimer, pour tout entier naturel n, un −1 en fonction de n.
un-1 =(n-1 +2) / (n-1 +1) =(n+1) / n.
b. Montrer que, pour tout entier naturel n, on a :
un+1 −un = −1 / [(n +1)(n +2)].
un+1 −un = (n+3) / (n+2) -(n +2) / (n +1) = [(n+3)(n+1)-(n+2)2] / (n+1)(n+2)= -1 / / [(n +1)(n +2)]..
c. En déduire le sens de variation de la suite (un).
Le dénominateur est positif et le dénominateur est négatif : un+1 −un < 0 ; un+1 < un.
La suite est décroissante.
3. Soit a un nombre réel dans l’intervalle ]1 ; 2].
Recopier et compléter sur la copie le programme Python suivant pour
qu’il permette de déterminer le plus petit entier naturel n tel que un < a, où a est un nombre de l’intervalle
]1; 2].
Def sruil (a)
n=0
while (n+2) / (n+1) > a :
n = n+1
return
|
Sujet 6.
On considère un cône de révolution ayant une génératrice de longueur 20 cm et d’une hauteur h en cm.
On rappelle que le volume V en cm3 d’un cône de révolution de base un disque d’aire A en cm2
et de hauteur h en cm est : V =1 /3 Ah
Dans cet exercice, on cherche la valeur de la hauteur h qui rend le volume du cône maximum.
1. Exprimer le rayon de la base en fonction de h.
202 = h2 +R2 ; R =(400-h2)½.
2. Démontrer que le volume du cône, en fonction de sa hauteur h, est :
V (h) =p /3(400h-h3)
A = p R2 =p(400-h2) ; V = 1 /3 Ah =p /3(400h-h3).
3. Quelle hauteur h choisir pour que le volume du cône soit maximum ?
Dériver V par rapport à h ; V ' = p /3(400-3h2).
V' = 0 pour h2 = 400 / 3 soit h ~11,547 cm
Si h < 11,547, V ' >0 et V fonction croissante.
Si h > 11,547, V ' < 0 et V fonction décroissante.
|
|