Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujets 7
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée)
1. Question 1
On considère les points E(3 ; −4) et F(7; 2). La droite (EF) passe par le point :
a. A(O; 8) ; b. B(5,5; 0) ; c. C(13; 11) vrai ; d. D(−25 ; 45).
Equation de la droite (EF) : y = ax +b.
E appartient à cette droite : -4 = 3a+b. (1)
F appartient à cette droite : 2 = 7a+b.(2).
(2)-(1) donne : 6=4a ; a = 6 /4 =1,5.
Par suit b = -4-3x1,5=-8,5
y = 1,5 x -8,5.
Les coordonnées du point C vérifient cette équation.
2. On considère la droite D qui a pour équation réduite y = −2x +4.
Parmi les vecteurs suivants, déterminer celui qui est un vecteur normal de la droite D :
Equation cartésienne de la droite : 2x+y-4=0
Coordonnées d'un vecteur normal de la droite D : (2 ; 1). Réponse a.
3. Soit ABCD un carré de côté 6 et I le milieu de [BC]. Alors le produit scalaire suivant vaut :
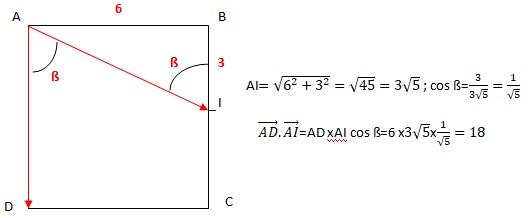
Réponse b.
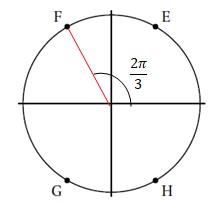
4. Sur le cercle trigonométrique ci-dessous, le nombre 14 p /3 a pour image le point :
14 p / 3 = 12 p/3 + 2p /3 = 2 x 2 p +2p/3.
5. Soit le réel x appartenant à l’intervalle [ ½p ; p] tel que sin x = 0,8. Alors cos x vaut :
cos2x + sin2x = 1 ; cos x = (1-0,82)½ = ±0,6.
x appartient à [ ½p ; p], donc cos x = -0,6. Réponse b.
.
Sujet 8.
1.  réponse a. réponse a.
2. Soit la suite définie par : u0 = 2 et un+1 = 3un-2.
u1 =3*2-2 = 4 ; u2 =3*4-2 = 10 ; u3 =3*10-2 = 28 ; réponse c.
3. Dans
un atelier 3% des pièces produites sont défectueuses. On constate qu’au
cours du contrôle qualité, si la pièce est bonne, elle est acceptée
dans 95% des cas, et que si elle est défectueuse, elle est refusée dans
98% des cas.
La probabilité qu’une pièce soit refusée est égale à :
0,0779 vrai ; 0,0294 ; 0,0485 ; 0,98.
Probabilité qu'une pièce soit refusée : 0,97 x 0,05 +0,03 x0,98 =0,0485 +0,0294=0,0779.
4. Sachant que cos x =5 / 13 et que x est compris entre −p/2 et 0, la valeur de sinx est :
8/13 ; -8/13 ; 12/13 ; -12 /13. vrai.
cos2 x +sin2x = 1 ; sin2 x = 1-25 /169 =(169-25) / 169 =144 / 169 ; sin x = ± 12 / 13.
x est compris entre −p/2 et 0, donc sin x = -12 / 13.
5. La loi de probabilité d’une variable aléatoire X est donnée par le tableau ci-dessous :
valeurs de xi
|
-2
|
0
|
5
|
pi = P(X = xi)
|
0,3
|
0,5
|
0,2
|
L’espérance E(X) de la variable aléatoire X est égale à : 3
E(x) = -2 x 0,3 +0 x 0,5 +5 x 0,2 = -0,6 +1 = 0,4. Réponse c.
|
|
Exercice 2. ( 5
points) Sujet 7.
Un
magasin de téléphonie mobile lance une offre sur ses smartphones de la
marque Pomme vendus à 800 € : il propose une assurance complémentaire
pour 50 € ainsi qu’une coque à 20 €. Ce magasin a fait les
constatations suivantes concernant les acheteurs de ce smartphone :
• 40% des acheteurs ont souscrit à l’assurance complémentaire.
• Parmi les acheteurs qui ont souscrit à l’assurance complémentaire, 20% ont acheté en plus la coque.
• Parmi les acheteurs qui n’ont pas souscrit à l’assurance complémentaire, deux sur trois n’ont pas acheté la coque.
On interroge au hasard un client de ce magasin ayant acheté un smartphone de la marque Pomme.
On considère les évènements suivants :
• A : « le client a souscrit à l’assurance complémentaire » ;
• C : « le client a acheté la coque ».
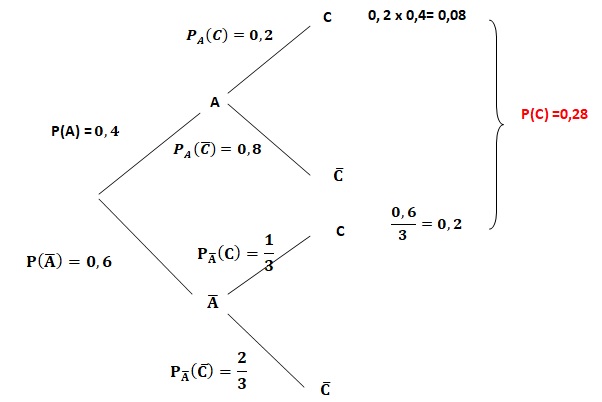
1. Calculer la probabilité que le client ait souscrit à l’assurance complémentaire et ait acheté la coque.
P(A n C) =0,2 x0,4 = 0,08.
2. Montrer que P(C) = 0,28.
3. Le client interrogé a acheté la coque.
Quelle est la probabilité qu’il n’ait pas souscrit à l’assurance complémentaire ?
PC non A =P (C n non A) / P(C) =0,2 / 0,28 =0,714.
4. Déterminer la dépense moyenne d’un client de ce magasin ayant acheté un smartphone de la marque Pomme.
On pourra noter X la variable aléatoire qui représente la dépense en
euros d’un client de ce magasin ayant acheté un smartphone de la marque
Pomme.
P(X =800+ 50+20) =P(X = 870) = 0,08.
P(X = 850) =0,4 x0,8 = 0,32.
P(X =820) = 0,2.
P(X =800)=0,6 x 2 /3 =0,4.
Dépense moyenne : 820 x 0,2 +850 x 0,32 + 870 x 0,08 +800 x0,4=4 +16 +5,6 =825,6 €.
Sujet 8.
En 2019, le nombre d’abonnés à une page de réseau social d’un musicien était de 6 000.
On suppose que chaque année, il obtient 750 abonnés supplémentaires.
On désigne par un le nombre d’abonnés en 2019+n pour tout entier naturel n.
1. Calculer le nombre d’abonnés en 2020 et 2021.
6750 en 2020 et 7500 en 2021.
2. Exprimer un+1 en fonction de un.
un+1 = un + 750.
3. Quelle est la nature de la suite (un) ?
C'est une suite arithmétique de raison 750 et de premier terme 6000.
4. En déduire une expression de un en fonction de n.
un = 6000 +750n.
5. En quelle année le nombre d’abonnés aura triplé par rapport à l’année 2019 ?
un = 18000 =6000 +750n ; 12000 = 750 n ; n =16 ( année 2019 +16 = 2035).
|
Exercice 3. ( 5
points). Sujet 7. On considère les deux suites suivantes :
• la suite (un) définie pour tout entier n par : un =(8n −4) / (n +1)
• la suite (vn) définie par v0 = 0 et vn+1 = 0,5vn +3,5 pour tout entier n.
1. Calculer les termes d’indice 3 des suites (un) et (vn).
u3 =(8*3-4) /(3+1) =0 / 4 = 5.
v1 =0,5v0 +3,5 =0,5 *0+3,5 = 3,5.
v2 =0,5v1 +3,5 =0,5 *3,5 +3,5 = 5,25.
v3 =0,5v2 +3,5 =0,5 *5,25 +3,5 = 6,125.
2. On s’intéresse aux variations de la suite (un). Pour cela, on considère la fonction f définie sur [0 ; +∞[ par :
f (x) =(8x −4) / (x +1).
a. Démontrer que la fonction f est croissante sur [0 ; +∞[.
Calcul de la dérivée f ' en posant u = 8x-4 et v = x+1 ; u' =8 ; v' = 1.
(u'v-v'u) / v2 =[8(x+1) -(8x-4] /(x+1)2 =12 /(x+1)2.
La dérivée étant positive, la fonction est strictement croissante.
b. En déduire la monotonie de la suite (un).
La fonction f étant strictement croissante, la suite (un) est monotone.
3. On considère l’affirmation suivante :
« pour tout entier n, un < vn ».
Camille pense que cette affirmation est vraie alors que Dominique pense le contraire.
Pour les départager, on réalise le programme suivant écrit en langage Python :
def algo( n= 0 :
u=-4
v= 0
while u < v
n = n+1
u = (8*n - 4)/(n + 1)
v = 0,5*v + 3,5
return(n)
Le programme renvoie la valeur 11. Qui de Camille ou Dominique a raison ? Expliquer.
D'après ce programme, un < vn tant que n est inférieur à 11. Si n est supérieur à 11, alors un > vn . Dominique a raison.
Sujet 8.
Un
médicament contre la douleur est administré par voie orale. La
concentration du produit actif dans le sang, en milligramme par litre
de sang, est modélisé par la fonction f qui, au temps écoulé
x en heure, x étant compris entre 0 et 6, associe :
f (x) = x3 −12x2 +36x où x appartient à [0 ; 6].
Le produit actif est efficace si sa concentration dans le sang est supérieure ou égale à 5 mg/L.
1. En exécutant le script Python ci-dessous, on obtient la liste [0, 1, 1, 1, 1, 1, 0].
1 liste=[0, 0, 0, 0, 0, 0, 0]
2 for x i range(0,7) :
3 if x**3-12*x**2+36*x>=5:
4 liste[x]= 1
5 print(liste)
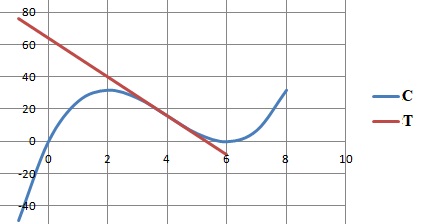
À l’aide de ce résultat, indiquer l’intervalle de temps en unité d’heures sur lequel le médicament est efficace.
Le médicament est efficace entre 1 heure et 5 heures après la prise.
2. On admet que la fonction f est dérivable sur l’intervalle [0; 6], calculer sa fonction dérivée.
f '(x) = 3x2 -24x +36.
3. Justifier que la
tangente T à la courbe représentative de la fonction f au point A
d’abscisse 4 admet pour équation réduite y = −12x +64.
Coefficient directeur de la tangente = f '(4) =3*16 -24*4+36= -12.
Ordonnée du point A : f(4) =43-12 *16 +36*4 =16.
Les coordonnées de A vérifient l'équation de la tangente : 16 = -12 *4 +b ; b = 64.
y = 12x +64.
4. Démontrer que f (x)−(−12x +64) = (x −4)3.
(x-4)(x-4)2 =(x-4)(x2-8x+16) =x3-8x2+16x-4x2+32x-64 =x3-12x2+48x-64.
f (x)−(−12x +64) =x3 −12x2 +36x +12x-64=x3-12x2+48x-64.
5. En déduire la position relative de la courbe représentative de la fonction par rapport à la tangente T au point A.
f (x)−(−12x +64) =(x −4)3 est négatif si x < 4 et positif si x > 4.
T est au dessus de la courbe reprentative de f si x < 4 et en dessous si x > 4.
|
Exercice4. ( 5 points) Sujet 7. Le plan est muni d’un repère orthonormé. La courbe représentative C d’une fonction f définie sur R est donnée ci-dessous :
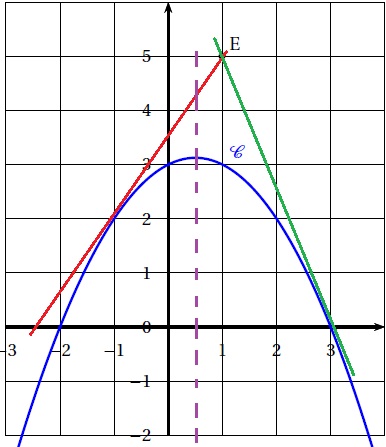
1. Par lecture graphique, résoudre l’équation f (x) = 0 d’inconnue x.
x = -2 et x = 3.
2. On donne f ′(x) = −x +0,5 pour tout réel x.
Déterminer qu’une équation de la tangente T à la courbe C au point d’abscisse −1 est y = 1,5x +3,5.
Equation de la tangente T = y = ax+b avec a = f '(-1) =-(-1)+0,5= 1,5.
Les coordonnées du point C (-1 ; 2) vérifient l'équation de T : 2 =1,5 *(-1) +b ; b = 3,5.
y = 1,5 x +3,5.
3. On considère le point E de coordonnées (1; 5).
Dans cette question, on cherche à déterminer les points de la courbe C en lesquels la tangente passe par le point E.
a. Montrer que le point E appartient à la tangente T .
5 =1,5 *1 +3,5 est bien vérifié ; E appartient à la tangente T.
b. Déterminer l’autre point de la courbe en lequel la tangente passe par le point E.
Equation de la tangente T ' : y=ax+b.
E (1 ; 5) appartient à T ' : 5 = a+b ; b = 5-a.
a = f '(x) = -x+0,5 ; y = (-x+0,5) x+5-(-x+0,5) =-x2+0,5x +5+x -0,5 = -x2 +1,5 x +4,5.
Equation de la courbe C : y = -0,5x2 +0,5x +3.
-0,5x2 +0,5x +3 = -x2 +1,5 x +4,5.
0,5x2 -x-1,5 = 0. Discriminant : 12-4*0,5*(-1,5) =4.
Solutions : x = (1+2) / (2 *0,5) =3 et x = (1-2) / (2 *0,5) =-1.
Les coordonnées de l’autre point de la courbe en lequel la tangente passe par le point E sont :
x = 3 et y = -0,5 *32+0,5 *3+3= 0..
|
Sujet 8.
Dans
le plan muni d’un repère orthonormé, on considère le point A de
coordonnées (3; 1) ainsi que la droite (d) d’équation cartésienne x −3y
−4 = 0.
1. Déterminer les coordonnées du point B d’abscisse 7 appartenant à la droite (d).
7 -3 y-4=0 ; y = 1.
2. Donner un vecteur normal à la droite (d).
Coordonnées d'un vecteur normal de la droite (d) : (1 ; -3).
3. Déterminer une équation de la droite (D) perpendiculaire à la droite (d) passant par le point A.
Coefficient directeur de cette droite : -3 ; y = -3x+b.
A (3 ; 1) appartient à cette droite : 1 =-3*3+b ; b =10 ; y = -3x +10.
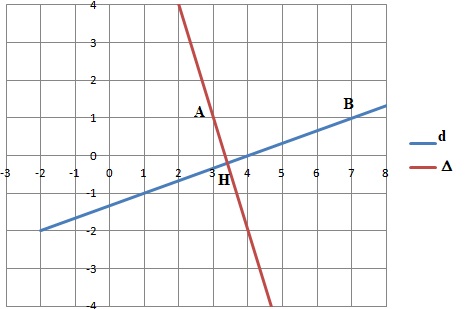
4. Calculer les coordonnées du projeté orthogonal H du point A sur la droite (d).
H est l'intersection des deux droites perpendiculaires.
yH = -3xH +10=xH /3-4 /3 ; 10 / 3 xH =34 /3 ; xH =3,4.
yH = -3,4 *3 +10 = -0,2.
5. Calculer la distance AH et en donner une interprétation.
AH =[ (3,4-3)2 +(-0,2 -1)2]½ =(0,16 +1,44)½ =1,6½ .
AH est la distance de A à la droite d.
|
|