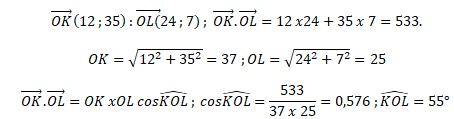Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujets 9
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée)
1.
On choisit au hasard un individu parmi les passagers en transit dans un
aéroport. On a représenté ci-dessous un arbre de probabilités lié à
certains évènements dont certains éléments ont été effacés.
On considère les évènements suivants :
— A : « le passager parle anglais »
— B : « le passager ne parle pas anglais »
— E : « le passager est un membre de l’Union Européenne »
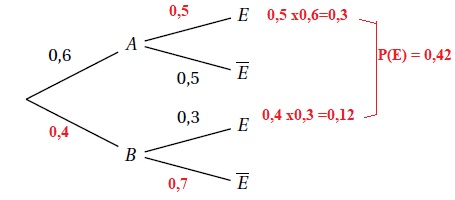
Réponse B : p(E) = 0,42.
2. Le plan est muni d’un repère orthonormé. Soit D la droite d’équation 3x + y −2 = 0.
a. Le point de coordonnées (6 ; −15) appartient à D. Faux.
3*6-15 -2= 1, différe de zéro.
b. D est perpendiculaire à la droite d’équation 12x +4y = 0. Faux.
y = -3x+2 coefficient directeur : -3.
y = -3 x coefficient directeur -3. ces droites sont parallèles.
c. Le vecteur de coordonnées (1; 3) est un vecteur directeur de D. Faux.
Coordonnées d'un vecteur directeur de D : ( 1 ; -3).
d. Le vecteur de coordonnées (3; 1) est un vecteur directeur des droites perpendiculaires à D. Vrai.
3. On considère dans l’ensemble des réels l’équation trigonométrique sin x = 1.
a. Cette équation admet une unique solution dans l’ensemble des réels. Faux ( x = p/2 + 2kp avec k nombre entier relatif )
b. Cette équation admet une infinité de solutions dans l’ensemble des réels. Vrai.
c. 2π est une solution de cette équation. Faux.
d. − 57π / 2 est une solution de cette équation. Faux.
-57 p /2 = -58 p /2 +p/2=-29 p +p/2 différe de p/2 + 2kp.
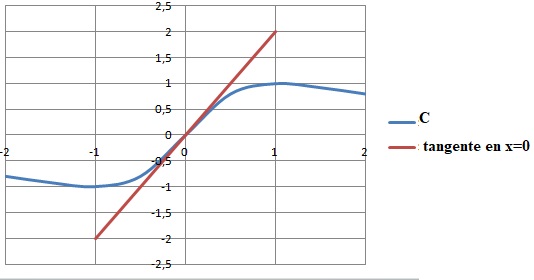
4. Soit f la fonction définie sur l’ensemble des nombres réels par f (x) =2x /(x2 +1) et C sa courbe représentative dans un repère du plan.
a. La courbe C n’admet pas de tangente au point d’abscisse 0
b. La tangente à C au point d’abscisse 0 pour équation y = 2x. Vrai.
c. La tangente à C au point d’abscisse 0 a pour coefficient directeur 1
d. La tangente à C au point d’abscisse 0 est parallèle à l’axe des abscisses.
Calcul de la dérivée en posant u = 2x et v = x2+1 ; u' = 2 ; v' = 2x.
(u'v-v'u) / v2 =[2(x2+1)-4x2] / (x2+1)2 =2(-2x2+1) / (x2+1)2 .
f '(0) = 2.
Equation de la tangente en x = 0 : y = 2x.
5. Soit la fonction f définie sur l’intervalle ]−2 ; +∞[ par : f (x) =(x −3) / (x +2)
f est dérivable sur l’intervalle ]−2 ; +∞[ et pour tout réel x de ]−2 ; +∞[, la dérivée est :
On pose u = x-3 et v = x+2 ; u' =v' = 1.
(u'v-v'u) / v2 =(x+2-(x-3)) /(x+2)2 = 5 /(x+2)2 . Réponse c.
.
Sujet 10.
1. Lors d’une même expérience aléatoire, deux évènements A et B vérifient :
P(A) = 0,4 ; P(B) = 0,6 ; P(A∩ non B) = 0,3.
Alors :
a. P(A∩B) = 0,1 vrai ; b. P(A∩B) = 0,24 ; c. P(A∪B) = 1 ; d. P(A∪B) = 0,7.
Formule des probabilités totales : P(A) =P(A ∩ B) + P(A ∩ non B) ;
0,4 = P(A ∩ B) + 0,3 ; P(A ∩ B) =0,1.
2. On considère la fonction f définie sur R par f (x) = x2 −3x +4. L’abscisse duminimum de f est :
a. -1,5 ; b. 2 /3 ; c. 1,5 vrai ; d. 1.
f '(x) = 2x-3 ; f '(x) = 0 si x = 1,5.
Le coefficient a de la fonction du second degré étant positif, il s'agit d'un minimum.
3. Soit (un) une suite arithmétique telle que u5 = 26 et u9 = 8. La raison de (un) vaut :
a. −18 ; b. 8 / 26 ; c. 4,5 ; d. −4,5 vrai.
u9-u5 = 4 r ; 8-26 = 4 r ; r = -4,5.
4. On considère l’algorithme suivant, écrit en langage usuel :
Suite(N)
A←10
Pour k de 1 à N
A 2*A-4
Fin Pour
Renvoyer A
Pour la valeur N = 4 le résultat affiché sera :
a. 4 ; b. 100 vrai ; c. 52 ; d. 196.
Pour k = 1, A =16 ; pour k = 2, A =28 ; pour k = 3, A =52 ; pour k = 4, A =100.
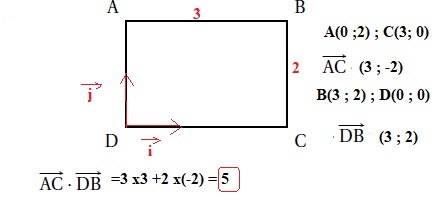
5. On considère un rectangle ABCD tel que AB = 3 et AD = 2.
Alors le produit scalaire suivant vaut :
a. 0 ; b. 5 vrai ; c. 6 ; d. −6.
|
|
Exercice 2. ( 5
points) Sujet 9. À
la naissance de Lisa, sa grand-mère a placé la somme de 5 000 euros sur
un compte et cet argent est resté bloqué pendant 18 ans.
Lisa retrouve dans les papiers de sa grand-mère l’offre de la banque :
Offre :
Intérêts composés au taux annuel constant de 3%.
À la fin de chaque année le capital produit 3% d’intérêts qui sont intégrés au capital.
On considère que l’évolution du capital acquis, en euro, peut être modélisée par une suite (un) dans laquelle, pour tout entier naturel n, un est le capital acquis, en euro, n années après la
naissance de Lisa.
On a ainsi u0 = 5000.
1. Montrer que u1 = 5150 et u2 = 5304,5.
u1 = 5000 x1,03 =5150 ; u2 = 5150 x1,03 =5304,5.
2. a. Pour tout entier naturel n, exprimer un+1 en fonction de un.
En déduire la nature de la suite (un) en précisant sa raison et son premier terme.
Suite géométrique de raison 1,03 et de premier terme u0 = 5000.
un+1 = 1,03un.
b. Pour tout entier naturel n, exprimer un en fonction de n.
un = 5000 x 1,03n.
3. Calculer le capital acquis par Lisa à l’âge de 18 ans. Arrondir au centième.
u18 = 5000 x 1,0318 =8512,17 €.
4. Si Lisa n’utilise pas le capital dès ses 18 ans, quel âge aura-t-elle quand celui- ci dépassera 10 000 euros ?
5000 x 1,03n > 10 000 ; 1,03n > 2 ; n > ln(2) / ln(1,03) ; n >23,44 ; n > 24. (24 ans).
Sujet 10.
Un
industriel souhaite fabriquer une boîte sans couvercle à partir d’une
plaque de métal de 18 cm de largeur et de 24 cm de longueur. Pour cela,
il enlève des carrés dont la longueur du côté mesure x cm aux quatre
coins de la pièce d emétal et relève ensuite verticalement pour fermer
les côtés.
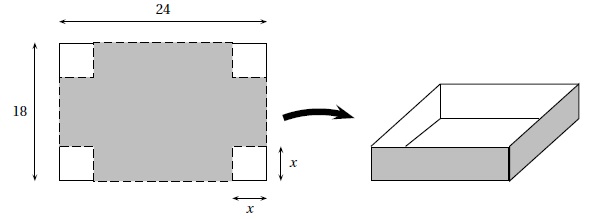
Le volume de la boîte ainsi obtenue est une fonction définie sur l’intervalle [0; 9] notée V (x).
1. Justifier que pour tout réel x appartenant à [0; 9] : V (x) = 4x3 −84x2 +432x.
Largeur : 18-2x ; longueur 24-2x ; hauteur x.
V = (18-2x) (24-2x) x = (432 -36x -48+4x2) x =(432 -84 x +4x2) x =4x3 −84x2 +432x.
2. On note V ′ la fonction dérivée de V sur [0; 9]. Donner l’expression de V ′(x) en fonction de x.
V'(x) =12x2 -168x+432 = 12 (x2-14x+36).
Solutions de x2-14x+36=0 ; discriminant : 142 -36*4= 52.
Valeur retenue :(14 -2 *13½) / 2 =7 -13½~3,4.
V'(x) >0 si 0 < x < 3,4 et V(x) croissante ; V'(x) < 0 si 3,4 < x < 9 et V(x) décroissante.
3. Dresser alors le tableau de variations de V en détaillant la démarche.
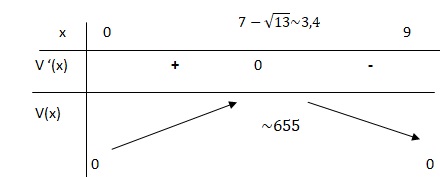
4. Pour quelle(s) valeur(s) de x la contenance de la boîte est-elle maximale ?
V est maxi pour x ~3,4.
5. L’industriel peut-il construire ainsi une boîte dont la contenance est supérieure ou égale à 650 cm3 ? Justifier.
650 < 655, donc l'industriel peut construire une boîte de contenance supérieure à 650 cm3.
|
Exercice 3. ( 5
points). Sujet 9. Le rectangle OABC ci-dessous représente une place touristique vue de dessus. Le plan est muni d’un repère orthonormé.
Afin d’éclairer le plus grand nombre demonuments, on place au point O,
un projecteur lumineux qui permet d’éclairer la partie du plan
délimitée par les segments de droite [OK] et [OL] tels que
K est le milieu de [AB] et
1. Déterminer par lecture graphique les coordonnées des points A, B, C, K et L.
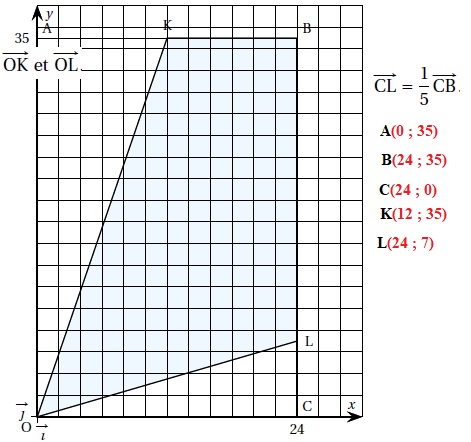
2. Un visiteur affirme : «Moins de 70% de la surface de la place est éclairée ». Cette affirmation est-elle exacte?
Aire du trapèze OCBK : (24 +12) *35 /2 =630 m2.
Aire du triangle OCL : 24 *7 /2 =84 m2.
Aire éclairée : 630-84 =546 m2.
Aire du rectangle OABC : 24 x35 = 840 m2.
546 / 840 =0,65 (65 %). L'affirmation est exacte.
3. a. Donner les coordonnées des vecteurs suivants :
b. Montrer que leur produit scalaire est égal à 533.
c. En déduire la mesure, arrondie au degré, de l’angle formé par ces 2 vecteurs.
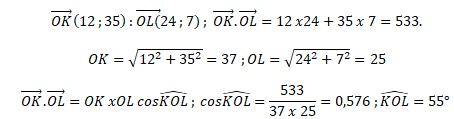
Sujet 10.
Une
angine peut être provoquée soit par une bactérie (angine bactérienne)
soit par un virus (angine virale). On admet qu’un malade ne peut pas
être à la fois porteur du virus et de la bactérie.
L’angine est bactérienne dans 20% des cas.
Pour déterminer si une angine est bactérienne, on dispose d’un test. Le
résultat du test peut être positif ou négatif. Le test est conçu pour
être positif lorsque l’angine est bactérienne mais il présente
des risques d’erreur :
• si l’angine est bactérienne, le test est négatif dans 30% des cas
• si l’angine est virale, le test est positif dans 10% des cas
On choisit au hasard un malade atteint d’angine. On note :
• B l’évènement : « l’angine est bactérienne » ;
• T l’évènement : « le test effectué sur le malade est positif ».
Si besoin, les résultats seront arrondis à 10−3 près.
1. Représenter la situation par un arbre pondéré.
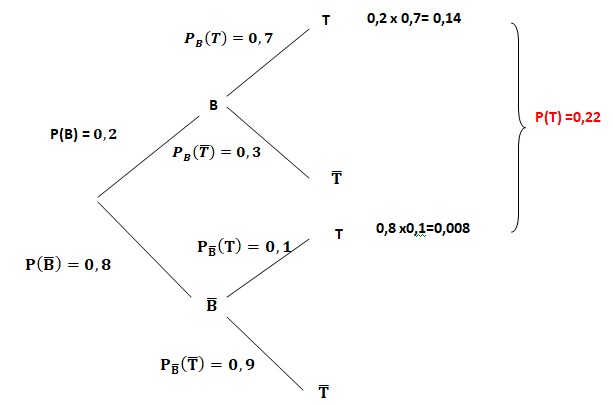
2. Quelle est la probabilité que l’angine soit bactérienne et que le test soit positif ?
P(B n T) = 0,2 x0,7 = 0,14.
3. Montrer que la probabilité que le test soit positif est 0,22.
Formule des probabilités totale : P(T) =P(B n T) +P(non B n T)=0,14 +0,8 x0,1 = 0,14 +0,08 = 0,22.
4. Un malade est choisi
au hasard parmi ceux dont le test est positif. Quelle est la
probabilité pour que son angine soit bactérienne?
PT(B) = P (B n T) / P(T) =0,14 / 0,22 ~0,636.
|
Exercice4. ( 5 points) Sujet 9. On considère la fonction f définie et dérivable sur l’intervalle [0 ; +∞[ par [(x) =x3 -x2 -x-1.
1. On note f ′ la fonction dérivée de f .
a. Montrer que, pour tout réel x, f ′(x) = 3(x+1/3)(x-1).
f '(x) = 3x2-2x-1.
3(x+1/3)(x-1) =(3x+1)(x-1) =3x2-3x+x-1 =3x2-2x-1= f '(x)
b. En déduire le tableau de variation de f sur [0 ; +∞[.
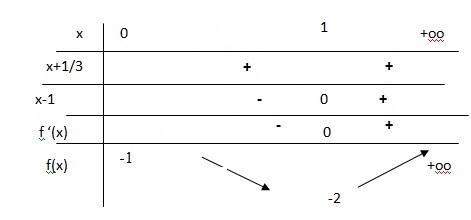
c. Déterminer l’abscisse du point de la courbe représentative de f pour lequel le coefficient directeur de la tangente vaut 7.
f '(x) = 7 ; 3x2-2x-1 = 7 ; 3x2-2x-8 =0.
Discriminant : 22 +4*8*3=100;solution retenue : x = (2 +10)/6 = 2.
2. On note x0 l’unique solution de l’équation f (x) = 0. On admet que x0 ∈ [1 ; 2].
On considère la fonction suivante définie en langage Python.
def zero_de_f(n) :
a = 1
b = 2
for k in range(n) :
x = (a + b)/2
if x∗∗3 - x∗∗2- x - 1 < 0 :
a = x
else :
b = x
return a, b
a. On applique
cette fonction pour n = 3. Reproduire sur la copie et compléter le
tableau suivant, jusqu’à l’arrêt de l’algorithme.
itération
|
x = (a+b) / 2
|
f(x) < 0 ?
|
a
|
b
|
amplitude de [a ; b]
|
k=0
|
1,5
|
oui
|
1,5
|
2
|
0,5
|
k=1
|
1,75
|
oui
|
1,75
|
2
|
0,25
|
k=2
|
1,875
|
non
|
1,75
|
2
|
0,25
|
b. En déduire un encadrement de x0, d’amplitude 0,125, par deux nombres décimaux.
1,75 < x0 < 1,875
|
Sujet 10.
Un
service de vidéos à la demande réfléchit au lancement d’une nouvelle
série mise en ligne chaque semaine et qui aurait comme sujet le
quotidien de jeunes gens favorisés.
Le nombre de visionnages estimé la première semaine est de 120 000. Ce nombre augmenterait ensuite de 2% chaque semaine.
Les dirigeants souhaiteraient obtenir au moins 400 000 visionnages par semaine.
On modélise cette situation par une suite (un) où un représente le nombre de visionnages n semaines après le début de la diffusion. On a donc u0 = 120000.
1. Calculer le nombre u1 de visionnages une semaine après le début de la diffusion.
u1 =120 000 x1,02 =122 400.
2. Justifier que pour tout entier naturel n : un = 120000×1,02n .
La suite est géométrique de premier terme u0 = 120 000 et de raison q = 1,02.
3. À partir de combien de semaines le nombre de visionnages hebdomadaire sera-t-il supérieur à 150 000 ?
120000×1,02n > 150 000 ; 1,02n > 15 /12 ; n ln(1,02) > ln(15 /12) ; n > 11,27 soit n > 12.
Au bout de 12 semaines le nombre de visionnages dépasse 150 000.
4. Voici un algorithme écrit en langage Python :
def seuil():
u=120000
n=0
while u<400000:
n=n+1
u=1.02*u
return n
Déterminer la valeur affichée par cet algorithme et interpréter le résultat précédent dans le contexte de l’exercice.
L'algorithme affiche au bout de combien de semaines le nombre de visionnage dépasse 400 000.
120000×1,02n > 400 000 ; 1,02n > 40 /12 ; n ln(1,02) > ln(40 /12) ; n > 60,8 soit n > 6112.
Au bout de 61 semaines le nombre de visionnages dépasse 400 000.
5. On pose pour tout entier naturel n : Sn = u0 +. . .+un. Montrer quel’on a :
Sn = 6 000 000×(1,02n+1 −1) .
Somme de n termes d'une suite géométrique de premier terme 120 000 et de raison q = 1,02.
S = 120 000 (1-1,02n+1) / (1-1,02)=120 000 (1-1,02n+1) / (-0,02 )=6 000 000×(1,02n+1 −1) .
En déduire le nombre total de visionnages au bout de 52 semaines (arrondir à l’unité).
S52 = 6 000 000×(1,0253 −1)~1,114 107.
|
|