Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 17
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. On considère la loi de probabilité de la variable aléatoire X donnée par le tableau ci- dessous :
k
|
-5
|
0
|
10
|
20
|
50
|
P(X=k)
|
0,71
|
0,03
|
0,01
|
0,05
|
0,2
|
L’espérance de X est :
a) 15 ; b) 0,2 ; c) 7,55 ; d) 17.
E(X) = -5*0,71 +0 +10*0,01+20*0,05+50*0,2 =7,55. Réponse c.
2.On se place dans un repère orthonormé.
Le cercle de centre A( -2 ; 4) et de rayon 9 a pour équation :
a) (x+2)2+(y−4)2=81 vrai
b) (x−2)2+(y+4)2=81
c) (x+2)2+(y−4)2=9
d) (x−2)2+(y+4)2=9
3. Soit 𝑓 la fonction définie par f(x) =ax2 +bx+c où a, b, c sont des réels.
On considère dans un repère la courbe représentative de f tracée ci dessous. On appelle Δ son discriminant.
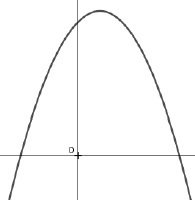
On peut affirmer que :
a) a>0 ou c <0
b) c et Δ sont du même signe. vrai.
c) a <0 et c <0
d) a<0 et Δ<0.
La parabole présente un maximum, donc a <0.
La parabole coupe l'axe des abscisses en deux points, donc D >0.
La parabole coupe l'axe des ordonnées en c >0.
4. On considère la suite (un) définie par u0=−2 et un+1=2un−5.
Un algorithme permettant de calculer la somme S = u0+ u1+⋯+u36 est :

Réponse d.
5. La suite (un) définie par u0=−2 et un+1=2un−5 est :
a) arithmétique mais pas géométrique
b) géométrique mais pas arithmétique
c) ni arithmétique, ni géométrique. vrai.
d) à la fois arithmétique et géométrique
un+1-un=un−5 n'est pas une constante : la suite n'est pas arithmétique.
un+1/un=2-5/un n'est pas une constante : la suite n'est pas géométique.
Sujet 18.
1. Soit P une probabilité sur un univers Ω et 𝐴 et 𝐵 deux évènements indépendants tels que P(A)=0,5 et P(B)=0,2.
Alors P(A u B) est égal à :
a) 0,1 ; b) 0,7 ; c) 0,6 vrai ; d) On ne peut pas savoir..
P(A u B) = P(A)+P(B)-P(A n B) =0,5 +0,2 -0,5 x0,2 =0,6.
2. La valeur arrondie au centième de 1+1,2+1,22+1,23+⋯+1,210 est :
a) 3,27 ; b) 25,96; c) 26,96 ; d) 32,15 vrai.
Somme des 11 premiers termes d'une suite géométrique de premier terme 1 et de raison 1,2.
S = (1-1,211) / (1-1,2) =32,15.
réponse b.
3. Soit f la fonction définie sur R par 𝑓(𝑥)=x /ex.
Pour tout réel x ,f(x) est égal à :
a) 𝑓(𝑥)= e−𝑥/ (−𝑥) ; b) 𝑓(𝑥)=xe-x vrai ; c) f(x)= −xe−x d) f(x)= e-x / x.
4. Soit g la fonction définie sur R par g(x)=(2x−5)ex. On admet que g est dérivable sur R et on note g’ sa fonction dérivée.
Alors pour tout réel x , g'(x) est égal à :
a) (2x−3)ex vrai; b) (−2x+7)ex ; c) 2ex d) −5ex.
On pose u = 2x-5 et v = ex ; u' = 2 ; v' = ex.
u'v +v'u = 2ex+ex(2x-5)=ex(2x-3).
5. Le nombre e 3×e−5/ e2 est égal à :
a) −1 ; b) e−7,5 ; c) 1/e4 vrai ; d) 1,5 e−5.
exp(3-5-2) =exp(-4) = 1 / e4.
|
|
Exercice 2. ( 5
points) Sujet 17. La fonction f est définie sur]−1;+∞[ par : f(x)=(x2+1) / (x+1)
On se place dans un repère orthonormé du plan.
Démontrer que pour tout x appartenant à l’intervalle ]−1;+∞[:
f '(x) =(x2+2x-1) / ((x+1)2.
On pose u = x2+1 et v = x+1 ; u' = 2x ; v' = 1.
(u'v-v'u) / v2 =[(2x(x+1)-(x2+1) ] / (x+1)2=(x2+2x-1) / (x+1)2 .
2) Déterminer le sens de variation de la fonction f sur ]−1;+∞[.
Le dénominateur est toujours positif.
x2+2x-1=0 ; discriminant : 22-4*(-1) =8 = ( 2*2½)2.
Solutions : (-2 ±2*2½) / 2 = -1 ±2½ ; solution retenue x =-1 +2½.
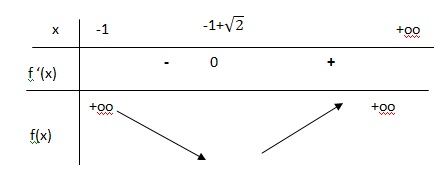
3) Déterminer une équation de la tangente T à la courbe représentative de f au point d’abscisse 0.
Coefficient directeur de T en x=0 : f '(0) = -1.
Equation de T : y = -x+b.
Le point de coordonnées (0 ; f(0) =1) appartient à T : 1 = b. y = -x+1.
4) Etudier la position relative de la courbe représentative de f et de la droite d’équation y=x.
On étudie la signe de f(x)-x= (x2+1) / (x+1) -x =[(x2+1)-x(x+1)] / (x+1) =(1-x) /( x+1).
x+1 est positif ; si x < 1, f(x)-x >0, f(x) au dessus de x.
si x >1, f(x)-x < 0, f(x) en dessous de x.
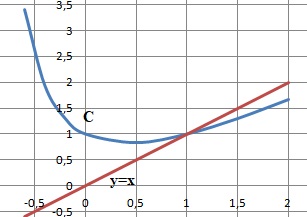
Sujet 18.
Une
banque propose un placement. Le compte est rémunéré et rapporte 5 % par
an. La banque prend des frais de gestion qui se montent à 12 euros par
an.
Ainsi, chaque année la somme sur le compte augmente de 5 % puis la banque prélève 12 euros.
Noémie place la somme de 1000 euros dans cette banque.
On appelle un la somme disponible sur le compte en banque de Noémie après n années, où n désigne un entier naturel.
On a donc u0=1000 et pour tout entier naturel n , un+1=1,05 un−12
1. Avec un tableur on a calculé les premiers termes de la suite (un) :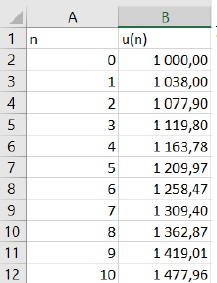
a. Quelle formule a-t-on entrée dans la cellule B3 avant de l’étirer pour obtenir ces résultats ?
=B2*1,05-12
b. En utilisant les
valeurs calculées de la suite, indiquer à Noémie combien de temps elle
doit attendre pour que son placement lui rapporte 20 %.
1000 x1,2 =1200. Elle doit attendre 5 ans.
On pose (vn) la suite définie, pour tout entier naturel n, par vn=un−240.
2. Montrer que la suite (vn) est géométrique de raison 1,05.
vn+1=un+1−240 =1,05 un−12-240=1,05(un-240) =1,05 vn.
vn+1 / vn = 1,05 , suite géométrique de raison 1,05.
3. Exprimer vn puis un en fonction de l’entier n.
vn = v0*1,05n =(1000-240)1,05n =760* 1,05n .
un =vn +240 =760* 1,05n +240.
4. Calculer à partir de cette dernière formule la somme disponible sur le compte en banque de Noémie après 20 ans de placement.
u20=760*1,0520+240=2256,51 €.
|
|
Exercice 3. ( 5 points).
Sujet 17.
Un jeu consiste à combattre en duel soit un monstre A, soit un monstre B.
On a une probabilité de 0,8 d’affronter le monstre A.
Le joueur gagne contre le monstre A dans 30% des cas, et gagne contre le monstre B dans 25% des cas.
Le joueur lance une partie. On considère les événements :
A :« Le joueur affronte le monstre A. »
B :« Le joueur affronte le monstre B. »
V :« Le joueur est victorieux. »
1) Déterminer PB(V̅) et interpréter le résultat.
La probabilité de perdre sachant que l'on a joué contre B est égale à 0,75.
2) Montrer que P(B∩V)=0,05.
0,2 x0,25 = 0,05.
3) Calculer P(V).
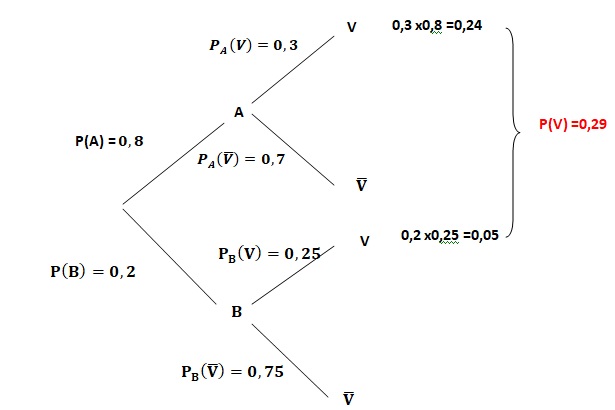
4) Calculer la probabilité d’avoir combattu le monstre B sachant que le joueur est victorieux.
PV(B) = P(V n B) / P(V) =0,05 /0,29 = 5 / 29.
Sujet 18.
Dans cet exercice toutes les probabilités seront données sous forme décimale, arrondie au millième.
Une entreprise récupère des smartphones endommagés, les répare et les reconditionne afin de les revendre à prix réduit.
45 % des smartphones qu’elle récupère ont un écran cassé ;
parmi les smartphones ayant un écran cassé, 30 % ont également une batterie défectueuse ;
par contre, seulement 20 % des smartphones ayant un écran non cassé ont une batterie défectueuse.
1.
Un technicien chargé de réparer et reconditionner les smartphones de
l’entreprise prend un smartphone au hasard dans le stock. On note :
E l’événement : « Le smartphone choisi a un écran cassé. »
B l’événement : « Le smartphone choisi a une batterie défectueuse. »
a. Représenter la situation décrite ci-dessus par un arbre pondéré.
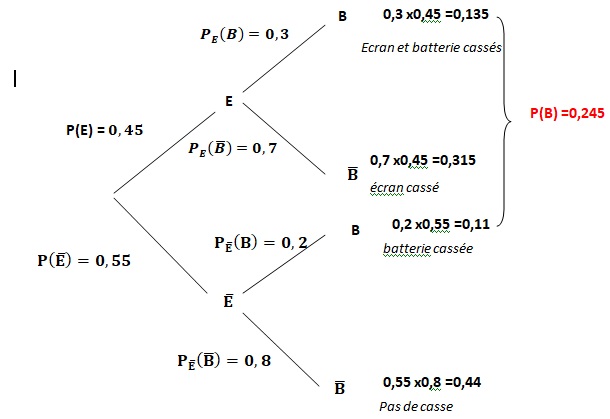
b. Démontrer que la probabilité que le smartphone choisi ait une batterie défectueuse est égale à 0,245.
P(E n B) + P(non E n B) =0,45 x0,3 +0,55 x0,2 =0,135 +0,110=0,245.
c. Sachant que le smartphone choisi a une batterie défectueuse, quelle est la probabilité qu’il ait un écran cassé ?
P B(E)=P(E n B) / P(B) = 0,3 x 0,45 / 0,245 =0,551.
2. L’entreprise
dépense 20 € pour réparer et reconditionner chaque smartphone qu’elle
récupère. Si l’écran est cassé, elle dépense 30 € supplémentaires, et
si la batterie est défectueuse, elle dépense 40 € supplémentaires.
On note X la variable aléatoire
égale au coût total de réparation et reconditionnement d’un smartphone
choisi au hasard dans le stock.
a.
Recopier et compléter sur la copie (aucune justification n’est
attendue) le tableau suivant pour donner la loi de probabilité de la
variable aléatoire X.
b. L’entreprise doit réparer et reconditionner 50
xi
|
20
|
50
|
60
|
90
|
P(X=xi)
|
0,44
|
0,315
|
0,11
|
0,135
|
b. L’entreprise doit réparer et reconditionner 500 smartphones. Combien doit-elle s’attendre à dépenser ?
E(X) =20*0,44 +50*0,315 +60*0,11 +90* 0,135=43,3 €.
500 x43,3 =21 650 €.
|
|
Exercice4. ( 5 points) Sujet 17 OABC et ODEF sont des carrés de côtés respectifs 3 et 2. OAMF est un rectangle.
On note H le projeté orthogonal du point Msur la droite (DC).
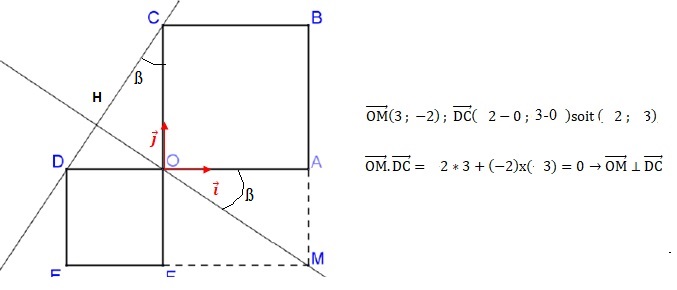
1) La droite (OM) est elle perpendiculaire à la droite (DC) ?
H étant le projeté orthogonal de M sur la droite (DC), les droites (OM) et (DC) sont perpendiculaires.
2) Calculer le produit scalaire suivant :
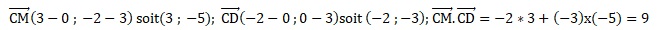
3) Déterminer la longueur CH.
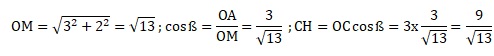
|
Sujet 18.
On donne ci-dessous les représentations graphiques respectives Cf et Cg de deux fonctions f et g définies sur R l’ensemble des nombres réels.
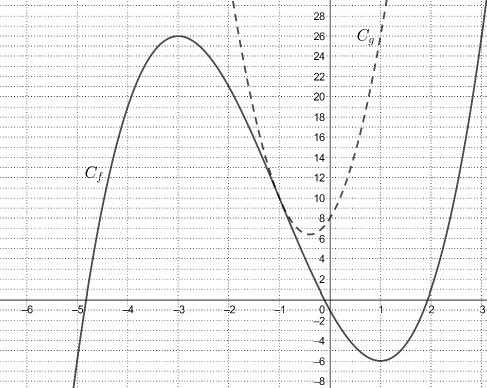
1. La fonction f est définie sur R par f(x))=x3+3x2−9x−1.
On admet qu’elle est dérivable sur R et on note f 'sa fonction dérivée.
a. Calculer f ′(x).
f '(x) =3x2+6x-9 = 3(x2+2x-3).
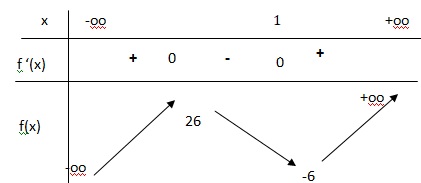
b. Déterminer le signe de f '(x) en fonction du réel x . En déduire le tableau de variation de la fonction f .
x2+2x-3 =0 ; discriminant : 22-3 *(-4) =16 = 42.
Solutions : (-2 ±4) / 2 =-1±2 soit -3 et 1.
f '(x) < 0 sur ]-3 ; 1[ et f est strictement décroissante.
f '(x) >0 sur ]-oo ; -3 [ et ]1 ; +oo[. ; f est strictement croissante
Pour x = -3, f présente un maximum et pour x = 1, f présente un minimum.
c. Déterminer une équation de la droite T tangente à Cf au point d’abscisse −1.
Coefficient directeur de T en x = -1 : f '(-1) =-12.
f(-1)=10 ; le point de coordonnées (-1 ; 10) appartient à T : 10 =-12*(-1) +b ; b =-2.
y = -12x-2. .
2. La fonction g est une fonction polynôme du second degré, il existe donc trois réels a, b et c tels que : g(x) = ax2 +bx+c pour tout réel x . On note Δ son discriminant.
a. Déterminer, à l’aide du graphique, le signe de a et le signe de Δ .
La parabole présente un minimum, a >0 ; la parabole ne coupe pas l'axe des abscisses, D < 0.
b. La fonction g est définie, pour tout réel x, par g(x)=10x2+8x+8.
Démontrer que les courbes Cf et Cg ont un point commun d’abscisse −1 et qu’en ce point elles ont la même tangente.
x3+3x2−9x−1=10x2+8x+8.
x3-7x2−17x−9=0, cette égalité est vérifiée pour x = -1.
Ordonnée de ce point : 10*(-1)2 +8(-1)+8=10.
Equation de la tangente T à Cf en x = -1 : y = -12x-1
Coefficient directeur de la tangente à Cg en x = -1 : g'(x)=20x+8 ; g'(-1) =-12.
Le point (-1 ; 10) appartient à cette tangente : 10 = -12*(-1) +b ; b = -2.
y = -12x-2, il s'agit de T.
.
|
|