Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 21
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. (un) est la suite arithmétique telle que u4 = 3 et u10 = 18. On peut affirmer que :
a) u0 = 7 ; b) u7 = 20,5 ; c) u12 = 23 ; d) u14 = −28.
u10-u4 = 18-3 = 15 = 6 r = r = 2,5.
u0 = u4-4 r =3-10=-7 ; u7 = -7 +7*2,5 = 10,5 ; u12 = -7 +12*2,5 =23. Réponse c.
2. 2 + 3 + 4 + ⋯ + 999 + 1000 est égal à :
a) 500 500 ; b) 498 999 ; c) 499 000 ; d) 500 499.
Suite arithmétique de raison 1 et de premier terme 2.
Somme des 999 premiers termes S =999 (2+1000) / 2 = 500 499. Réponse d.
3. (vn) est la suite géométrique de raison 0,3 telle que v0 = −3. On conjecture que la suite (vn) a pour limite :
a) 0; b) +∞ ; c) −∞ ; d) −3.
vn = v0 x 0,3n = -3x 0,3n ; quand n tend vers plus l'infini, 0,3n tend vers zéro. Réponse a.
4. f est la fonction définie sur ℝ par f(x) = −2(x + 2)2 − 3. On peut affirmer qu’elle est :
a) décroissante sur ]−∞ ; +∞[
b) décroissante sur ]−2 ; +∞[
c) croissante sur ]−∞ ; 2[
d) décroissante sur ]−3 ; +∞[.
f '(x) = -4(x+2) ; f '(x) = 0 pour x = -2. f '(x) > 0 pour x < -2 et f(x) est croissante.
f '(x) < 0 pour x > -2 et f(x) décroissante. Réponse b.
5. L’ensemble des solutions de l’inéquation x2 − 5𝑥 + 6 < 0 est
a) ]−∞; 2[ ∪ ]3; +∞[ ; b) ]−∞; −1[ ∪ ]6; +∞[ ; c) ]2 ; 3[ ; d) ]−1 ; 6[
Solutions de x2 − 5𝑥 + 6=0 ; discriminant : (-5)2-4*6=1.
solutions : x = (5 ±1) / 2 soit 3 et 2.
Le coefficient a=1 étant positif, x2 − 5𝑥 + 6 < 0 pour x compris entre 2 et 3. Réponse c.
Sujet 22.
1.
Sur la figure ci-dessous, nous avons tracé dans un repère orthonormé la
courbe représentative C d’une fonction f dérivable sur R et la tangente
à C au point d’abscisse 4. Cette tangente est représentée par la droite
D . On note f ' la fonction dérivée de la fonction f .
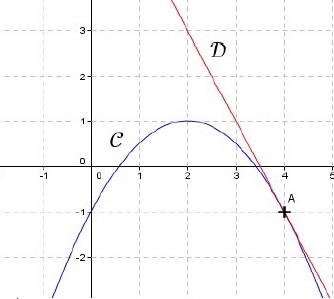
Le réel f '(4) est égal à : a) −1 ; b) −2 ; c) 7 ; d) 1.
Coefficient de la tangent D : f '(4) = -2, d'après le graphe. Réponse b.
2. Soit f la fonction définie sur R par f(x)=x3−2x2+1. On admet que f est une fonction
dérivable sur R. Dans un repère, une équation de la tangente à la
courbe représentative de la fonction f au point d’abscisse 1 est :
a) y=−1 ; b) y = -x ; c) y = -x+1 ; d) y =x.
Coefficient directeur de la tangente en x = 1 : f '(x) = 3x2 -4x ; f '(1) =3-4 = -1.
Le point de coordonnées x=1 ; f(1) =0 appartient à cette tangente.
Equation de la tangente : 0 = -1+b, b =1 ; y = -x+1. Réponse c.
3. Pour tout réel x , ex *e-3x / e-x est égal à :
a) e−x ; b) e3x ; c) e−3x ; d) ex.
ex-3x-(-x)=e-x. Réponse a.
4. Soit f une fonction polynôme du second degré dont la courbe représentative dans un repère orthonormé est donnée ci-dessous.
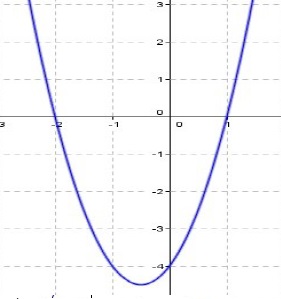
Pour tout réel x, une expression de f(x) est :
a) f(x)=x2+x−2 ; b) f(x)=−x2−4 ; c) f(x)=2x2+2x−4 ; d) f(x)=−3x2−3x+6.
f(x)=ax2 +bx +c ; f(0) = -4 = c ; f(1)=0=a+b-4 ; a+b = 4 (1) ;
f(-2) =0 =4a -2b -4 ; 2a-b-2=0 ; b =2a-2 ; repport dans (1) : a+2a-2 =4 ; a =2 ; b =2.
f(x) = 2x2+2x-4. Réponse c.
5. L’ensemble S des solutions de l’inéquation d’inconnue x réel : −x2−2x+8 > 0 est :
a) S=[−4 ; 2] ; b) S=]−4 ; 2[ ; c) S=]−∞;−4]∪]2;+∞[ ; d) S={−4 ; 2} .
Solutions de −x2−2x+8 =0 ; x2 +2x-8 =0.
Discriminant :22+4*8=36 = 62 ; x =(-2 ±6) / 2 soit 2 et -4.
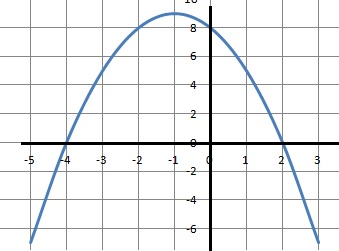
Réponse b.
|
|
Exercice 2. ( 5
points) Sujet 21. Une entreprise fabrique des pièces en acier, toutes identiques, pour l’industrie aéronautique.
Ces pièces sont coulées dans des moules à la sortie du four. Elles sont
stockées dans un entrepôt dont la température ambiante est maintenue à
25°C.
Ces pièces peuvent être modelées dès que leur température devient
inférieure ou égale à 600°C et on peut les travailler tant que leur
température reste supérieure ou égale à 500°C. La température de ces
pièces varie en fonction du temps.
On admet que la température en degré Celsius de ces pièces peut être
modélisée par la fonction f définie sur l’intervalle [0 ; +∞[ par :
f(t)=1375e−0,075 t+25, où t correspond au temps, exprimé en heures, mesuré après la sortie du four.
1. Calculer la température des pièces à la sortie du four.
f(0) =1375+25=1400°C.
2. Étudier le sens
de variation de la fonction f sur l’intervalle [0 ; +∞[. Ce résultat
était-il prévisible dans le contexte de l’exercice ?
f '(t) = 1375 x(-0,075) e-0,075t, négative ( le terme en exponentielle étant positif).
f(t) est décroissante.
Plongée à l'air libre, la température de la pièce chaude ne peut que diminuer..
3. Les pièces peuvent-elles être modelées 10 heures après la sortie du four ? Après 14 heures ?
f(10) = 1375 e-0,75 +25 =674,5° C, valeur supérieure à 600 °C. Pas de modelage possible.
f(14) = 1375 e-1,05 +25 =516,2° C, valeur infpérieure à 600 °C. Modelage possible.
4. On souhaite déterminer le temps minimum d’attente en heures après la sortie du four avant de pouvoir modeler les pièces.
a. Compléter l’algorithme donné pour qu’il renvoie ce temps minimum d’attente en heure (arrondi par excès à 0,1 près).

b. Déterminer ce temps minimum d’attente. On arrondira au dixième.
1375e−0,075 t+25 < 600 ; 1375e−0,075 t < 575 ; e−0,075 t < 575 /1375 ; e−0,075 t < 0,41818.
-0,075 t > ln(0,41818 ) ; t > 11,7 heures.
Sujet 22.
Les résultats seront arrondis à l’unité.
La quantité (en kg) de déchets ménagers produite par habitant d’une
ville de taille moyenne a été de 537 kg en 2019 et la municipalité
espère réduire ensuite cette production de 1,5 % par an.
Pour tout entier naturel n, on note dn la quantité (en kg) de déchets ménagers produit par habitant de cette ville durant l’année 2019 + n, on a donc d0=537.
1. Montrer par un calcul que d1=0,985×d0.
Diminution de 1,5 % = multiplication par 1-0,015 =multiplier par 0,985.
d1=0,985×d0.
2. Pour tout entier naturel n , exprimer dn+1 en fonction de dn .
dn+1 = 0,985 dn.
3. En déduire la nature de la suite (dn) puis une expression de dn en fonction de n .
Suite géométrique de raison 0,985 et de premier terme 537.
dn = 537 x 0,985n.
4. On souhaite
savoir à partir de quelle année la production moyenne de déchets
produite par chaque habitant sera inférieure à celle enregistrée en
2019 au niveau national, à savoir 513 kg. Pour cela, on considère
l’algorithme suivant rédigé en langage Python.
def année ()
n=0
d=537
while d >513
n=n+1
d = 0,985*d
return n
a. Recopier et compléter l’algorithme afin de répondre au problème posé
b. À partir de
quelle année la production moyenne de déchets produite par chaque
habitant sera-t-elle inférieure à celle enregistrée en 2019 au niveau
national ?
d1 = 528,94 ; d2 = 521 ; d3 = 513,2 ; d4 = 505,5.
A partir de 2019+4=2023, la production moyenne de déchets produite par chaque habitant
sera inférieure à celle enregistrée en 2019 au niveau national.
|
|
Exercice 3. ( 5 points).
Sujet 21.
Dans le plan muni d’un repère orthonormé, on considère les points A(4 ;−1), B(3 ;4) et C( −1 ; 1).
1. Calculer le produit scalaire suivant :
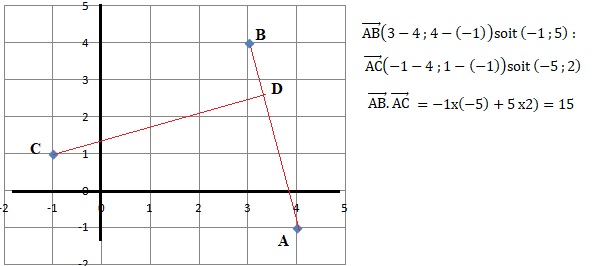
2. a. Soit D le projeté orthogonal du point C sur la droite (AB), justifier que :
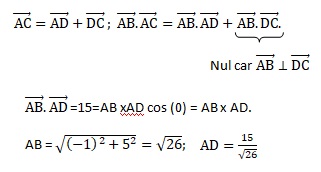
b. En déduire la longueur AD.
3. Déterminer la hauteur du triangle ABC issue de C.
AC2 =(-5)2 +22 =29 ; AD2 = 152 / 26 =225 / 26.
CD2 =AC2 - AD2 =29- 225 /26 =529 / 26 ; CD = racine carrée ( 529 / 26) = 23 /26½~4,51.
4. Calculer l’aire du triangle ABC.
AB x CD / 2 = 26½ x23 / (26½ x2) =23 / 2 = 11,5 cm2.
Sujet 22.
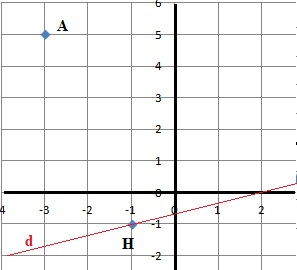
Dans un repère orthonormé on considère le point A(−3 ; 5) et la droite (d) dont une équation cartésienne est −x+3y+2=0.
1. Tracer la droite (d).
2. Déterminer les coordonnées d’un vecteur normal à la droite (d).
Un vecteur normal à la droite (d) a pour coordonnées ( -1 ; 3).
3. Déterminer une équation cartésienne de la droite perpendiculaire à (d) et passant par A.
Coordonnées du vecteur directeur de cette droite ( 1 ; -3) ; coefficient directeur de cette droite: a = -3.
Equation réduite : y = -3x+b.
A appartient à cette droite : 5 = -3 *(-3) +b ; b = -4. y = -3x-4 soit 3x +y +4=0.
4. En déduire que le point H, projeté orthogonal de A sur la droite (d), a pour coordonnées (−1;−1).
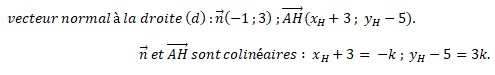
H appartient à la droite (d) : k+3 +3(3k+5)+2=0 soit 10k +20=0 ; k =-2 et xH = -1 ; yH = -1.
5. En déduire la distance entre le point A et la droite (d).
AH2 =(-1-(-3))2 +(-1-5)2 = 22+62=40 ; AH = 40½ = 2*10½.
|
|
Exercice 4. ( 5 points) Sujet 21 Une
entreprise de 1 000 employés est organisée en 3 services « A », « B »
et « C » d’effectifs respectifs 450, 230 et 320 employés. Une enquête
effectuée auprès de tous les employés sur leur temps de parcours
quotidien entre leur domicile et l’entreprise a montré que :
40 % des employés du service « A » résident à moins de 30 minutes de l’entreprise ;
20 % des employés du service « B » résident à moins de 30 minutes de l’entreprise ;
80 % des employés du service « C » résident à moins de 30 minutes de l’entreprise.
On choisit au hasard un employé de cette entreprise et on considère les événements suivants :
A : l’employé fait partie du service « A » ;
B : l’employé fait partie du service « B » ;
C : l’employé fait partie du service « C » ;
T : l’employé réside à moins de 30 minutes de l’entreprise.
1. Justifier que P(A)=0,45 puis donner PA(T)
Le service A compte 450 employés parmi les 1000 employés : P(A) = 450 / 1000 = 0,45.
PA(T)=0,40.
2. Compléter l’arbre pondéré.
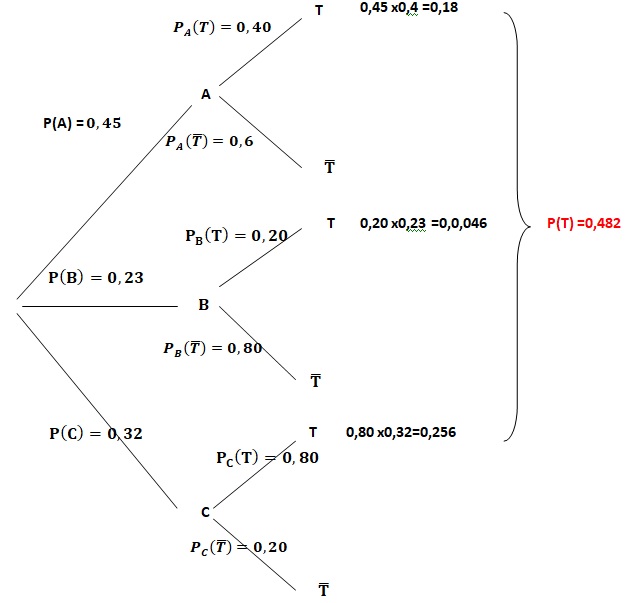
3. Déterminer la probabilité que l'employé choisi soit du service « A »
et qu’il réside à moins de 30 minutes de son lieu de travail.
P(A n T) =0,45 x 0,4 =0,18.
4. Montrer que P(T)=0,482.
P(T) = P(A n T) +P(B n T) +P(C n T) = 0,18 +0,23 x0,2 +0,32 x 0,8 =0,482.
5. Sachant qu'un employé de l’entreprise réside à moins de 30 minutes
de son lieu de travail, déterminer la probabilité qu'il fasse partie du
service C.
PT(C) =P(T n C) / P(T)=0,32 x0,8 / 0,482 =0,531.
|
Sujet 22.
Les résultats seront donnés sous forme de fractions irréductibles.
Une enquête a été menée auprès de lycéens pour estimer la proportion de
ceux qui ont déjà consommé du cannabis. Pour encourager les réponses
sincères, on met en place le protocole suivant :
Chaque adolescent lance d’abord un dé équilibré à 6 faces et
l’enquêteur qui va l’interroger ne connaît pas le résultat du lancer. À
la question « Avez vous déjà consommé du cannabis ? », l’adolescent
doit répondre :
• « non » si le résultat du lancer est 5, qu’il ait ou non déjà consommé du cannabis ;
• « oui » si le résultat du lancer est 6, qu’il ait ou non déjà consommé du cannabis ;
• « oui » ou « non » dans les autres cas, mais de façon sincère.
On note :
N : l’évènement l’adolescent a répondu « non » ;
O : l’évènement l’adolescent a répondu « oui » ;
C : l’évènement l’adolescent a déjà consommé effectivement du cannabis ;
C̅ : l’évènement l’adolescent n’a jamais consommé du cannabis.
Sur les lycéens qui ont participé à cette enquête on constate que la
probabilité qu’un adolescent ait répondu « oui » est de 0,6 , soit
p(O)=0,6.
On veut déterminer la probabilité, notée p, qu’un adolescent ait déjà consommé du cannabis.
On a donc p(C)=p .
1. Justifier que la probabilité qu’un adolescent ait répondu « oui » sachant qu’il n’a jamais consommé de cannabis est 1 / 6 .
Il a répondu "oui" en mentant, il a donc obtenu un 5. La probabilité d'obtenir 5 est égale à 1 / 6.
2. On a représenté en annexe l’arbre de probabilités représentant la situation. Compléter l’arbre.
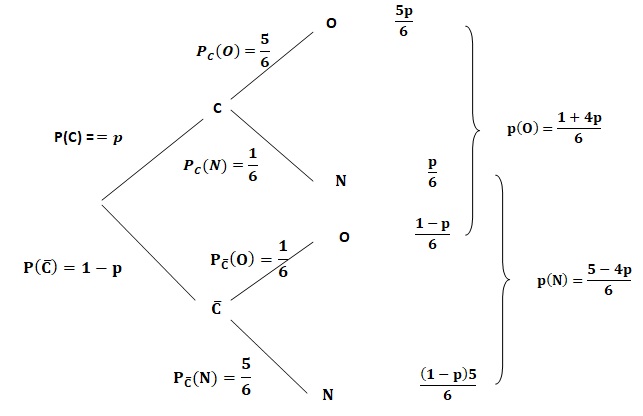
3. a. Démontrer que la probabilité p qu’un adolescent ait déjà consommé du cannabis vérifie l’équation : 2 /3 p+1 / 6=3 / 5.
(1+4p) / 6 = 0,6 = 3 / 5 ; 1 /6 +4p /6 = 3 / 5 ; 1 / 6 +2p / 3 = 3 / 5.
b. En déduire la valeur de p .
2 p / 3 = 3 /5 -1 / 6 = (18-5) / 30 = 13 / 30 ; p = 13 / 20 = 0,65.
4. Sachant qu’un
adolescent a répondu « non » pendant l’enquête, quelle est la
probabilité qu’il n’ait jamais consommé de cannabis ?
PN( non C) = P ( N n non C) / P(N) =(1-13 / 20) *5 *5/ (6 *2) =7 * 25 /(20 *12)=7 *5 / 8 =35 / 48 ~0,73.
.
|
|