Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 23
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
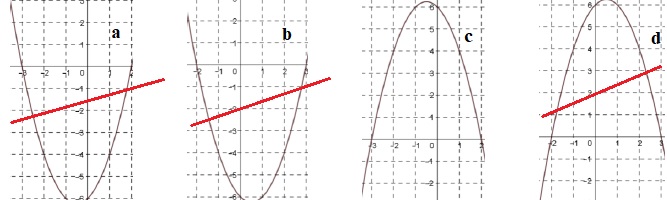
1. On considère la fonction définie sur R par f(x) = −x2 − x + 6. On admet que l’une
des quatre courbes ci-dessous représente la fonction f. Laquelle ? Réponse c.
a étant négatif, la parabole présente un maximum. L'axe de symétrie est tel que x = -b /(2a) = 1 /(-2) = -0,5.
2. On pose pour tout réel x : A(x) = e2x. On a alors, pour tout x réel :
a) A(x) = 2ex , b) A(x) = exp(x2) ; c) A(x) = ex + e2 ; d) A(x) = (ex )2. Réponse d.
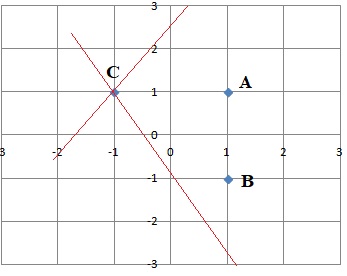
3. Le plan est muni d’un repère orthonormé.
Les droites d’équations 2x + y + 1 = 0 et 3x − 2y + 5 = 0
a) sont sécantes en A(1 ; 1). b) sont sécantes en B(1 ; −1).
c) sont sécantes en C(−1 ; 1). d) ne sont pas sécantes. Réponse c.
2xA + yA + 1 = 0 donne 2+1+1 =0, faux. A n'appartient pas à cette droite.
3xA -2 yA + 5 = 0 donne 3-2+5 =0, faux. A n'appartient pas à cette droite.
2xB + yB + 1 = 0 donne 2-1+1 =0, faux. B n'appartient pas à cette droite.
3xB -2 yB + 5 = 0 donne 3+2+5 =0, faux. B n'appartient pas à cette droite.
2xC + yC + 1 = 0 donne -2+1+1 =0, vrai. C appartient à cette droite.
3xC -2 yC + 5 = 0 donne -3-2+5 =0, vrai. C appartient à cette droite..
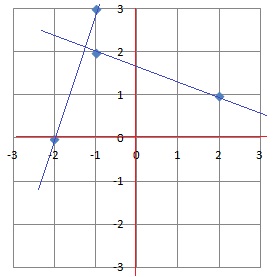
4. Le plan est muni d’un repère orthonormé.
Les droites d’équations x + 3y − 5 = 0 et 3x − y + 6 = 0 sont :
a) perpendiculaires. b) sécantes non perpendiculaires. c) parallèles. d) confondues. Réponse a.
Coordonnées d'un vecteur normal à la première droite (1 ; -3).
Coordonnées d'un vecteur normal à la seconde droite (3 ; -1).
5. On considère la fonction Python ci-dessous :.
def suite(n)
u=2
k=0
while k < n
u = u+k
k=k+1
return u
Quelle valeur renvoie l’appel suite(5) ?
a) 5 ; b) 8 ; c) 12 ; d) 17. Réponse c.
u
|
2
|
2
|
3
|
5
|
8
|
12
|
k
|
0
|
1
|
2
|
3
|
4
|
5
|
k < 5 ?
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
faux
|
Sujet 24.
1. Dans un repère orthonormé, un vecteur normal à la droite d’équation 4x + 5y − 32 = 0 est le vecteur :

Réponse c.
2. Dans un repère orthonormé, le projeté orthogonal du point A(7 ; 9) sur la droite d’équation 4x + 5y − 32 = 0 est le point :
a) H(7 ; 0,8) ; b) H(3 ; 4) ; c) H(4 ; 3,2) ; d) H(4 ; 5). Réponse b.
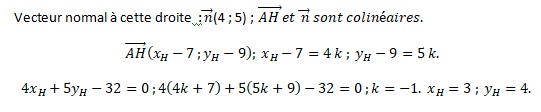
3. Dans un repère orthonormé, une équation du cercle de centre A(−1 ; 3) et de rayon 2 est :
a) x2 − 1 + y2 = 22; b) x2 + 2x + 1 + y2 − 6y + 9 = 2
c) (x + 1)2 + (y − 3)2 = 22 ; d) (x − 1)2 + (y + 3)2 = 22. Réponse c.
4. Dans un repère orthonormé, la parabole d’équation y = 3x2 − 9x + 5 a pour sommet le point S et pour axe de symétrie la droite Δ. Les coordonnées de S et l’équation de Δ sont :
a) S(1,5 ; -7 /4) et D : x=1,5 ; b) S(1,5 ; -7 /4) et D : y=-7 /4 ;
c) S(3 ; 5) et D : x=3 ;d) S(3 ; 5) et D : y=5.
Axe de symétrie x = -b /(2a) =9 / 6= 1,5.
Sommet 1,5 et f(1,5) =3 *2,25 -9*1,5 +5 =-1,75 = -7 /4. Réponse a.
5. On considère l’inéquation −3x2 + 9x − 5 > 0. L’ensemble S des solutions de cette inéquation est (x1 et x2 sont deux réels tels que x1 < x2 pour les propositions b) et d)) :
a) aucune ; b) de la forme ] − ∞ ; x1 [ ∪ ] x2 ; +∞ [
c) ℝ ; d) de la forme ] x 1 ; x2 [.
La parabole présente un maximum ( a < 0). Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 23. On considère la fonction f définie sur [0; +∞[ par f(x) =ex /(1+x).
On note Cf la représentation graphique de f dans un repère du plan.
1. Déterminer les coordonnées du point A, point d’intersection de la courbe Cf avec l’axe des ordonnées.
x = 0 ; f(0) =1 ; A (1 ; 0).
2. La courbe Cf coupe-t-elle l’axe des abscisses ? Justifier la réponse.
ex est toujours positif ; 1+x est positif ; ex > 1+x ; f(x) > 1. La courbe ne coupe pas l'axe des abscisses.
3. On note f ′ la dérivée de la fonction f sur [0; +∞[. Montrer que, pour tout réel x de l’intervalle [0; +∞[, f '(x) =x ex /(1+x)2.
On pose u = ex et v = x+1 ; u' = ex ; v' = 1 ; (u'v-v'u) / v2 =[(x+1)ex-ex) / (1+x)2 =x ex /(1+x)2.
4. Étudier le signe de f '(x) sur [0; +∞[. En déduire le sens de variation de f sur [0; +∞[.
ex est positif ; un carré est toujours positif ; x est positif.
f '(x) est positive et f(x) est strictement croissante sur [0; +∞[.
5. On note T la tangente à Cf au point A d’abscisse 1,6. La tangente T passe-t-elle par l’origine du repère ? Justifier la réponse.
Coefficient directeur de T = f '(1,6) =1,6 e1,6 /2,62 ~1,172.
f(1,6) =e1,6 / 2,6 ~1,905.
Equation de la tangente T : y = 1,6 e1,6 /2,62 x +b.
T passe par le point de coordonnées (1,6 ; e1,6 / 2,6) : e1,6 / 2,6 =1,62 e1,6 /2,62 +b ;
b =e1,6 / 2,6(1 -1,62 / 2,6) ~0,03, différent de zéro.
T ne passe pas par l'origine du repère.
Sujet 24.
On considère une fonction f définie et dérivable sur l’intervalle [−4 ; 2]. La fonction dérivée de f est notée f ′.
Dans le repère orthonormé ci-dessous, la courbe C est la courbe représentative de f sur l’intervalle [−4 ; 2].
Le point A est le point de la courbe C d’abscisse −1. La droite T est la tangente à la courbe C en A.
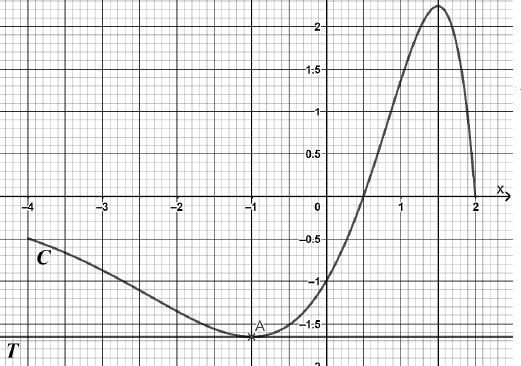
1. Par lecture graphique, donner la valeur de f ′(−1).
La tangente T étant horizontale, f '(-1) = 0.
2. Résoudre, graphiquement, l’inéquation f ′(𝑥) ≤ 0.
f '(x) négative ou nulle ; f(x) décroissante ou présente un extrémum :
[-4 ; -1] union [1,5 ; +2].
On admet que la fonction f est définie sur [−4 ; 2] par f(x)= (−x2 + 2,5x − 1)ex.
3. Vérifier que, pour tout réel x de l’intervalle [−4 ; 2], f '(x) = (−x2 + 0,5x + 1,5)ex .
On pose u = −x2 + 2,5x − 1 et v = ex ; u' = -2x+2,5 ; v' = ex ; u'v +v'u = (-2 x+2,5)ex +ex(−x2 + 2,5x − 1)=(−x2 + 0,5x + 1,5)ex .
4. Étudier le signe de la fonction f ′ sur l’intervalle [−4 ; 2].
5. En déduire les variations de f sur l’intervalle [−4 ; 2].
ex est positif ; solutions de −x2 + 0,5x + 1,5=0 ; discriminant : 0,52 -4*(-1)*1,5 =6,25 =2,52.
Solutions : (-0,5 ±2,5) / (-2) soit 1,5 et -1.
Le coefficient a étant négatif, la parabole présente un maximum et f
'(x) > 0 sur ]-1 ; 1,5[, fonction strictement croissante.
f '(x) < 0 sur [-4 ; -1[ union ]1,5 ; 2], f(x) strictement décroissante.
f '(-1) = f '(1,5) =0 : f(x) présente un minimum en x = -1 et un maximum en x = 1,5.
|
|
Exercice 3. ( 5 points).
Sujet 23.
Une entreprise a fabriqué en un mois 1500 chaudières, dont 900 chaudières à cheminée et 600 chaudières à ventouse.
On a constaté, dans ce lot, que :
1 % des chaudières à cheminées ont un défaut
6 % des chaudières à ventouses ont un défaut.
On prélève au hasard le numéro de série d’une chaudière de la production de ce mois.
On considère les évènements suivants :
C : « Le numéro de série est celui d’une chaudière à cheminée »
V : « Le numéro de série est celui d’une chaudière à ventouse »
D : « Le numéro de série est celui d’une chaudière défectueuse »
1. Recopier et compléter sur la copie le tableau à double entrée suivant :
|
nombre chaudières à cheminée
|
nombre chaudières à ventouse
|
total
|
nombre chaudières défectueuses
|
9
|
36
|
45
|
| nombre chaudières non défectueuses |
891
|
564
|
1455
|
total
|
900
|
600
|
1500
|
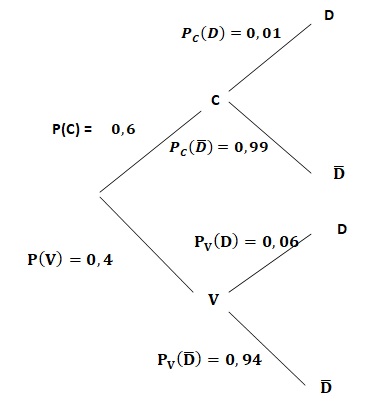
2. Recopier et compléter l’arbre pondéré suivant
:
3. Calculer la probabilité que le numéro de série soit celui d’une chaudière défectueuse.
P(D)=45 / 1500 =0,03
4. Déterminer PD(V). Interpréter le résultat dans le contexte de l’exercice.
PD(V)= P( V n D) / P(D) =36 /45 =0,8.
La probabilité qu'une chaudière soit à ventouse, sachant qu'elle est défectueuse, est égale à 0,8.
5. Les évènements D et V sont-ils indépendants ?
P(D) =45 / 1500 =0,03 ; P(V) =600 /1500 = 0,4 ; P(D n V) =36 / 1500 =0,024.
P(D n V) = P(D) x P(V), les événements sont indépendants.
Sujet 24.
Laura
reçoit chaque jour beaucoup de courriels. Pour se protéger des
courriels indésirables, elle achète un logiciel anti-spam. Chaque jour,
35 % des courriels reçus par Laura sont
indésirables ; 95 % des courriels indésirables sont automatiquement
bloqués par le logiciel anti-spam. Parmi les courriels qui ne sont pas
indésirables, le logiciel anti-spam en bloque
2 %.
On choisit au hasard un courriel reçu par Laura. Chaque courriel a la
même probabilité d’être choisi. On considère les événements suivants :
- I : « le courriel choisi est indésirable »,
- S : « le logiciel anti-spam bloque le courriel choisi ».
1. Compléter l’arbre de probabilité traduisant la situation.
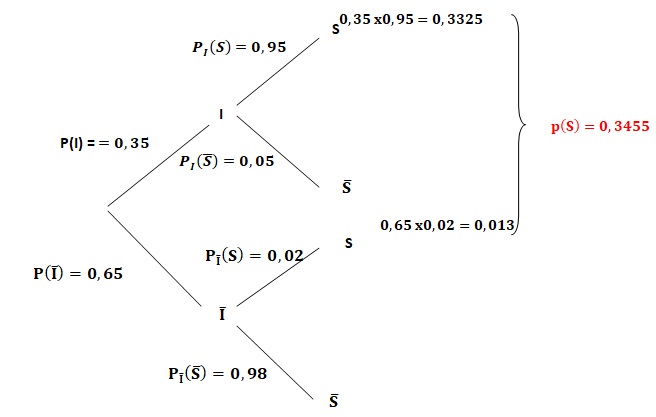
2. Calculer la probabilité que le courriel reçu par Laura ne soit pas indésirable et soit bloqué par le logiciel anti-spam.
P(non I n S) =0,65 x0,02 =0,013.
3. Montrer que P(𝑆) = 0,3455.
4. Le logiciel anti-spam a bloqué un courriel reçu par Laura. Calculer la probabilité que ce courriel soit indésirable.
PS(I) =P(S n I) / P(S) = 0,3325 / 0,3455 =0,962.
5. Le fournisseur
du logiciel anti-spam affirme que son logiciel se trompe dans moins de
2 % des cas. Est-ce vrai ? Justifier votre réponse.
P(I n non S) + P (non I n S )=0,35 x0,05 +0,65 x0,02 =0,0305 ( 3,05 % supérieur à 2 %). C'est faux.
|
|
Exercice 4. ( 5 points) Sujet 23 Un
jeu vidéo fait évoluer un personnage sur un parcours semé d’obstacles.
Au début du parcours, ce personnage est doté de 1 000 pions noirs dans
son sac et il n’a pas de pion blanc.
Le nombre de pions noirs diminue au cours du jeu.
Le personnage gagne 10 pions blancs par minute jouée.
Chaque partie est chronométrée et dure 45 minutes. Au bout des 45
minutes, la partie s’arrête et le joueur a gagné si le nombre de pions
blancs gagnés est supérieur ou égal au nombre de pions noirs du sac.
1. Etude de l’évolution du nombre de pions blun enancs
On note un le nombre de pions blancs obtenus au bout de n minutes de jeu.
Ainsi u0=0.
Déterminer la nature de la suite (un) et en déduire, pour tout entier n, l’expression de un fonction de n.
un = 10n, suite arithmétique de raison r = 10 et de premier terme zéro.
2. Etude de l’évolution du nombre de pions noirs.
Lucas estime qu’au cours d’une partie, le nombre de ses pions noirs
diminue de 2 % par minute. Il voudrait savoir si cette évolution est
suffisante pour gagner, ou s’il doit poursuivre son entrainement.
On note vn le nombre de pions noirs restant à la n-ième minute.
Ainsi v0=1000.
a. Justifier que v1=980.
Diminue de 2 % signifie multiplier par 1-2 /100 = 0,98.
v1 = 0,98 v0.
b. Déterminer la nature de la suite (vn) et en déduire, pour tout entier n, l’expression de v en fonction de n.
Suite géométrique de raison 0,98 et de premier terme 1000.
vn = 1000 *0,98n.
3. On a calculé les premiers termes des suites (un) et (vn) à l’aide d’un tableur. La feuille de calcul est donnée ci-dessous.
Lucas peut-il gagner la partie ?
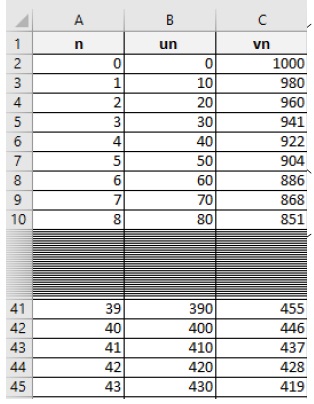
Lucas peut gagner si un > vn avec n < 45.
u43 = 430 ; v43 =419 ; Lucas peut gagner.
|
Sujet 24.
Durant
le mois de janvier 2020, une entreprise produit 2 500 flacons de parfum
ce qui correspond exactement au nombre de flacons commandés. Le
propriétaire de l’entreprise
décide d’augmenter chaque mois la production de 108 flacons et il
espère que le nombre de flacons commandés augmentera chaque mois de 3,8
%.
On considère la suite (fn ) où pour tout entier naturel n, fn modélise le nombre de flacons produits lors du mois de rang n après janvier 2020 ; ainsi f0 est le nombre de flacons
produits en janvier 2020, f1 le nombre de flacons produits en février 2020, etc.
De la même manière, on considère la suite (cn) où pour tout entier naturel n, cn modélise le nombre potentiel de flacons commandés lors du mois de rang n après janvier 2020. On a
donc f0 = c0 = 2 500.
1. Déterminer, en
expliquant les calculs effectués, le nombre de flacons produits et le
nombre potentiel de flacons commandés en février 2020.
f1 = 2500 +108 =2608 ; c1 =2500 x1,038 =2595.
2. Déterminer la nature des suites (fn) et (cn).
(fn) ; suite arithmétique de raison r = 108 et (cn) suite géométrique de raison 1,038.
3. Exprimer, pour tout entier n, fn et cn en fonction de n.
cn = 2500 x 1,038n ; fn = 2500 +108n.
4. On admet que,
selon ce modèle, au bout d’un certain nombre de mois le nombre
potentiel de flacons commandés dépassera le nombre de flacons produits.
Reproduire et compléter sur la copie l’algorithme, écrit en Python,
afin qu’après son exécution la variable n contienne le nombre de mois à
attendre après le mois de janvier 2020 pour que le nombre
potentiel de flacons commandés dépasse le nombre de flacons produits.
n =0
f = 2500
while c < f
n=n+1
f =f+ f+108
c =c+c *1,038
5. De début janvier
2020 à fin décembre 2020, la production globale dépassera-t-elle le
nombre de commandes potentielles ? Expliquer votre démarche.
Somme des 12 premiers termes de la suite arithmétique de premier terme 2500 et de douxième terme 2500 +11 x108=3688
Nombre de flacons produits : 12(2500 +3688) / 2 = 37 128.
Somme des 12 premiers termes de la suite géométrique de premier terme 2500 et de raison 1,038.
Nombre de flacons commandés : 2500(1-1,03812) /(1-1,038)= 37 136.
La production reste inférieure aux commandes potentielles.
.
|
|