Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 25
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Dans le plan muni d’un repère orthonormé, l’ensemble des points M de coordonnées (𝑥, 𝑦)
vérifiant : (x + 1)2 + (y − 1)2 = 9 est :
a) un cercle ; b) une droite ; c) une parabole ; d) l’ensemble vide.
Cercle de centre (-1 ; 1) et de rayon 3.
2. Combien y-a-t-il de fonctions polynômes du second degré qui s’annulent en 1 et en 3 ?
a) 0 ; b) 1 seule ; c) 2 ; d) une infinité.
P(x)=(x-1)(x-3)=x2-4x+3.
3. Une fonction polynôme du second degré :
a) est nécessairement de signe constant sur R
b) n’est jamais de signe constant sur R
c) est nécessairement positive sur R
d) peut être ou non de signe constant sur R. Réponse d.
Elle est de signe constant si le discriminant est négatif ( la courbe ne coupe pas l'axe des abscisses).
4. Pour tout réel x, e2x+1 =
a) e2x + e ; b) e2x × e vrai ; c) (ex+1)2 ; d) (2x + 1) × e.
5. Dans un repère orthonormé, la droite d d’équation cartésienne 2x − 5y − 4 = 0
a) coupe l’axe des ordonnées au point de coordonnées (0 ; −4).
Faux, 2 *0 -5*(-4)-4 =-2, diffère de zéro.
b) passe par le point de coordonnées (2 ; 0,2).
Faux : 2*2-5*0,2-4 =-1 diffère de zéro.
c) admet pour vecteur normal le vecteur de coordonnées (2 ; -5). Vrai.
d) admet pour vecteur directeur le vecteur de coordonnées (2 ; -5).
Sujet 26.
1. Pour tout réel x, e2x / ex+1 est égale à :
a) ex−1 ; b) e3x+1 ; c) 2x/(x+1) ; d) e.
e2x-(x+1) =ex-1. Réponse b.
2. Dans le plan muni d’un repère, les courbes représentatives des fonctions
f(x)=15x2+10x−1 et g(x)=19x2−22x+10 ont :
a) aucun point d’intersection
b) un seul point d’intersection
c) deux points d’intersection
d) quatre points d’intersection.
15x2+10x−1=19x2−22x+10 ; 4x2-32x +11 = 0 ; discriminant : (-32)2 -4*4*11=848.
Le discriminant étant positif, les courbes ont deux points d'intersection.
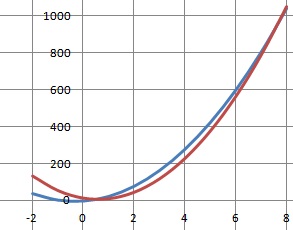
Réponse c.
3.
Le plan est rapporté à un repère orthonormé. Le cercle de centre A de
coordonnées ( 3 ; - 1) et de rayon 5 a pour équation cartésienne :
a) ( x + 3)2 + ( y- 1)2 = 25
b) ( x− 3)2 + ( y+1)2 = 5
c) ( x + 3)2 + ( y- 1)2 = 5
d) ( x− 3)2 + ( y+1)2 = 25. Réponse d.
4. Dans un repère orthonormé, la droite d d’équation cartésienne 3 x + 2 y + 4 = 0 admet un vecteur normal de coordonnées :
a) (2−3) ; b) (−3 ; 2) ; c) (3 ; 2) ; d) (2 ; 3). Réponse c.
5. Le plus petit entier naturel n tel que la somme 1+2+3+4+⋯+n soit supérieure à 5000 est égal à :
a) 1000 ; b) 500 ; c) 200 ; d) 100
Somme des n premiers termes d'une progression arithmétique de raison 1 et de premier terme 1 :
si n=100 : 100(1+100 ) / 2 =5050 ; n(1+n) / 2 > 5000 ; n2+n >10000 ; n2+n -10000 > 0.
n2+n -10000 =0 ; discriminant : 1+40000 = 40001 ~2002; solution retenue (-1+200) / 2 ~100. Réponse a.
|
|
Exercice 2. ( 5
points) Sujet 25. Le
principe d’un Escape Game est le suivant : une équipe de participants
est enfermée à l’intérieur d’une salle à thème et doit réussir à en
sortir en moins d’une heure (on parle alors
de partie réussie). Au-delà d’une heure, les participants sont libérés et la partie est perdue.
Un exploitant d’Escape Game propose à ses participants de faire deux
parties à la suite : la première partie se déroule dans la salle à
thème « Espion », la seconde partie dans la salle à thème « Musée ». Il
dispose des données suivantes :
lorsqu’une équipe joue dans la salle à thème « Espion », la
probabilité qu’elle réussisse sa partie « Espion » est égale à 0,5 ;
lorsqu’une équipe a réussi la partie « Espion», la probabilité qu’elle réussisse sa partie « Musée » est égale à 0,6 ;
lorsqu’une équipe n’a pas réussi la partie « Espion », la probabilité qu’elle réussisse sa partie « Musée » est égale à 0,45.
Une équipe est choisie au hasard. On note les événements suivants :
E : « l’équipe réussit la partie « Espion » ;
M : « l’équipe réussit la partie « Musée ».
1. Recopier et compléter l’arbre de probabilités suivant :
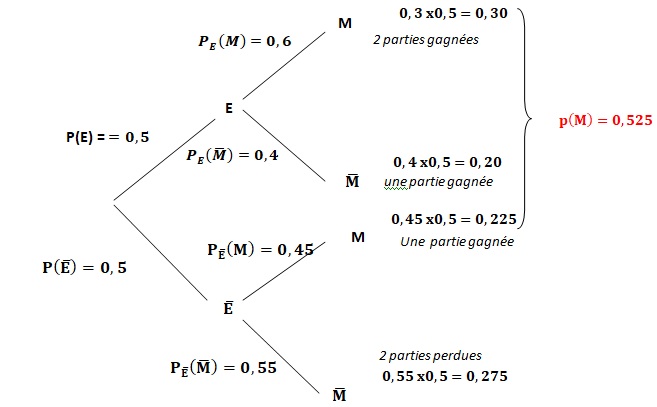
2. Déterminer la probabilité que l’équipe réussisse les deux parties.
P(E n M)=0,5 x0,6 = 0,30.
3. Montrer que la probabilité que l’équipe réussisse la partie « Musée » est égale à 0,525.
P(E n M) + P(non E n M) =0,30 +0,5 x0,45 =0,525.
4. Quelle est la
probabilité qu’une équipe échoue à la partie « Espion » sachant qu’elle
a réussi la partie « Musée » ? On donnera la réponse arrondie à 10−2.
PM (E) = P (E n M) / P(M) =0,3 / 0,525 ~0,57.
5. Pour chacune des
deux parties qui sont gagnées, une équipe reçoit 2 € de réduction pour
une prochaine visite. Elle peut donc recevoir 0, 2 ou 4 € de réduction.
Si un très grand nombre d’équipes jouent les deux parties, quel est le
montant moyen de la réduction obtenue à la fin des deux parties ?
Expliquer la démarche.
On définit une variable aléatoire X ayant pour valeur la réduction obtenue.
xi
|
0
|
2
|
4
|
P(X=xi)
|
0,275
|
0,20 +0,225 = 0,425
|
0,30
|
Réduction moyenne : 2 x0,425 +4 x0,30 =2,05 €.
Sujet 26.
On considère la fonction dérivable f définie sur R par f(x)=8x3−6x2−2.
On note f ′ la fonction dérivée de la fonction f. Soit C la courbe
représentative de f dans un plan muni d’un repère orthogonal.
1. a. Justifier que pour tout réel x, f(x) = ( x- 1 ) ( 8x2+ 2x +2 ).
On développe ( x- 1 ) ( 8x2+ 2x +2 ) =8x3+2x2+2x-8x2-2x-2=f(x)
b. En déduire que la courbe C coupe l’axe des abscisses en un seul point A dont on donnera les coordonnées.
Solution de ( x- 1 ) ( 8x2+ 2x +2 ) =0 :
x-1 =0 soit x = 1.
8x2+ 2x +2 =0 ; discriminant : 22-4*2*8 = -60. Le discriminant étant négatif, 8x2+ 2x +2 =0ne possède pas de solution réelle.
Ordonnée de A : f(1) =8-6-2=0 ; A(1 ; 0).
2. a. Justifier que pour tout réel x, f '(x) =12x(2x−1).
f '(x) = 24x2-12x = 12x(2x-1)
b. En déduire le tableau de variations de la fonction f.
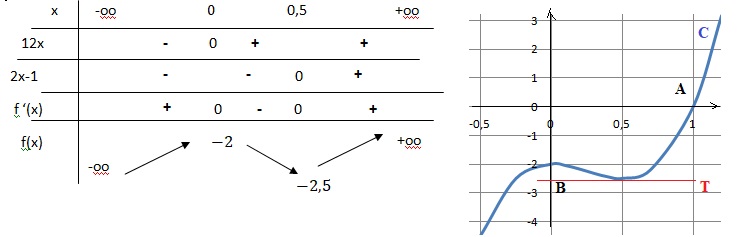
3. Le point B de coordonnées (0 ;-2,5 ) appartient-il à la tangente T à la courbe C au point B d’abscisse x =0,5 ? Justifier.
Coefficient directeur de T : f '(0,5) =0.
Equation de la tangente : y = b = f(0,5) = -2,5.
B appartient à la tangente.
|
|
Exercice 3. ( 5 points).
Sujet 25.
En
France métropolitaine, 2018 a été l'année la plus chaude d’après les
relevés météorologiques. La température moyenne y a été de 14 °C; elle
a dépassé de 1,4 °C la normale de référence calculée sur la période
1981-2010. (Source : site Météo France)
1. Pour modéliser
la situation, on considère l’année 2018 comme l’année zéro et on
suppose que cette hausse moyenne de 1,4°C par an se poursuit chaque
année. Pour tout entier naturel n, on note alors Tn la température moyenne annuelle en France pour l’année 2018+n.
a. Quelle est la nature de la suite (Tn) ainsi définie ? On donnera son premier terme et sa raison.
Suite arithmétique de raison r = 1,4 et de premier terme T0 =14.
b. On considère
qu’au-delà d’une température moyenne de 35°C les corps ne se
refroidissent pas et il devient insupportable pour les humains de
continuer à habiter cette région que l’on qualifie alors d’inhabitable.
Selon le modèle considéré, en quelle année la France deviendrait-elle
inhabitable pour les humains ? Justifier.
Tn =14 +1,4 n = 35 ; 1,4 n = 35-14=21 ; n = 21 / 1,4 =15 (année 2018+15 =2033).
2. À cause du
réchauffement climatique, certaines régions risquent de connaître une
baisse de 10 % par an des précipitations moyennes annuelles mesurées en
millimètres (mm). Dans une région du nord de la France, les
précipitations moyennes annuelles étaient de 673 mm en 2018. On
considère l’année 2018 comme l’année zéro et on suppose que cette
baisse de 10 % par an se poursuit chaque année. Pour tout entier
naturel n, on note Pn les précipitations annuelles moyennes en mm dans cette région pour l’année 2018+n.
a. Quelle est la nature de la suite (Pn) ainsi définie ? On donnera son premier terme et sa raison.
Suite géométrique de raison 1-10 /100 = 0,9 et de premier terme P0 =673.
b. Pour tout entier naturel n, exprimer Pn en fonction de n.
Pn = P0x0,9n.
c. On donne le programme Python suivant :
def precipitations(J):
I=673
n=0
while I > J:
I = 0.9*I
n = n+1
return n+2018
L’exécution de « precipitations(300) » renvoie la valeur 2026 . Que représente cette valeur pour le problème posé ?
A partir de 2026, les précipitations moyennes dans cette région seront inférieures à 300 mm.
Sujet 26.
Un
parfumeur propose l’un de ses parfums, appelé « Fleur Rose », et cela
uniquement avec deux contenances de flacons : un de 30 ml ou un de 50
ml. Pour l'achat d'un flacon « Fleur Rose », il propose une offre
promotionnelle sur un autre parfum appelé « Bois d’ébène ». On dispose
des données suivantes :
58 % des clients achètent un flacon de parfum « Fleur Rose » de 30 ml
et, parmi ceux-là, 24 % achètent également un flacon du parfum « Bois
d’ébène » ;
42 % des clients achètent un flacon de parfum « Fleur Rose » de 50 ml
et, parmi ceux-là, 13 % achètent également un flacon du parfum « Bois
d’ébène ».
On admet qu’un client donné n’achète qu’un seul flacon de parfum «
Fleur de Rose » (soit en 30 ml soit en 50 ml), et que s’il achète un
flacon du parfum « Bois d’ébène », il n’en achète aussi qu’un seul
flacon.
On choisit au hasard un client achetant un flacon du parfum « Fleur Rose ». On considère les événements suivants :
F : « le client a acheté un flacon « Fleur Rose » de 30 ml » ;
B : « le client a acheté un flacon « Bois d’ébène ».
1. Construire un arbre pondéré traduisant les données de l’exercice.
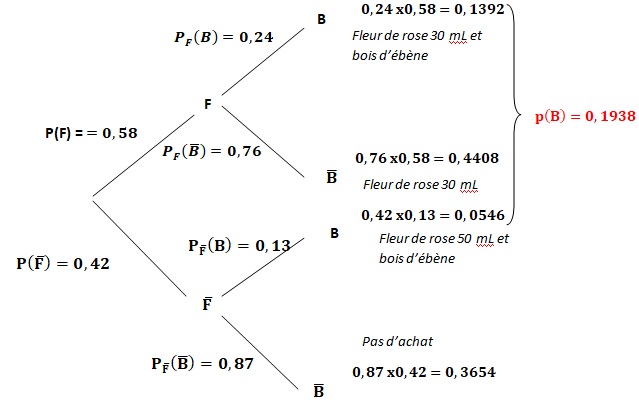
2. Calculer la probabilité P(F∩B).
P(F∩B)=0,58 x0,24 =0,1392.
3. Calculer la probabilité que le client ait acheté un flacon « Bois d’ébène ».
P(F∩B) + P(non F∩B)=0,1392 +0,42 x0,13 =0,1938
4. Un
flacon « Fleur Rose » de 30 ml est vendu 40 €, un flacon « Fleur Rose »
de 50 ml est vendu 60 € et un flacon « Bois d’ébène » 25 €. On note X
la variable aléatoire correspondant au montant total des achats par un
client du parfum « Fleur Rose ».
a. Déterminer la loi de probabilité de X.
xi
|
0
|
40
|
65
|
85
|
P(X=xi)
|
0,3654
|
0,4408
|
0,1392
|
0,0546
|
b. Calculer l’espérance de X et interpréter le résultat dans le contexte de l’exercice.
E(X) =40 x0,4408 +65 x0,1392 +85 x0,0546 =17,632 +9,048 +4,641 =31,32 € ( prix moyen d'un achat).
|
|
Exercice 4. ( 5 points) Sujet 25 Soit f la fonction définie sur [0;+∞[ par f(x)=−x2+2x+4. Dans le plan muni d’un repère orthonormé, on note C sa courbe représentative.
1. Déterminer les variations de la fonction f sur [0;+∞[ .
f '(x) = -2x+2.
Si x > 1, f '(x) est négative et f(x) est strictement décroissante.
Si x appartient à [0 ; 1[, f '(x) est positive et f(x) est strictement croissante.
Pour x = 1, f '(x) =0, f(x) présente un maximum.
2. Déterminer la
valeur exacte de l’abscisse du point A, intersection de la courbe C et
de l’axe des abscisses, puis en donner une valeur approchée à 10−2 près.
−x2+2x+4=0 ; discriminant : 22-4*(-1)*4 =20 =( 2*5½)2.
Solution retenue : (-2-2*5½) / (-2)=1+5½~3,23.
3. On note T la tangente à la courbe C au point B d’abscisse 2.
Déterminer l’équation réduite de la droite T.
Coefficient directeur : f '(2) = -2*2+2 = -2.
y = -2x +b ;
B (2 ; f(2) =4) appartient à T : 4 = -2*2+b ; b = 8.
y = -2x+8.
4. Tracer la droite T sur le graphique fourni.
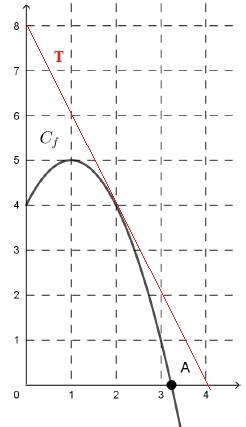
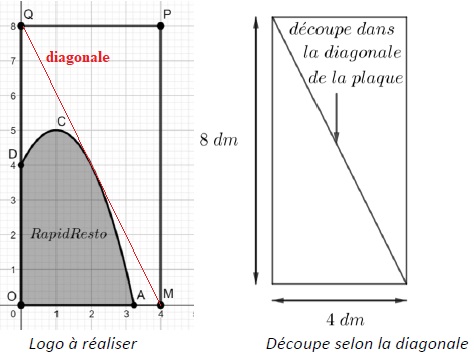
5. On admet que la courbe C est toujours en-dessous de la droite T.
La société Logo reçoit une commande de l’entreprise RapidResto, qui lui
demande de confectionner des logos dans des plaques rectangulaires de
largeur 4 dm et de hauteur 8 dm selon le modèle ci-dessous. Le bord
supérieur du logo est modélisé par la courbe C tracée dans le repère
orthonormé dont l’unité graphique est le décimètre (dm). Les figures
ci-dessous ne sont pas à l’échelle.
Dans un souci d’économie, l’entreprise Logo espère pouvoir réaliser
deux logos identiques dans une seule plaque, en la coupant dans sa
diagonale. Est-ce possible ? Justifier à l’aide des questions
précédentes.
Cela est possible, la courbe C étant en dessous de T.
|
Sujet 26.
D’après
l’ADEME (Agence De l’Environnement et de la Maîtrise de l’Énergie),
chaque français a produit une masse moyenne de 365 kg de déchets
ménagers en 2018.
Un maire, étant informé que la masse moyenne de déchets ménagers dans
sa commune en 2018 était de 400 kg par habitant, décide d’une campagne
annuelle de sensibilisation au recyclage qui conduit à une réduction de
cette production de 1,5 % par an, et cela dès l’année 2019.
On modélise alors la masse moyenne de déchets ménagers par habitant calculée en fin d’année dans cette commune par une suite (dn) où pour tout entier naturel n, dn correspond à la masse moyenne de déchets ménagers par habitant, en kg, pour l’année 2018+ n. Ainsi, d0=400.
1. Prouver que d1=394. Interpréter ce résultat.
d1 = 400 (1-1,5 /100) = 400 x0,985 =394.
2. a. Déterminer la nature de la suite (dn). Préciser sa raison et son premier terme.
Suite géométrique de raison 0,985 et de premier terme 400.
b. Pour tout entier naturel n, exprimer dn en fonction de n.
dn = 400 x0,985n.
3. a. D’après le
tableau de valeurs suivant, en quelle année la masse moyenne de déchets
ménagers par habitant deviendra-t-elle inférieure à 365 kg ?
n
|
4
|
5
|
6
|
7
|
8
|
dn
|
376,53
|
370,89
|
365,32
|
359,84
|
354,45
|
n = 7, année 2019+7 = 2026.
b. Écrire une
fonction Python qui retourne l’année à laquelle la masse moyenne de
déchets ménagers par habitant de la commune devient inférieure à 365 kg.
def masse(J):
I=400
n=0
while I > 365 :
I = 0.985*I
n = n+1
return n+2019
|
|