Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 39
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1.Pour tout réel x, cos(25p + x) est égal à :
a) cos(x) ; b) - cos( x) ; c) cos(- x) ; d) -1. Réponse b.
25p= 12*(2p) +p ; cos(25p + x) = cos(p + x) = - cos(x).
2. On considère une fonction f définie et dérivable sur l’intervalle [−10 ; 10].
On donne ci-dessous le tableau de variation de la fonction f :
 On note c la courbe représentative de f dans le plan muni d’un repère.
On note c la courbe représentative de f dans le plan muni d’un repère.
La tangente à la courbe c au point d’abscisse 3 a pour coefficient directeur :
a) 0 ; b) 3; c) 4 ; d) 10. Réponse a.
f '(3) =0, la tangente à la courbe est horizontale, son coefficient directeur est nul.
3. E et F sont deux événements indépendants d’un même univers.
On sait que p(E) = 0,4 et p(F) = 0,3 alors :
a) p(E ∪ F) = 0,7 ; b) p(E ∩ F) = 1,2 ; c) p(E ∩ F) = 0 ; d) p(E ∩ F) = 0,12.
E et F sont deux événements indépendants : p(E ∩ F) = p5E) * p(F) = 0,4 *0,3 = 0,12. Réponse d.
4. L’ensemble des solutions de l’inéquation −3x2 + 11x + 1 ≤ −3 est :
a) {−1 /3 ; 4} ; b) [−1 /3 ; 4] ; c) ]− ∞ ; −1 / 3] ∪ [4 ; +∞[ ; d) ]− ∞ ; 1 /3[ ∪ ]4 ; +∞[.
Solutions de −3x2 + 11x + 1+3=0 ; discriminant : D =112-4*4*(-3)=169 = 132.
x1 = (-11 +13) / (-6) = -1 / 3 et x2 = (-11-13) / (-6) =4.
a étant négatif, la parabole présente une maximum.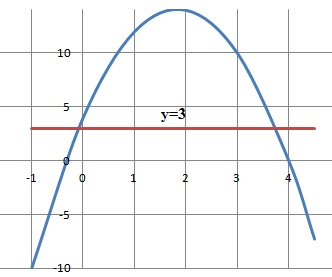
Réponse c.
5. La loi de probabilité d’une variable aléatoire X est donnée par ce tableau :
xi
|
-3
|
2
|
5
|
10
|
p(X=xi)
|
0,3
|
0,21
|
0,13
|
0,36
|
On peut en déduire que :
a) p(X > 2) = 0,49 ; b) p(X > 2) = 0,51 ; c) p(X ≥ 2) = 0,49 ; d) p(X ≥ 2) = 0,51.
p(X >2) =0,13 +0,36 = 0,49 ; p(X >2) =0,21 +0,13 +0,36 = 0,70 ;
Réponse a.
Sujet 40.
1. Pour tout réel x, sin(7p − x) est égal à :
a) sin x ; b) − sin x ; c) cos x ; d) − cos x.
sin(6p +p- x)=sin (p-x) = sin x. Réponse a.
2. Dans laquelle des quatre situations proposées ci-dessous le produit scalaire est-il 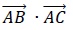 égal à 6 ? égal à 6 ?
a) ABC est un triangle tel que : AB = 6, AC = 4 et BC = 8.
b) Dans un repère orthonormé du plan :
A(−3; 5), B(2; −2) et C(1; 7). Vrai.
Coordonnées du vecteur AB ( 2-(-3) ; -2-5) soit (5 ; -7).
Coordonnées du vecteur AC (1-(-3) ; 7-5) soit (4 ; 2).
Produit scalaire de ces deux vecteurs : 5 x4 +(-7) x2 ) = 20-14=6.
c) ABC est un triangle rectangle en B tel que : AB = 3 et AC= 2 .
d) ABC est un triangle tel que :AB = 6, AC = 4 et l'angle (BAC) = 30° Faux.
AB x AC x cos 30 = 6 x4 x0,866 ~20,78.
3. On considère la fonction f définie sur R par : f(x) =(3x+4) /(x2+1).
f est dérivable sur R et, pour tout réel x, f ′(x) est égal à :
a) 3 / (2x) ; b) (9x2+8x+3) / (x2+1)2 ; c ) (-3x2-8x+3) / (x2+1)2 ; d) 9x2+8x+3.
On pose u = 3x+4 et v = x2+1 ; u' = 3 et v' = 2x.
(u'v-v'u) / v2 =[3(x2+1)-2x(3x+4) ] / (x2+1)2 =(3x2+3-6x2-8x) / (x2+1)2 =(-3x2-8x+3) / (x2+1)2 . Réponse c.
4. Le plan est rapporté à un repère orthonormé.
L'ensemble des points 𝑀(x; y) tels que x2 + y2 − 10x + 6y + 30 = 0 est :
a) une droite ; b) une parabole ; c) un cercle ; d) ni une droite, ni une parabole, ni un cercle.
Réponse c.
x2 + y2 − 10x + 6y + 30 =x2 -10x+25-25 + y2 + 6y +9-9+ 30=(x-5)2 +(y+3)2-4=0.
(x-5)2 +(y+3)2= 4. Cercle de centre (5 ; -3) et de rayon 2.
5. La somme 1 + 5 + 52 + 53 + … + 530 est égale à :
a) (1-530) / 4 ; b) (530-1) / 4 ; c) (1-531) /4 ; d) (531-1) / 4.
Somme des termes d'une suite géométrique de raison 5 et de premier terme1.
(1-531) / (1-5)=(531-1) / 4.
Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 39. 1. Soit la fonction f définie sur l’intervalle [0; +∞[ par f(x) = x2- 3x + 4.
Etudier les variations de f sur [0; +∞[.
f '(x) =2x-3.
Si x < 1,5 , f '(x) est négative et f(x) est strictement décroissante.
Si x > 1,5 , f '(x) est positive et f(x) est strictement croissante.
Si x = 1,5, f '(x) est nulle et f(x) présente un minimum.
2. Dans un repère orthonormé, on considère la courbe c représentant la fonction racine carrée et le point A(2 ; 0).
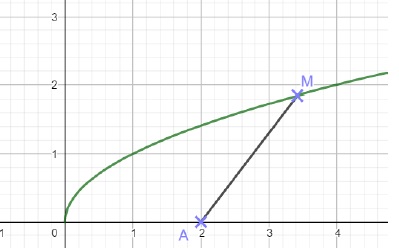
a) Soit M(x ; y) un point de c. Exprimer y en fonction de x.
y = x½.
b) En déduire que AM2=x2- 3x+4.
AM2 = (xM-xA)2 +(yM-yA)2=(x-2)2+y2 =x2+4-4x+x=x2- 3x+4.
c) Déterminer les coordonnées du point de c le plus proche de A. Ce point est noté B pour la suite.
L'abscisse de B est l'abscisse du minimum de la parabole d'équation y =x2- 3x+4.
B( 1,5 ; 1,5½).
d) Un élève affirme que la tangente en B à c est perpendiculaire au segment [AB]. A-t-il raison ? Justifier.
y ' =0,5 x-½ ; coefficient directeur de cette tangente : y '(1,5) = 0,5 / 1,5½.
Coefficient directeur de la droite (AB) : (yB-yA) /(xB-xA) =1,5½ / (-0,5) =-2*1,5½.
Le produit de ces deux coefficients directeurs étant égal à -1, la tangente à c en B est perpendiculaire au segment [AB].
Sujet 40.
Une
enquête a été réalisée auprès des élèves d'un lycée afin de connaître
leur point de vue sur la durée de la pause méridienne et sur les
rythmes scolaires.
L'enquête révèle que 55 % des élèves sont favorables à une pause méridienne plus longue.
Parmi ceux qui sont favorables à une pause méridienne plus longue, 95 %
souhaitent une répartition des cours plus étalée sur l'année scolaire.
Parmi ceux qui ne sont pas favorables à une pause méridienne plus
longue, seulement 10 % souhaitent une répartition des cours plus étalée
sur l'année scolaire.
On tire au hasard le nom d’un élève du lycée.
On considère les événements suivants :
L : « L'élève concerné est favorable à une pause méridienne plus longue. »
C: « L'élève concerné souhaite une répartition des cours plus étalée sur l'année scolaire. ».
1. Recopier et compléter l'arbre pondéré ci-dessous décrivant la situation.
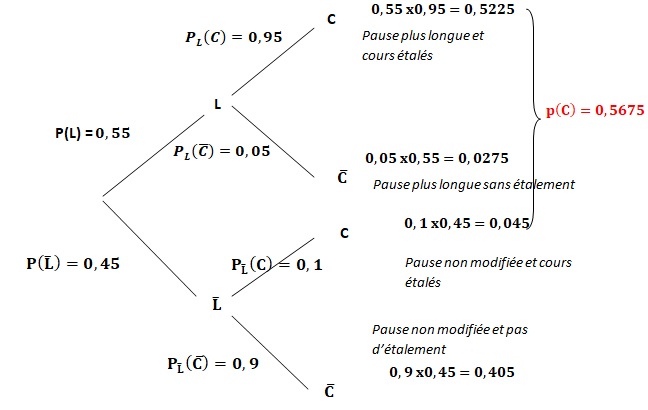
2. Calculer la
probabilité que l'élève concerné soit favorable à une pause méridienne
plus longue et souhaite une répartition des cours plus étalée sur
l'année scolaire.
0,55 x0,95 = 0,5225.
3. Montrer que p(C) = 0,5675.
4. Calculer la
probabilité que l'élève concerné soit favorable à une pause méridienne
plus longue sachant qu'il souhaite une répartition des cours plus
étalée sur l'année scolaire.
En donner une valeur arrondie à 10−4.
PC(L) = p(C n L) / p(C) =0,5225 / 0,5675 ~0,9207
5. Les événements L et C sont-ils indépendants ? Justifier la réponse.
P(L) = 0,55 ; p(C) =0,5675 ; p(L) x p(C) =0,312125 diffère de p(L n C).
Ces événements ne sont pas indépendants.
|
|
Exercice 3. ( 5 points).
Sujet 39.
Une
balle est lâchée d’une hauteur de 3 mètres au-dessus du sol. Elle
touche le sol et rebondit. À chaque rebond, la balle perd 25 % de sa
hauteur précédente.
On modélise la hauteur de la balle par une suite (hn) où hn désigne la hauteur maximale de la balle, en mètres, après le n-ième rebond. On a donc h0=3.
1. Calculer h1 et h2.
h1 = 3 x(1-25 /100) = 3 *0,75 = 2,25.
h2 = 2,25 *0,75 =1,6875.
2. La suite (hn) est-elle arithmétique ? Justifier.
hn+1-hn =0,75 hn-hn = -0,25 hn, diffère d'une constante : la suite n'est pas arithmétique.
3. Donner la nature de la suite (hn) en précisant ses éléments caractéristiques.
hn+1/ hn =0,75; suite géométrique de raison 0,75 et de premier terme h0 =3.
4. Déterminer la hauteur, arrondie au cm, de la balle après 6 rebonds.
h6 = h0 * 0,756 =3 *0,756 ~0,534 m.
5. La fonction « seuil » est définie ci-dessous en langage Python.
La recopier et la compléter pour que cette fonction renvoie le
nombre de rebonds à partir duquel la hauteur maximale de la balle sera
inférieure ou égale à 10 cm.
def seuil () :
h =3
n=0
while h >0,1
h = 0,75*h
n=n+1
return n.
Sujet 40.
À
l’issue d’une étude conduite pendant plusieurs années, on modélise
l'évolution du prix du m² d'un appartement neuf dans une ville
française de la manière suivante :
À partir d'un prix de 4 200 € le m² en 2019, on applique chaque année une augmentation annuelle de 3 % .
1. Avec ce modèle, montrer que le prix du m² d'un appartement neuf dans cette ville en 2021 serait de 4 455,78 €.
En 2020: 4200 x(1+3/100) = 4200 x1,03 =4326.
En 2021 : 4326 x1,03 =4 455,78.
2. On considère la suite de terme général un qui permet d’estimer, avec ce modèle, le prix en euro du m² d'un appartement neuf l'année 2019 + n𝑛. On a donc u0 = 4 200.
a) Quelle est la nature de la suite (un) ? En préciser la raison.
un+1 / un = 1,03, suite géométrique de raison 1,03 et de premier terme 4200.
b) En déduire l'expression du terme général un en fonction de n, pour tout entier naturel n.
un =4200 x1,03n.
c) Selon ce modèle, pourra-t-on acheter en 2024, un appartement de 40 m² si l'on dispose d'une somme de 200 000 € ?
En 2024 : u5=4200 x1,035=4868,95 € le m2.
4868,95 x 40 =194 758 €, valeur inférieure à 200 000 €. Réponse oui.
3. On définit, en langage Python, la fonction seuil ci-dessous.
def seuil() :
u =4200
n=0
while u < 8000 :
u =u*1,03
n=n+1
return n.
Recopier et compléter le programme de sorte que cette fonction renvoie
le nombre d'années nécessaires pour que, selon ce modèle, le prix du m²
d'un appartement neuf
dépasse 8 000 €.
|
|
Exercice 4. ( 5 points) Sujet 39 Une enquête réalisée dans un camping a donné les résultats suivants :
60 % des campeurs viennent en famille, les autres viennent entre amis ;
parmi ceux venant en famille, 35 % profitent des activités du camping ;
parmi ceux venant entre amis, 70 % ne profitent pas des activités du camping.
On choisit au hasard un client de ce camping et on considère les événements suivants :
F : « le campeur choisi est venu en famille »,
A : « le campeur choisi profite des activités du camping ».
1. Recopier et compléter l’arbre de probabilités donné ci-dessous :
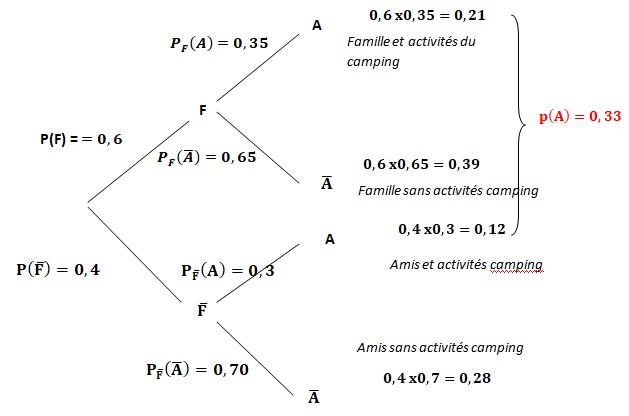
2. a) Calculer p(F∩ non A)
b) Interpréter ce résultat dans le contexte de l’exercice.
p(F∩ non A)=0,6 * 0,65 = 0,39.
39 % des campeurs viennent en famille sans profiter des activités du camping.
3. Montrer que p(A)=0,33.
4. Sachant que le
campeur choisi a profité des activités du camping, calculer la
probabilité qu’il soit venu en famille. Arrondir le résultat au
centième.
pA(F) = p(A n F) / p(A) =0,21 / 0,33 ~0,64.
|
Sujet 40.
1. Soit f la fonction définie sur R par f(x) = 4x3 − 48x2 + 144x.
a) Calculer f ′(x) et montrer que f ′(x) = 12(x2 − 8x + 12).
b) En déduire le tableau variations de la fonction f sur R.
f '(x) = 12x2 -96x+144 = 12(x2-8x+12).
Solutions de x2-8x+12=0 : discriminant D =(-8)2 -4 *12=16 = 42.
x1 = (8+4) / 2 = 6 et x2 =(8-4) / 2=2.
f '(x) = 12(x-2)(x-6).
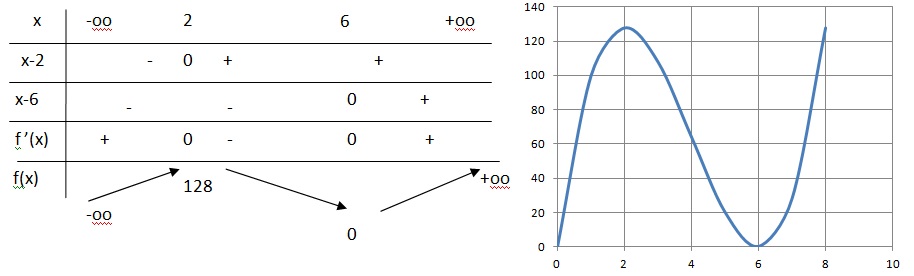
2.
Dans une plaque de carton carrée de 12 cm de côté, on découpe, aux
quatre coins, des carrés identiques afin de construire une boîte sans
couvercle, comme indiqué sur les figures
ci-dessous.
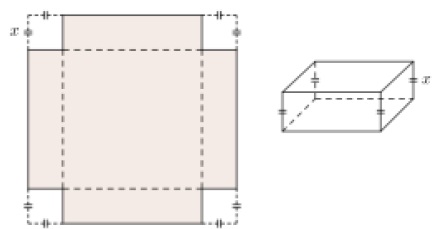
On note x la longueur (en cm) du côté de chacun des carrés découpés.
On admet que x ∈]0; 6[. L'objectif est de déterminer la longueur x permettant d'obtenir une boîte de volume maximal.
a) Montrer que le volume de la boîte est égal à 100 cm3 pour 𝑥 = 1. Détailler le calcul.
Aire du fond de la boîte : (12-2x)2 ; volume de la boîte : V =x(12-2x)2 ; si x = 1 V = (12-2)2 = 100 cm3.
b) Montrer que, pour x ∈]0; 6[, le volume de la boîte est égal à f(x), f étant la fonction étudiée à la question 1.
V = x(12-2x)2 = x(144+4x2-48x) =144x+4x3-48x2 = f(x).
c) Quelle est la valeur de x permettant d'obtenir une boîte de volume maximal ?
f(x) admet un maximum pour x = 2 et le volume est égal à 128 cm3.
.
|
|