Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 41
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1.Dans
un repère orthonormé, on donne les coordonnées de deux vecteurs soit
respectivement (-4 ; 3) et (-1 ; 5). Le produit scalaire de ces
deux vecteurs vaut :
a) −23 ; b) −17 ; c) 19 ; d) 23.
-4 *(-1) + 3 *5 = 19. Réponse c.
2. Dans un repère orthonormé, on donne les coordonnées d'un vecteur soit (-1 ; 5). Alors la longueur de ce vecteur est égale à :
a) 24 ; b) √24 c) 26 ; d) √26.
[(-1)2 +52)]½ =26½. Réponse c.
3.ABC est un triangle équilatéral de côté 3. I et H sont les milieux respectifs de [CB] et de [AB].
D est le projeté orthogonal de I sur (CH). On a :
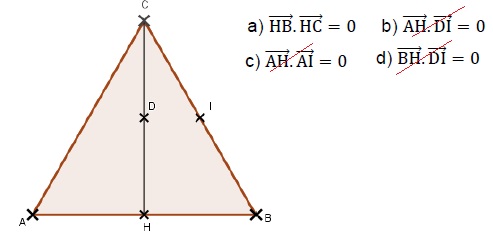
Réponse a.
4. Soit un réel 𝑥 tel que cos (x)=3½ / 2. On a :
a) cos (-x)=3½ / 2. cos (x)=3½ / 2.Vrai. ( la fonction cosinus est paire)
b) sin (x)= -3½ / 2.
c) sin (x)=3½ / 2.
d) cos (-x)= -3½ / 2.
Réponse c.
5. Le plan est muni d’un repère orthonormé.
On considère l’équation de cercle x2−2x+(y+3)2=3. Son centre a pour coordonnées :
a) (−1;−3) ; b) (1;−3) ; c) (−2;3) ; d) (−2;−3).
x2−2x+1-1+(y+3)2=3.
(x-1)2+(y+3)2=4.
Réponse b.
Sujet 42.
1. On considère la fonction g définie sur ℝ par g(x)=2x2+5x−4.
La tangente à la courbe représentative de g au point d’abscisse 2 a pour équation :
a) y=14x+14 ; b) y=14x−14 ; c) y=13x−15 ; d) y=13x−12. Réponse d.
f '(x) =4x+5.
Coefficient directeur de la tangente f '(2) =4*2+5=13.
La droite passe par le point de coordonnées (2 ; f(2) soit (2 ; 14).
14 = 13*2+b ; b = -12.
Equation de la tengente : y = 13x-12.
2. On se place dans un repère orthonormé du plan. On considère les points A(4;8), B(9;6) et D(2;11). Alors 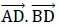 est égal à : est égal à :
a) −1 ; b) 11; c) −31; d) 29.Réponse d.
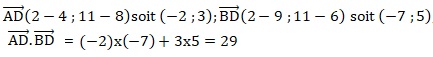
3.
Dans un repère orthonormé du plan, on considère la droite D d’équation
3x−4y+5=0. La droite parallèle à D et passant par A(4;8) a pour
équation :
a) 4x+3y−40=0 ; b) 3x−4y−5=0 ; c) 3x−4y+20=0 ; d) 4x+3y+6=0. Réponse c.
Les droites parallèles ont même vecteur directeur :
3x−4y+d=0.
A(4 ; 8) appartient à la droite : 3*4 - 4*8+d = 0 ; d =20.
4. Soit (un) la suite géométrique de raison q=−1,2 et de terme initial u0=10. Alors :
a) 0<u3000<1000 ; b) u3000=−3590 ; c) u3000 >1000 ; d) u3000=−36000.
u3000 = u0 * (-1,2)3000 ~3,497 x 10238.
Réponse c.
5. Soit (vn) la suite définie par : v0=1 et vn+1=4vn+2 pour tout entier n.
On veut déterminer la plus petite valeur de n telle que vn est supérieur ou égal à 100 000. On réalise pour cela le programme incomplet ci-dessous écrit en langage Python :
def algo( ) :
V = 1
n = 0
while ……………… :
n = n+1
V = 4* V + 2
return(n)
Pour que le programme retourne la valeur demandée, il faut compléter la partie en pointillé par :
a) V == 100000 ; b) V ! = 100000 ; c) V > 100000 ; d) V < 100000
Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 41. Au
sein d’un lycée, parmi les élèves de première ayant choisi la
spécialité mathématique, il y a 110 filles dont 5 ne poursuivent pas la
spécialité en terminale et 90 garçons dont 8 ne poursuivent pas la
spécialité.
On interroge au hasard un élève et on définit les événements suivants :
F l'événement : « L'élève interrogé est une fille »,
G l'événement : « L'élève interrogé est un garçon »,
S l'événement : « L'élève interrogé poursuit la spécialité ».
On donnera les valeurs exactes pour chacune des questions.
1) Calculer p(G), p(G∩S̅) et p(S̅).
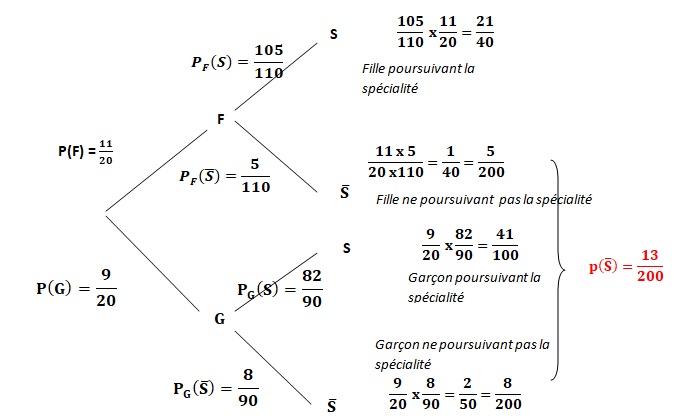
2) L'élève interrogé ne poursuit pas la spécialité. Calculer la probabilité que ce soit un garçon.
Pnon S (G) =P(non S n G) / P(non S) =8 / 13.
3) Les événements G et S sont-ils indépendants ?
P(G) x P(S) = 9 / 20 x 187 / 200 = 1683 / 4000.
P(G∩S) =41 / 100 différent de P(G) x P(S).
Ces événements ne sont pas indépendants.
Sujet 42.
Un fromager fait l’inventaire des produits qu’il a en cave.
La répartition de ses 3 types de fromages est : 25 % au lait de chèvre, 60 % au lait de vache, 15 % au lait de brebis.
Chacun de ses 3 types de fromages se partage en deux catégories : frais ou affiné.
Le tableau suivant donne la répartition des fromages de chaque catégorie suivant leur affinage :
|
frais
|
affiné
|
lait de vache
|
20 %
|
80 %
|
lait de chèvre
|
40 %
|
60 %
|
lait de brebis
|
70 %
|
30 %
|
Le fromager prend un fromage au hasard. On note les événements suivants :
V : « le fromage est fait avec du lait de vache » ;
C : « le fromage est fait avec du lait de chèvre » ;
B : « le fromage est fait avec du lait de brebis » ;
F : « le fromage est frais » ;
A : « le fromage est affiné ».
1) Donner les probabilités PC(A) et P(B).
2) Démontrer que P(A)=0,675.
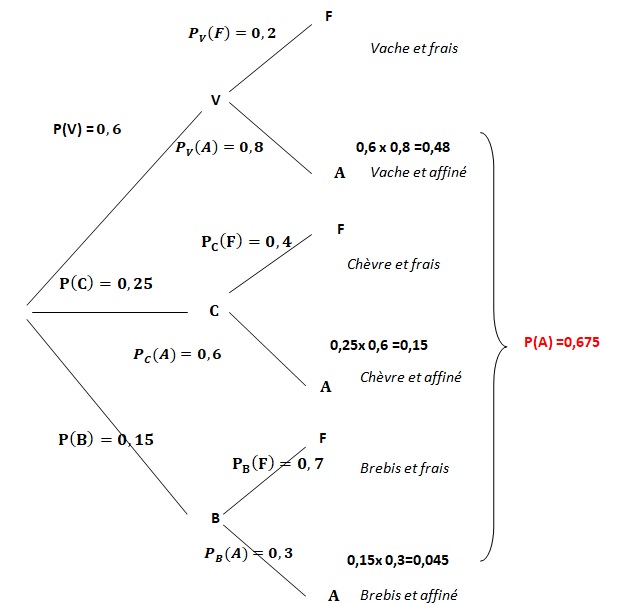
3) Le fromager
prend au hasard un fromage affiné. Quelle est la probabilité qu’il
s’agisse d’un fromage au lait de vache ? On donnera le résultat à 10−3 près.
PA(V) =P(A n V) / P(A) =0,48 / 0,675 ~0,711.
|
|
Exercice 3. ( 5 points).
Sujet 41.
Partie A.
Soit la suite géométrique (un) de raison 0,999 et de premier terme u0=82695.
1) Calculer u19.
u19 = u0 x0,99919 =82695 x0,99919 ~81 137, 856.
2) Calculer S=u0+u1+⋯+u19.
S = u0(1-0,99920) /(1-0,999) ~1 638 281,82.
Partie B.
La population d’un pays s’élevait à 82 695 000 habitants au premier janvier 2016.
Sans tenir compte des flux migratoires, on estime que la population baisse de 0,1 % chaque année.
Déterminer une estimation de l’effectif de la population de ce pays au premier janvier 2035.
0,1 % = 0,001.
Il s'agit d'une suite géométrique de raison 1-0,001 = 0,999 et de premier terme 82 695 000.
2035-2016 =19.
Estimation de la population en 2035 : 81 137 856.
Partie C.
Dans cette partie, on tient compte des flux migratoires : on estime
qu’en 2016, le solde migratoire (différence entre les entrées et les
sorties du territoire) est positif et s’élève à 58 700 personnes.
De plus, on admet que la baisse de 0,1 % de la population ainsi que le
solde migratoire restent constants chaque année suivant 2016.
On propose la fonction suivante écrite sous Python :
def population(N) :
p =82695000
for I in range (1, N+1):
p = 0,999*p+58700
return p
1) Si on saisit : « population (2) », quelle valeur nous retourne cette fonction ?
p1 = 0,999*82695000 + 58700 =82 671 005.
p2 = 0,999*82671005 + 58700 =82 647 034.
2) Si on saisit : « population (19) », la valeur arrondie à l'entier retournée par cette fonction est 82 243 175.
Que représente ce nombre dans le contexte de la partie C ?
En 2035, la population est estimée à 82 243 175 personnes.
Sujet 42.
Partie A.
Étudier sur ℝ le signe de P(x)=−10x2−40x+120.
Discriminant de −10x2−40x+120 = 0 ; D = (-40)2 -4*(-10)*120 =6400 =802.
Solutions de P(x) = 0 : x1 =(40 +80) / (-20) = -6 ; x1 =(40 -80) / (-20) = 2.
P(x) > 0 si x appartient à [-6 ; 2 ] et P(x) < 0 si x < 2 et x < -6.
Partie B.
On se place dans un repère orthonormé. La courbe H représentée sur le
graphique ci -dessous est l’ensemble des points de l’hyperbole
d’équation : y=(10x+4) / (x+2)
avec x appartenant à l’intervalle [0 ; 8].
Pour toute abscisse x dans l’intervalle [0 ; 8], on construit le
rectangle ABDE comme indiqué sur la figure. On donne les informations
suivantes :
A et B sont sur l’axe des abscisses ;
A est d’abscisse x ;
B et D ont pour abscisse 8 ;
E appartient à la courbe H ;
D et E ont la même ordonnée.
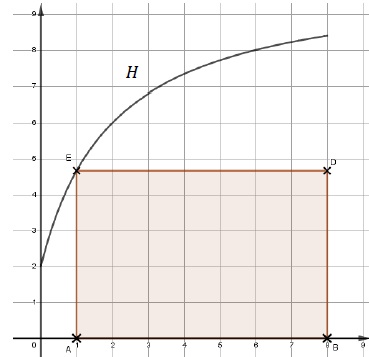
L’objectif de ce problème est de déterminer la ou les valeurs
éventuelles x de l’intervalle [0 ; 8] correspondant à un rectangle ABDE
d’aire maximale.
1) Déterminer l’aire du rectangle ABDE lorsque x = 0.
AB = 8 ; AE = 2 ; aire du rectangle : 8 * 2 = 16.
2) Déterminer l’aire du rectangle ABDE lorsque x = 4.
AB = 4 ; AE =44 / 6 = 22 /3 ; aire du rectangle : 4 *22 /3 = 88 /3.
On définit la fonction f qui à tout réel x de [0 ; 8], associe l’aire du rectangle ABDE. On admet que : f(x)=(−10x2+76x+32) / (x+2).
3) Répondre au problème posé.
Calcul de f '(x) en posant u = −10x2+76x+32 et v = x+2; u' = -20x +76 ; v' = 1.
(u'v-v'u) / v2 =[(-20x+76)(x+2)-(−10x2+76x+32)] /(x+2)2 =[-20x2-40x +76x +152+10x2-76x-32)] /(x+2)2 =[-10x2-40x +120] /(x+2)2 .
f ' (x) possède le signe de -10x2-40x +120 :
f '(x) >0 si x appartient à [2 ; 8] et f(x) est
croisante ; f ' (x) < 0 si x appartient à [0 ; 2] et f(x) est
décroissante.
L'aire du rectangle est maximale pour x = 2.
|
|
Exercice 4. ( 5 points) Sujet 41 On considère la fonction f définie sur ]−∞;2[ par : f(x) = (x2-4x+8) / (x-2).
On se place dans un repère orthonormé.
1) Résoudre f(x) = 0.
x2-4x+8 =0 ; discriminant D =(-4)2 -4*8= -16.
Le discriminant étant négatif, il n'y a pas de solution réelle.
2) On note f ′ la fonction dérivée de f.
a. Démontrer que pour tout réel x de ]−∞;2[ : f ′(x)=(x2−4x) / (x−2)2.
On pose u = x2-4x+8 et v = x-2 ; u' = 2x-4 ; v ' = 1.
(u ' v- v 'u) / v2 = [(2x-4)(x-2)-( x2-4x+8)] /(x-2)2 =[2x2-4x-4x+8-x2+4x-8)] / (x-2)2 =(x2−4x) / (x−2)2.
b. Déterminer les variations de la fonction f.
Le signe de f '(x) est celui de x2-4x = x(x-4).
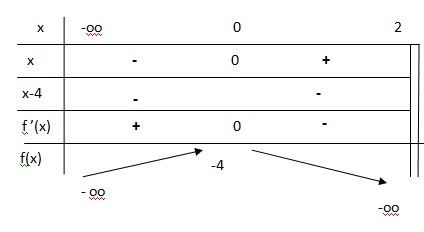
3) Déterminer une équation de la tangente D à la courbe représentative de f au point d’abscisse 1.
Coefficient directeur de cette droite : f '(1) = -3.
La tangente passe par le point de coordonnée (1 ; f(1)) soit (1 ; -5).
-5 = -3+b ; b = -2. y = -3x-2.
4) Tracer la droite D et une esquisse de la courbe représentative de la fonction f dans le repère donné.
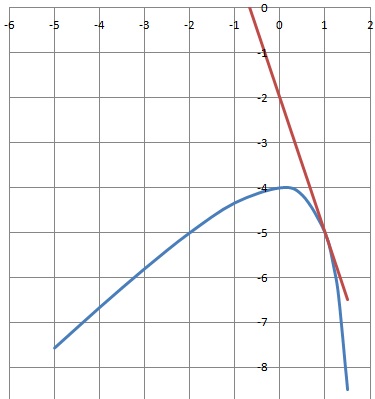
|
Sujet 42.
On applique une tension sinusoïdale u aux bornes d’un circuit électrique comportant en série une résistance et une diode idéale.
Le temps t est exprimé en seconde.
La tension est donnée par la fonction u définie pour tout réel t ≥0 par : u(t)=3½ sin(100p t+p/3)
La diode est non passante si u(t)≤ 3½ / 2 et elle est passante si u(t) > 3½ / 2.
1) La diode est-elle passante à l’instant t=0 ?
u(0) =3½ sin(p/3)=1,5.
u(0) > 3½ / 2, la diode est passante.
2) Calculer u(0,01). Interpréter le résultat.
u(0,01)=3½ sin(100p *0,01+p/3) =3½ sin(4p /3) = -1,5.
u(0,01) < 3½ / 2, la diode est non passante.
3) On admet que u(t+0,02)=u(t) pour tout t ≥0. En déduire une propriété de la fonction u.
u(t) est périodique de période 0,02 s.
4) On donne ci-dessous la courbe représentative de la fonction u sur l’intervalle [0;0,02] :
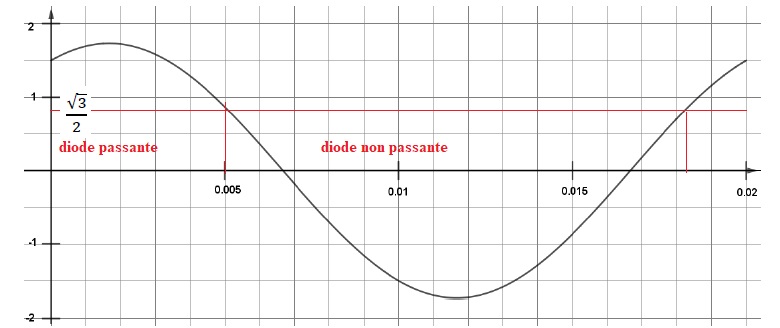
On cherche à savoir au bout de combien de temps la diode devient non passante pour la première fois.
a. Conjecturer la solution du problème à l’aide du graphique.
b. Calculer u(0,005) et conclure.
u(0,005)=3½ sin(100p *0,005+p/3) =3½ sin(5p /6) = 3½ / 2.
.
|
|