Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 43
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1.On définit la fonction f sur ]2,5 ;+∞[ par : f(x)=(3x+1) / (−2𝑥+5)
Alors pour tout x∈]2,5;+∞[, f ′(x) est donné par l’expression :
a) -1,5 ; b) 17/(−2𝑥+5)² ; c) 13 /(−2𝑥+5)² : d) −13(−2𝑥+5)² Réponse b.
On pose u = 3x+1 et v = -2x+5 ; u' = 3 ; v' = -2.
(u'v-v'u) / v2 =[3(-2x+5)-(-2)(3x+1)] / (-2x+5)2 =17 / (-2x+5)2 .
2.
On considère une fonction f polynôme de degré 2 dont une représentation
graphique est donnée ci dessous dans un repère orthonormé.
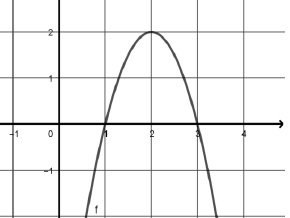
Par lecture graphique, on peut affirmer qu’une forme factorisée de 𝑓 est :
a) −2(x+1)(x+3)
b) −2(x−1)(x−3)
c) 2(x−1)(x−3)
d) 2(x+1)(x+3) Réponse b.
3. On
se place dans un repère orthogonal. On a tracé ci dessous la courbe
représentative d’une fonction 𝑓 ainsi que sa tangente au point A.
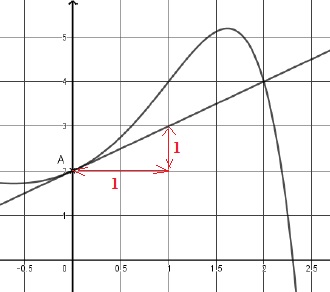
On a alors :
a) f ′(0)=0 ; b) f ′(0)=2 ; c) f ′(0)=1 ; d) f ′(0)=0,5
Réponse c.
4. Le plan est rapporté à un repère orthonormé. On considère les points G(1 ;−2) et H(6 ;4).
La droite (GH) passe par le point :
a) A(−3 ;2) ; b) B(2,5 ;0) ; c) C(10 ;12) ; d) D(−14 ;−20).
Réponse d.
y = ax+b.
G appartient à cette droite : -2 =a+b ; H appartient à cette droite : 4=6a+b.
4-(-2) =6a-a ; a = 6 /5 =1,2 et b = -3,2.
y = 1,2x -3,2.

5.On considère un nombre réel x appartenant à l’intervalle [𝜋 ; 3𝜋/2] tel que cos x =− √3 /2.
Alors sin(x) est égal à :
a) √3 / 2 ; b) −√3 / 2 ; c) −1 / 2; d) 1 / 2.
Réponse c.
sin2 x = 1 -cos2x = 1-3 /4 = 1 /4 ; sin x = ±1 / 2.
x appartient à l’intervalle [𝜋 ; 3𝜋/2] , solution retenue sin x = -1 / 2.
Sujet 44.
1. cos(𝑥)=−√3 / 2 pour :
a) 𝑥=5𝜋 / 6 ; b) 𝑥=4𝜋 / 3 ; c) 𝑥=−𝜋 / 3 ; d) 𝑥=−𝜋 / 6. Réponse a.
cos x = ± cos (5𝜋 / 6).
2. Dans
le plan muni d’un repère, on considère la droite (AB) passant par les
points A(−2,7) et B(4,−5) Un vecteur directeur de la droite (AB) a pour
coordonnées :
a) (2 ; 2) ; b) (−12 ; 6) ; c) (6−12) ; d) (2 ; −12). Réponse c.
y = ax +b.
A appartient à la droite : 7 =-2a+b ; B appartient à la droite : -5 = 4a+b.
-5-7=4a-(-2a) ; a = -2.
Coordonnées d'un vecteur directeur de cette droite : (1 ; -2) ou (6 ; -12)
3. Dans le plan muni d’un repère, la droite d’équation 𝑦=−2𝑥+5 a pour vecteur directeur, le vecteur de coordonnées :
a) (2 ; 1) ; b) (−1 ; 2) ; c) (1 ; 2) ; d) (−2 ; 1). Réponse b.
Coordonnées d'un vecteur directeur de cette droite : (1 ; -2) ou ( -1 ; 2).
4. Dans le plan muni d’un repère, la représentation graphique d’une parabole P est donnée ci-dessous. La forme canonique
de son équation est :
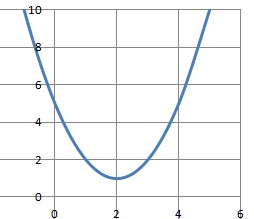
a) 𝑦 = (𝑥 + 2)2 + 5 ; b) 𝑦 = (𝑥 − 5)2 + 1 ;
c) 𝑦 = (𝑥 − 1)2 + 2 d) 𝑦 = (𝑥 − 2)2 + 1.
Réponse d.
5. Soit le cercle d’équation cartésienne (𝑥 + 2)2 + (𝑦 − 3)2 = 9 dans le plan muni d’un repère orthonormé :
a) le cercle a pour centre C(−2, 3)
b) le cercle a pour centre C(3, −2)
c) le cercle a pour rayon 𝑅 = 9²
d) le cercle a pour centre C(2, −3)
Réponse a.
|
|
Exercice 2. ( 5
points) Sujet 43. Camille
et Dominique ont été embauchés au même moment dans une entreprise et
ont négocié leur contrat à des conditions différentes :
- Camille a commencé en 2010 avec un salaire annuel de 14 400 €, alors
que le salaire de Dominique était, cette même année, de 13 200 €.
- Le salaire de Camille augmente de 600 € par an alors que celui de Dominique augmente de 4 % par an.
1) Quels étaient salaires annuels de Camille et Dominique en 2012 ?
14400 +600+600=15 600 €.
13200 x1,042 =14 277,12 €.
2) On modélise les salaires de Camille et de Dominique à l’aide de suites.
a. On note un le salaire de Camille en l’année 2010 +n. On a donc u0= 14 400.
Quelle est la nature de la suite (𝑢n) ?
Suite arithmétique de raison 600, de premier terme 14 400.
b. Déterminer en quelle année le salaire de Camille dépassera 20 000 €.
un = 14 400 + 600 n > 20 000 ; 600 n > 5600 ; n > 5600 / 600 ; n > 9,33 soit 10 ( année 2020 ).
c. On note 𝑣𝑛 le salaire de Dominique en l’année 2010 +𝑛.
Exprimer 𝑣𝑛+1 en fonction de 𝑣𝑛.
vn+1 = 1,04 vn.
d. Calculer le salaire de Dominique en 2020. On arrondira le résultat à l’euro.
v10 = 13200 *1,0410 ~19539.
3) On veut
déterminer à partir de quelle année le salaire de Dominique dépassera
celui de Camille. Pour cela, on dispose du programme incomplet ci
dessous écrit en langage Python.
Recopier et compléter les quatre parties en pointillé du programme ci dessous :
def algo() :
A = 14400
B = 13200
n=0
while : B < A
A = A+600
B = B*1,04
n =n+1
return (n)
Sujet 44.
Soit la fonction 𝑝 définie sur 𝑹 par 𝑝(𝑥) = −𝑥3 + 3𝑥2 + 9𝑥 + 5.
Partie A :
1. Quelle est l’image de 5 par 𝑝 ?
p(5) = -53 +3*52 +9*5+5= 0
2. Montrer que pour tout réel 𝑥, 𝑝(𝑥) = (5 − 𝑥)(𝑥2 + 2𝑥 + 1).
(5 − 𝑥)(𝑥2 + 2𝑥 + 1) =5x2 +10x +5-x3-2x2-x =−𝑥3 + 3𝑥2 + 9𝑥 + 5 = p(x)
3. En déduire le signe de 𝑝(𝑥) sur 𝑹.
p(x) = (5-x)(x+1)2.
(x+1)2 est positif, le signe de p(x) est celui de (5-x).
Si x < 5, p(x) positif ; si x=5, p(x) = 0 ; si x > 5, p(x) négatif.
Partie B :
1. Déterminer la fonction dérivée de la fonction 𝑝.
2. Démontrer que la fonction 𝑝 admet un maximum sur l’intervalle [0;5] dont on précisera la valeur.
p '(x) = -3x2 +6x +9 = 3(-x2 +2x+3).
Racines de -x2 +2x+3 =0 ; discriminant D =22-4*3*(-1) =16 = 42.
x1 =(-2-4) / (-2) = 3 ; x1 =(-2+4) / (-2) = -1 ;
p'(x) < 0 sur ]-oo ; -1], p(x) décroissante.
p'(x) > 0 sur [-1 ;3], p(x) croissante.
p'(x) <0 sur [3 ; +oo[, p(x) décroissante.
p'(-1) = 0 ; p(x) présente un minimum pour x = -1.
p'(3) = 0 ; p(x) présente un maximum pour x =3
p(3) =-33 +3*32 +9*3+5= 32.
|
|
Exercice 3. ( 5 points).
Sujet 43.
Dans un repère orthonormé, on considère les points A(−1 ;3), B(5 ;0) et C(9 ;3).
1) Déterminer une équation cartésienne de la droite (AB).
y = ax +b.
A appartient à cette droite :3= -a+b ; B appartient à cette droite : 0 = 5a+b.
0-3=5a-(-a) ; a = -0,5 et b = 2,5.
y = -0,5x+2.5 soit y +0,5x-2,5=0.
2) Déterminer une équation cartésienne de la droite 𝐷 passant par le point C et de vecteur normal de coordonnées (-1 ; 3).
3y-x+b =0.
C appartient à cette droite : 3*3-9+b=0 ; b = 0 ; 3y-x=0.
3) Démontrer que les droites 𝐷 et (AB) ne sont pas parallèles.
Coefficient directeur de la droite (AB) : -0,5.
Coefficient directeur de la droite (D) : 1 /3.
Ces coefficient étant différents, les droites ne sont pas parallèles.
On admet que le point E(3 ;1) est le point d’intersection de ces deux droites.
4) Les droites 𝐷 et (AB) sont elles perpendiculaires ?
Coordonnées d'un vecteur normal à la droite (AB) : 0,5 ; 1.
Coordonnées d'un vecteur normal à la droite (D) : -1 ; 3.
Ces deux vecteurs ne sont pas perpendiculaires; leur produit scalaire n'est pas nul ( 0,5 *(-1)+3*1 =2,5, diffère de zéro).
Les droites ne sont pas perpendiculaires.
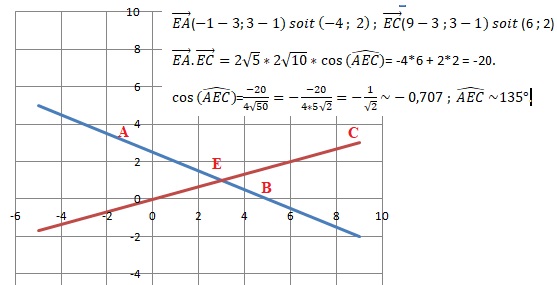
5) On donne AE=2√5 et EC=2√10.
Calculer la mesure en degrés de l’angle AEC.
Sujet 44.
Au cours de l’hiver, on observe dans une population, 12 % de personnes malades.
Parmi les personnes malades, 36 % d’entre elles pratiquent une activité sportive régulièrement.
Parmi les personnes non malades, 54 % d’entre elles pratiquent une activité sportive régulièrement.
Une personne est choisie au hasard dans la population.
On note M l’événement « la personne est malade » et S l’événement « la personne a une activité sportive régulière ».
Dans cet exercice, les résultats approchés seront donnés à 10 – 3 près.
1. Recopier et compléter l’arbre pondéré.
2.a) Quelle est la probabilité que la personne soit malade et qu’elle pratique une activité sportive régulièrement ?
b) Montrer que la probabilité que la personne pratique une activité sportive régulièrement est égale à 0,5184.
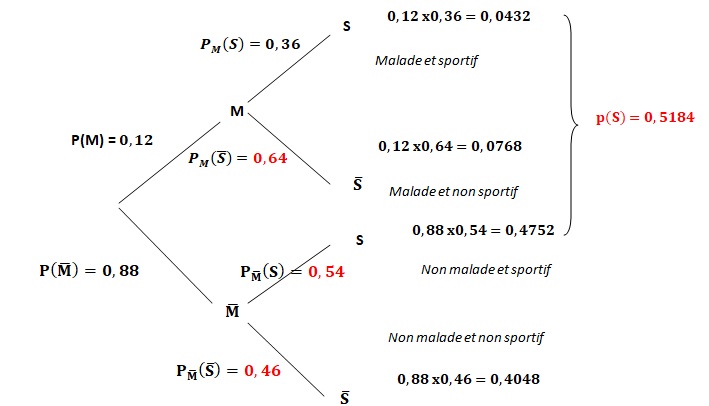
3. La personne choisie n’a pas d’activité sportive régulière. Quelle est la probabilité pour qu’elle soit malade ?
Pnon S (M) =P(non S n M) / P(non S) =0,0768 / (1-0,5184)~0,160.
4. Un journaliste
annonce qu’une pratique régulière d’une activité sportive diminue par
deux le risque de tomber malade. Que peut-on conclure sur la pertinence
de cette annonce ? Justifier.
P S (M) =P(S n M) / P( S) =0,0432 / 0,5184~0,0833.
P S (M) ~0,5 Pnon S (M), l'affirmation est vraie.
|
|
Exercice 4. ( 5 points) Sujet 43 Un parent d’élèves propose un jeu pour la fête de l’école.
Une urne opaque contient 100 billes indiscernables au toucher : 10 billes rouges, 30 billes blanches et 60 billes vertes.
Pour une partie, chaque joueur doit miser 2 jetons. Ensuite, le joueur prélève une bille au hasard dans l’urne.
Si la bille prélevée est rouge, le joueur récupère 8 jetons.
Si la bille est blanche, le joueur récupère 4 jetons.
Si la bille est verte, le joueur ne gagne rien.
On note X la variable aléatoire égale au gain algébrique du joueur en
nombre de jetons, c’est à dire, le nombre de jetons gagnés diminué de
la mise.
1) a) Établir que la loi de probabilité de X est donnée par :
valeurs prises par X
|
-2
|
2
|
6
|
P(X) =a
|
0,6
|
0,3
|
0,1
|
Probabilité de tirer une boule rouge : 10 /100 = 0,1. Gain :8-2 =6.
Probabilité de tirer une boule blanche : 30 /100 = 0,3. Gain :4-2 =2.
Probabilité de tirer une boule verte : 60 /100 = 0,6. Gain :0-2 = -2.
1) b) Démontrer que le jeu est équitable, c’est à dire que l’espérance de X est nulle.
-2 *0,6 +2 *0,3 +6*0,1 = 0.
1) c) Calculer la variance puis l’écart type de X. On arrondira au centième.
Variance : V = 0,6*(-2)2 +0,3 *22 +0,1*62 =2,4 +1,2 +3,6 =7,2 ; écart type : s = 7,2½ =2,68.
2) Pour financer
les différentes actions de l’école, les organisateurs de la fête
veulent modifier le jeu pour qu’il leur devienne favorable. Ils
décident alors d’ajouter des billes vertes dans l’urne.
Combien de billes vertes doit on ajouter dans l’urne pour que l’espérance du jeu soit égale à −1 ?
Soit x le nombre de billes vertes ajoutées dans l'urne.
Probabilité de tirer une boule rouge : 10 /(100+x) . Gain :8-2 =6.
Probabilité de tirer une boule blanche : 30 /(100+x) . Gain :4-2 =2.
Probabilité de tirer une boule verte : 60+x / (100+x) . Gain :0-2 = -2.
Espérance : E=[6*10 +2*30 -2(60+x)] / (100+x) = -1.
-2x /(100+x) = - 1 ; 2x = 100 +x ; x = 100.
|
Sujet 44.
En 2012, un artisan batelier a transporté 300 tonnes de marchandises sur sa péniche.
Il augmente sa cargaison chaque année de 11 % par rapport à l’année précédente.
On modélise alors la quantité en tonnes de marchandises transportées par l’artisan batelier par une suite (𝑢𝑛) où pour tout entier naturel 𝑛, 𝑢𝑛 est la quantité en tonnes de marchandises transportées en (2012 + 𝑛). Ainsi 𝑢0=300.
1. a) Donner la nature de la suite (𝑢𝑛) et préciser sa raison.
un+1 / un = 1,11, suite géométrique de raison 1,11.
b) Pour tout entier naturel 𝑛, exprimer 𝑢𝑛 en fonction de 𝑛.
un = 300 x 1,11n.
2. Le batelier décide qu’à partir de 1 000 tonnes transportées dans l’année, il achètera une péniche plus grande.
a) Recopier et
compléter l’algorithme suivant, écrit en langage Python, afin de
déterminer en quelle année il devra changer de péniche :
u =300
n=0
while u <1000 :
u = 1,11*u
n=n+1
b) En quelle année changera-t-il de péniche ?
u11 = 300 x 1,1111 =945 ; u12 = 300 x 1,1112 =1049. (année 2012+12=2024).
3. Une tonne transportée est payée au batelier 15 €.
La proposition : « Le chiffre d’affaires total entre 2012 et 2019 de
l’artisan batelier sera supérieur à 70 000 € » est-elle vraie ?
Justifier la réponse.
Somme des 8 premiers termes de la suite géométrique : 300(1-1,118) /(1-1,11) =3557,83.
3557,83 x15 =53 367 €, l'affirmation est fausse.
.
|
|