Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 47
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Soient
deux vecteurs de coordonnées respectives (–1 ;0) et (–3 ;4) dans un
repère orthonormé du plan. Alors le module de la différence de
ces deux vecteurs est égale à :
a. 4√2 b ; √32 ; c. 20 ; d. 2√5. Réponse d.
 . .
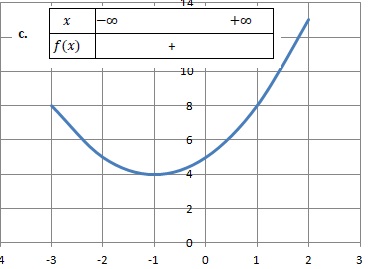
2. Le tableau de signes de la fonction polynôme définie sur R par 𝑓(𝑥)=𝑥2+2𝑥+5 est : Réponse c.
Racines de x2+2x+5=0 ; discriminant D =22-4*5 = -16 ; aucune racine réelles.
f(x) est positive sur l'ensemble des réels.
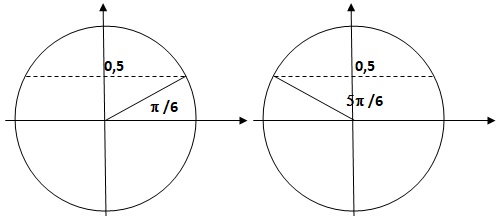
3. Sur l’intervalle ] –π ; π], l’équation sin(𝑥)=1 / 2 a pour solution(s)
a. 𝜋 /6 ; b. 𝜋 / 3 et 2𝜋 /3 ; c. −𝜋 /6 et 𝜋 /6 ; d. 𝜋/ 6 et 5𝜋 /6.
Réponse d.
4. On considère la suite (𝑢𝑛) définie par 𝑢0=15 et pour tout entier naturel 𝑛 : 𝑢𝑛+1=0,8 𝑢𝑛+1.
On a écrit la fonction suite() ci-dessous en langage Python.
def suite() :
n=0
u=15
while u >6
n=n+1
u=0,8*u+1
return n
L’appel de cette fonction renvoie :
a. Le plus petit entier n tel que un>6
b. Le plus petit entier 𝑛 tel que 𝑢𝑛 ≤ 6
c. Le premier terme de la suite tel que 𝑢𝑛 >6
d. Le premier terme de la suite tel que 𝑢𝑛 ≤ 6.
Réponse d.
5. Pour tout réel 𝑥, e3𝑥−5×e4−3𝑥 est égal à :
a. 1 /e ; b. e(3𝑥−5)×(4−3𝑥) ; c. e ; d. exp(−9𝑥2+27𝑥−20). Réponse a.
exp(3x-5 +4-3x) = exp(-1) = 1 / e.
Sujet 48.
1. 1. On considère une fonction 𝑓 définie et dérivable sur l’intervalle [−1 ; 4] .
On a tracé sur la figure ci-dessous la courbe 𝒞𝑓 et la tangente à cette courbe au point A de coordonnées (2 ; 2).
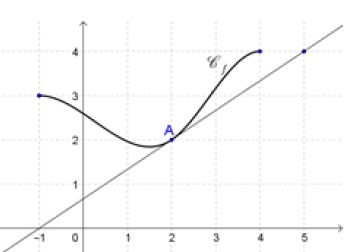
L’équation de la tangente à 𝒞𝑓 au point A est :
a. 𝑦 =2 / 3(𝑥−2)+2 ; b. 𝑦 = 2(𝑥−2)+2 / 3 ; c. 𝑦 =2 / 3(𝑥+2)+2 ; d. 𝑦 =3 / 2(𝑥−2)+2.
Coeficient directeur de la tangente en A : 4 / 6 = 2 /3.
A (2 ; 2) appartient à la tangente : 2 = 2 /3 *2+b ; b = 2 /3.
y =2x /3 +2 /3 = 2x /3 +4 /3-4 /3 +2 /3 = 2 /3 (x-2) +2. Réponse a.
2. Dans
un repère orthonormal (0,𝐼,𝐽), le point A, placé ci-contre sur le
cercle trigonométrique de centre O d’origine I , est associé au nombre
réel :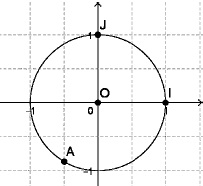
a. 11𝜋 / 6 ; b. 2𝜋 / 3 ; c. −2𝜋 / 3 ; d. −3𝜋 / 4. Réponse c.
3. On considère une fonction du second degré f définie sur R par :
𝑓 (𝑥)=𝑎𝑥2+𝑏𝑥
où 𝑎 et 𝑏 sont deux nombres réels strictement positifs.
Quelle est la courbe représentative de cette fonction dans un repère orthonormé ? Réponse d.
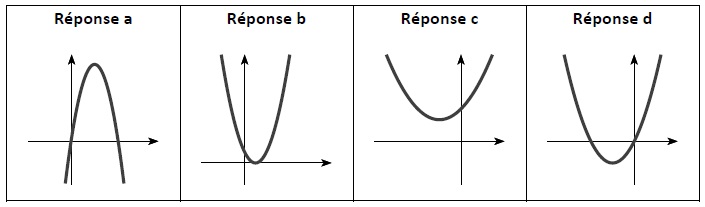
La parabole est symétrique par rapport à la droite d'équation x = -b / (2a), négatif et passe par l'origine.
4.
Dans le plan muni d’un repère orthonormé une droite 𝒟 a pour équation
: 𝑥−2𝑦=1 soit y = 0,5x -0,5. Parmi les propositions suivantes,
laquelle est correcte ?
a. Le vecteur de coordonnées (1 ; −2) est un vecteur directeur de la droite 𝒟.
b. Le vecteur de coordonnées(1 ; −2) est un vecteur normal à la droite 𝒟. Vrai
c. Le point de coordonnées 𝐴(1,−2) appartient à la droite 𝒟.
d. L’ordonnée à l’origine de la droite 𝒟 est égale à 1.
5. Un homme
marche pendant 10 jours. Le premier jour, il parcourt 12 km. Chaque
jour, il parcourt 500 m de moins que la veille. Durant ces dix jours,
il aura parcouru au total :
a. 95 km ; b. 97,5 km ; c. 19 km ; d. 84 km.
Réponse b.
12 +11,5 +11 +10,5 +10 +9,5 +9 +8,5 +8 +7,5 =97,5.
Somme des 10 premiers termes d'une suite arithmétique de raison -0,5, de premier terme 12.
(12+7,5) *5 = 97,5.
|
|
Exercice 2. ( 5
points) Sujet 47. Le
président d’un club de handball a constaté une augmentation du nombre
d’adhérents dans son club depuis 2016 (toutes catégories confondues).
En effet en 2016, il y avait 377 adhérents, 396 en 2017 et 416 en 2018.
Ce qui correspond à une hausse chaque année d’environ 5 %.
Il souhaite faire une estimation pour les années à venir, en supposant que cette hausse de 5 % par an se poursuit.
On modélise le nombre d’adhérents l’année 2018+𝑛 par la suite de terme général 𝑢𝑛.
On a donc 𝑢0 = 416.
1. Calculer 𝑢1 et 𝑢2. Arrondir les résultats à l’unité.
u1 = 416 *1,05 ~437 ; u2 = 416 *1,052 ~459.
2. Quelle est la nature de la suite (𝑢𝑛) ? Préciser son premier terme et sa raison.
un+1 / un = 1,05, suite géométrique de raison 1,05, de premier terme 416.
3. Exprimer 𝑢𝑛 en fonction de 𝑛, pour tout entier naturel 𝑛.
un = 416*1,05n.
4. Calculer 𝑢7. Interpréter ce résultat par rapport aux données de l’énoncé.
u7 = 416*1,057~585.
En 2018+7 soit en 2025, il y aura 585 adhérents.
5. À partir de quelle année le président du club peut-il espérer dépasser les 700 adhérents ?
416*1,05n > 700 ; 1,05n > 700 / 416 ; 1,05n >1,683 ; n > 11 ( 416 x1,0511 ~711 ). Année 2029.
Sujet 48.
Une
entreprise fabrique chaque jour 𝑥 tonnes d’un produit. Le coût total
mensuel, en milliers d’euros, pour produire chaque jour 𝑥 tonnes de ce
produit est modélisé par la fonction 𝐶 définie sur l’intervalle [0 ;
10] par : 𝐶(𝑥)= (5𝑥−2)e−0,2𝑥 +2
On a représenté ci-dessous la courbe 𝒞𝐶 de la fonction C dans un repère.
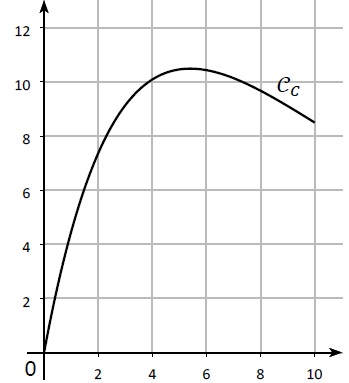
1. Par lecture
graphique, donner une estimation de la quantité journalière de produit
pour laquelle le coût total mensuel est maximal.
5,5 tonnes.
2. Le coût marginal 𝐶𝑚,
qui correspond au supplément de coût total pour la production d’une
unité de valeur supplémentaire, est assimilé à la dérivée de la
fonction coût total.
a) Démontrer que le coût marginal 𝐶𝑚 est défini sur l’intervalle [0 ; 10] par :
𝐶𝑚(𝑥)=(−𝑥+5,4)e−0,2𝑥.
On pose u = 5x-2 et v = e-0,2x ; u' = 5 ; v' = -0,2e-0,2x.
u'v+v'u = 5e-0,2x-0,2(5x-2)e-0,2x =(-x+5,4)e−0,2𝑥.
b) Pour quelle quantité de produit fabriqué par jour le coût marginal est-il négatif ?
e−0,2𝑥 >0 ; -x+5,4 < 0 soit x >5,4.
c) Donner le tableau de variations de la fonction 𝐶 sur l’intervalle [0 ;10].
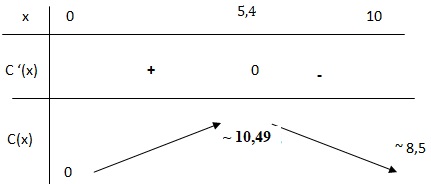
d) Déterminer le coût total mensuel maximal sur l’intervalle considéré. On donnera la valeur arrondie à l’euro près.
10 490 €
|
|
Exercice 3. ( 5 points).
Sujet 47.
Un artisan fabrique de la confiture qu’il vend à un grossiste. Le coût, en euros, de fabrication de 𝑥 kilos de confiture est :
𝐶(𝑥)=0,1𝑥2+0,7𝑥+100, pour 𝑥∈[0;160].
1. Chaque kilo est vendu 14 €. Exprimer la recette 𝑅 en fonction de 𝑥.
R = 14 x.
2. Soit 𝐵 la fonction représentant le bénéfice de l’artisan, définie sur [0;160].
𝐵 a pour expression 𝐵(𝑥)=−0,1𝑥2+13,3𝑥−100.
Étudier le signe de 𝐵(𝑥). En déduire l’intervalle dans lequel doit se
trouver le nombre de kilos de confiture à vendre pour que l’artisan
réalise un bénéfice positif.
Racines de -0,1x2+13,3x-100 = 0 : discriminant D =13,32-4*(-0,1)*(-100)=136,89=11,72.
x1 =(-13,3-11,7) /(-0,2) =125 ; x1 =(-13,3+11,7) /(-0,2) =8 ;
x doit appartenir à l'intervalle [ 8 ; 125].
3. On note B′ la fonction dérivée de la fonction B.
a. Déterminer 𝐵′(𝑥).
B'(x) = -0,2x +13,3.
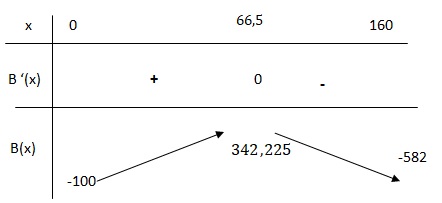
b. Dresser le tableau de variation de B sur l’intervalle [0;160].
c. Donner le nombre de kilos à vendre pour que le bénéfice soit maximal ainsi que son montant.
Sujet 48.
On considère qu’en 2019, 3 300 000 personnes étaient atteintes de diabète en France.
Pour étudier l’évolution de la maladie, des chercheurs appliquent un
modèle selon lequel le nombre de personnes atteintes augmente de 2 %
par an.
On note 𝑢𝑛 le nombre de personnes atteintes de diabète en France selon ce modèle durant l’année (2019+𝑛). On a donc 𝑢0=3 300 000.
1. Justifier que, selon ce modèle, le nombre de personnes atteintes de diabète en France sera de 3 433 320 en 2021.
En 2020 : 3 300 000 x1,02 =3 366 000 ; en 2021 : 3 366 000 x1,02 =3 433 320.
2. Quelle est la nature de la suite (un) ?
Suite géométrique de raison 1,02 et de premier terme 3 300 000.
3. Donner l’expression de un en fonction de 𝑛.
un = 3 300 000 x1,02n.
4. En déduire le nombre de personnes qui, selon ce modèle, seront atteintes de diabète en France en 2025.
u6 = 3 300 000 x1,026= 3 716 336.
5. On définit en langage Python la fonction suivante.
def seuil(S) :
u=3300000
n=0
while u < S:
u=u*1,02
n=n+1
return n.
Après exécution dans la console on obtient l’affichage suivant.
seuil(5000000)
21
Interpréter ce résultat dans le contexte de l’exercice.
En 2019+21 soit en 2040, le nombre de diabétiques dépasse 5 000 000.
|
|
Exercice 4. ( 5 points) Sujet 47 On
dispose d’un dé équilibré à six faces et de deux urnes U et V contenant
des boules blanches ou rouges, indiscernables au toucher.
L’urne U contient 40 boules blanches et 60 boules rouges.
L’urne V contient 70 boules blanches et 30 boules rouges.
Un jeu consiste à lancer le dé puis tirer une boule dans l’une des
urnes. Si on obtient 1 ou 6 sur le dé, le tirage s’effectue dans l’urne
U. Si on obtient 2, 3, 4 ou 5 sur le dé, le tirage s’effectue dans
l’urne V.
On considère les événements :
𝑈 : « le tirage s’effectue dans l’urne U »
𝑉 : « le tirage s’effectue dans l’urne V »
𝐵 : « la boule tirée est blanche »
𝑅 : « la boule tirée est rouge ».
Sauf indication contraire, les probabilités seront arrondies au millième.
1. Représenter la situation à l’aide d’un arbre pondéré.
2. Déterminer la probabilité de l’évènement « la boule tirée est rouge ».
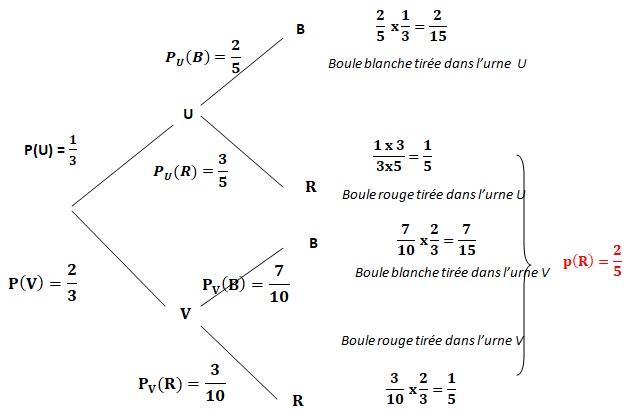
3. On tire une boule rouge. Quelle est la probabilité qu’elle ait été tirée dans l’urne U ?
PR(U)= P(R n U) / P(R) =1 /5 /(2 /5) = 0,5.
4. Pour jouer, il
faut miser 1 €. Le joueur gagne 3 € s’il tire une boule rouge et il ne
gagne rien s’il tire une boule blanche. On note 𝐺 la variable
aléatoire donnant le gain du joueur.
a. Déterminer la loi de probabilité de la variable aléatoire 𝐺.
On donnera le tableau de la loi de probabilité, mais aucune justification n'est demandée.
valeur de G
|
2
|
-1
|
probabilité
|
0,4
|
0,6
|
b. Calculer l’espérance mathématique de 𝐺. Interpréter ce résultat.
E =2 x0,4 -1 x0,6=0,2. En moyenne, on gagne 0,2 €.
|
Sujet 48.
Dans un aéroport, les portiques de sécurité servent à détecter les objets métalliques que peuvent emporter les voyageurs.
On choisit au hasard un voyageur franchissant un portique.
On note :
𝑆 l’événement « le voyageur fait sonner le portique » ;
𝑀 l’événement « le voyageur porte un objet métallique ».
On note 𝑆̅ et 𝑀̅ les événements contraires des événements 𝑆 et 𝑀.
On considère qu’un voyageur sur 500 porte sur lui un objet métallique.
On admet que :
Lorsqu’un voyageur franchit le portique avec un objet métallique, la probabilité que le portique sonne est égale à 0,95.
Lorsqu’un voyageur franchit le portique sans objet métallique, la probabilité que le portique ne sonne pas est de 0,96.
1. À l’aide des données de l’énoncé, préciser les valeurs de 𝑃(𝑀), 𝑃𝑀(𝑆) et 𝑃𝑀̅(𝑆̅).
P(M) =1 500 = 0,002. PM(S)=0,95. P nonM( non S) = 0,96.
2. Recopier et compléter l’arbre pondéré ci-dessous, modélisant cette situation :
3. Montrer que 𝑃(𝑆)= 0,04182.
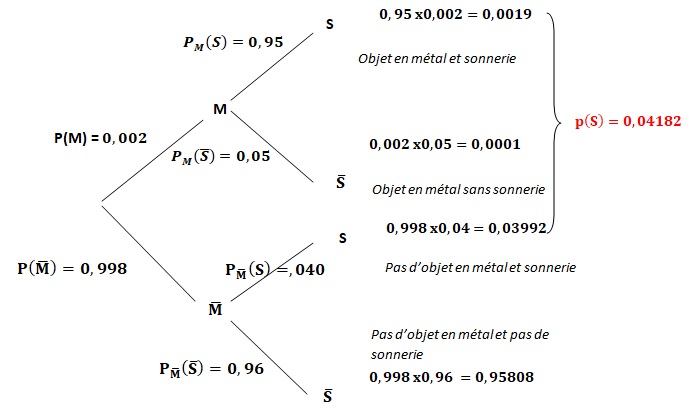
4. En déduire la
probabilité qu’un voyageur porte un objet métallique sachant qu’il a
fait sonner le portique en passant. On arrondira le résultat à 10−3.
PS(M) =P(S n M) / P(S)=0,0019 / 0,04182 =0,0454.
5. Les événements 𝑀 et 𝑆 sont-ils indépendants ?
P(M) x P(S) =0,002 x 0,04182 = 0,00008364, diffère de P(S n M)=0,0019.
Les événements M et S ne sont pas indépendants.
|
|