Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 51
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Dans un repère orthonormé, le cercle de centre A(2 ;-1) et de rayon 4 a comme équation :
a) (𝑥+2)2+(𝑦−1)2=16
b) (𝑥−2)2+(𝑦+1)2=4
c) (𝑥−2)2+(𝑦+1)2=16. Vrai.
d) (𝑥+2)2+(𝑦−1)2=4
2. Soit la droite (𝑑) d’équation cartésienne 2𝑥−𝑦+1 = 0.
Sachant que la droite (𝑑1) est perpendiculaire à la droite (𝑑), une équation de (𝑑1) peut être :
a) 𝑥−2𝑦+2 = 0
b) 𝑥+2𝑦−1 = 0. Vrai.
c) −2𝑥+𝑦−1 = 0
d) 𝑥−𝑦+2 = 0
3. L’expression de sin(𝜋−𝑥)+cos(𝑥+ 𝜋 / 2) est égale à :
a) −2sin(𝑥)
b) 0. Vrai.
c) 2sin(𝑥)
d) cos(𝑥)−sin (𝑥).
sin(𝜋−𝑥) = sin(x) ; cos(𝑥+ 𝜋 / 2) = - sin (x) ; sin(𝜋−𝑥)+cos(𝑥+ 𝜋 / 2) =0.
4. On considère la fonction polynôme du second degré 𝑓 définie sur ℝ par
𝑓(𝑥)= −3𝑥2+𝑥−5.
Le tableau de variations de cette fonction est :
f '(x) = -6x +1 ; f '(x)=0 si x = 1 /6.
f '(x) < 0 si x > 1 /6 et f(x) décroissante.
f '(x) > 0 si x < 1 /6 et f(x) croissante.
Réponse d.
5. À un jeu, la variable aléatoire donnant le gain algébrique 𝐺 suit la loi de probabilité suivante (en euros) :
valeurs de G
|
-25
|
-3
|
x
|
100
|
probabilité
|
1 /3
|
1 / 6
|
0,3
|
0,2
|
Sachant que l’espérance de 𝐺 est égale à 38 / 3 , la valeur de 𝑥 est :
a) 0 ; b) 5 ; c) 20 ; d) 25. Réponse b.
-25 / 3 -3 / 6+0,3x+0,2*100 =38 /3.
-25 / 3 -0,5+0,3x+20 =38 /3.
0,3x = 63 /3 -19,5 =(63- 58,5) /3 ; x = 4,5 /(3 *0,3) = 45 /9 = 5.
Sujet 52.
1. Pour tout entier naturel 𝑛, on définit la suite (𝑢𝑛) par : 𝑢𝑛=3×10𝑛/ 2𝑛+1.
La suite (𝑢𝑛) est une suite :
A. arithmétique de raison 3.
B. géométrique de raison 3.
C. arithmétique de raison 5.
D. géométrique de raison 5. Réponse D.
𝑢𝑛=3×(10 /2)𝑛/ 2 = 1,5 x 5n.
2. Dans un repère orthonormé du plan, on considère les points A(−2 ; 1) et B(2 ; 4).
La droite Δ passe par le point C(−1 ; 1) et admet le vecteur AB pour vecteur normal.
La droite Δ admet pour équation cartésienne :
A. 3𝑥−4𝑦+7=0.
B. 4𝑥+3𝑦+1=0.
C. 3𝑥−4𝑦−1=0.
D.4𝑥+3𝑦+7=0. Réponse B.
Coordonnées du vecteur AB (2-(-2) ; 4-1) soit (4 ; 3).
Equation cartésienne de cette droite : 4x+3y +d = 0.
C appartient à cette droite : 4*(-1) +3*1 +d = 0 ; d = 1.
3. Dans l’intervalle [0; 𝜋 /2], l’unique solution de l’équation : 2cos (𝑥+𝜋)+1=0 est :
A. 𝜋 / 3
B. −5𝜋 / 3.
C. 𝜋 / 6
D. 2𝜋 / 3. Réponse A.
cos (𝑥+𝜋) = -0,5 = cos (±2𝜋 / 3)
𝑥+𝜋 =±2𝜋 / 3 ; solution retenue x = 𝜋 -2𝜋 / 3 = 𝜋 / 3.
4. On considère la fonction 𝑓 définie et dérivable sur R par : 𝑓(𝑥)=e𝑥 / (1+e𝑥)
La fonction dérivée 𝑓′ de la fonction 𝑓 est définie par :
A. 𝑓′(𝑥)=e/ (1+e).
B. 𝑓′(𝑥)=e𝑥/ (1+e𝑥)2
C. 𝑓′(𝑥)=1
D. 𝑓′(𝑥)=−e𝑥/ (1+e𝑥)2. Réponse B.
On pose u = ex et v = 1+ex ; u' = ex ; v' = ex.
(u'v-v'u) / v2 = [e𝑥 (1+e𝑥)-ex ex] / (1+e𝑥)2= e𝑥/ (1+e𝑥)2.
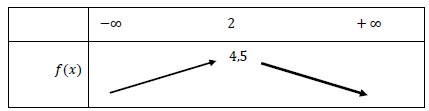
5. On considère la fonction 𝑓 définie sur R par : 𝑓(𝑥)=−0,5(𝑥+2)2+4,5.
On peut affirmer que :
A. Le tableau de variations de la fonction 𝑓 est donné ci-dessous :
B. La courbe représentative admet un sommet de coordonnées (4,5; −2).
C. Le signe de 𝑓(𝑥) est donné ci-dessous :

D. La fonction 𝑓 admet un minimum en −2 égal à 4,5.
f(x) = -0,5x2-2x+2,5 ; f '(x) = -x-2.
f '(x) < 0 si x > -2 et f(x) décroissante ; f '(x) > 0 si x < -2 et f(x) croissante ; f '(-2) = 0.
Axe de symétrie de la parabole : x = -(-2) / (2*(-0,5) = -2.
Racines de -0,5x2-2x+2,5 =0 ; discriminant D = (-2)2 -4*(-0,5)*2,5 = 9 =32.
x1 = (2+3) / (2*(-0,5)) =-5 et x2 = (2-3) / (2*(-0,5)) =1.
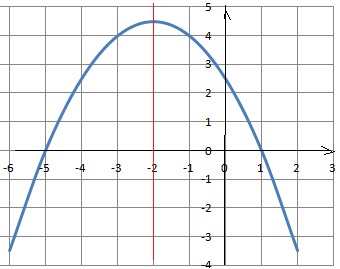 Réponse C. Réponse C.
|
|
Exercice 2. ( 5
points) Sujet 51. Une
note de musique est émise en pinçant la corde d’une guitare électrique.
La puissance du son émis, initialement de 120 watts, diminue en
fonction du temps écoulé après pincement de la corde.
Soit 𝑓 la fonction définie pour tout réel 𝑡 ≥0 par : 𝑓(𝑡)= 120 𝑒−0,14𝑡.
On admet que 𝑓(𝑡) modélise la puissance du son, exprimée en watt, à
l’instant 𝑡 où 𝑡 est le temps écoulé, exprimée en seconde, après
pincement de la corde.
On désigne par f ′ la fonction dérivée de 𝑓.
1. Calculer f ′(𝑡).
f '(t) = 120 *(-0,14)e-0,14t = -16,8 e-0,14t.
2. Dresser le tableau de variations de la fonction 𝑓 sur [0 ; +∞[ et interpréter ce résultat dans le contexte de l’exercice.
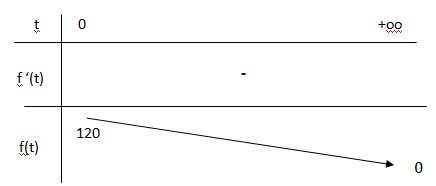
La puissance du son diminue avec le temps jusqu'à s'annuler.
3. Quelle sera la puissance du son, trois secondes après avoir pincé la corde ? Arrondir au dixième.
f(3) = 120 exp(-0,14*3)~78,8 watts.
4. On considère la fonction seuil ci-dessous :
def seuil():
t=0
puissance=120
while puissance>=60:
t=t+0.1
puissance=120*exp(-0.14*t)
return t
Que renvoie cette fonction seuil() ?
La fonction renvoie la durée au bout de laquelle la puissance du son est inférieure ou égale à 60 watts.
Sujet 52....
Une fleuriste met en vente quatre sortes de bouquets dont les tarifs et la composition sont indiqués ci-dessous :
Bouquet de tulipes orange : 10,50 €
Bouquet de roses orange : 23,50 €
Bouquet de tulipes blanches : 11,60 €
Bouquet de roses blanches : 25,50 €
- 72 % des bouquets mis en vente ne contiennent que des roses.
- Les autres bouquets mis en vente ne contiennent que des tulipes.
- 20 % des bouquets de tulipe mis en vente ne contiennent que des tulipes orange.
- 36 % des bouquets mis en vente ne contiennent que des roses blanches.
Un client achète au hasard un bouquet parmi ceux mis en vente par la fleuriste. On note :
- 𝑅 l’événement : « Le bouquet acheté par ce client est composé de roses. »
- 𝐵 l’événement : « Le bouquet acheté par ce client est composé de fleurs blanches. »
Les événements contraires des événements 𝑅 et 𝐵 sont notés respectivement 𝑅̅ et 𝐵̅.
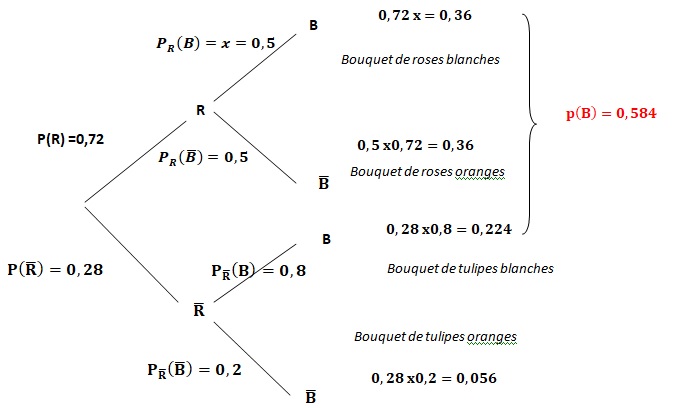
1. a. Donner, sans justifier, la probabilité 𝑃(𝑅∩𝐵).
Le bouquet est composé de roses blanches : 𝑃(𝑅∩𝐵) =0,72 x0,5=0,36.
b. Recopier et compléter le plus possible l’arbre de probabilité ci-dessous en traduisant uniquement les données de l’énoncé.
c. Montrer que 𝑃(𝐵)=0,584.
2. On note 𝑋 la variable aléatoire qui donne le prix d’un bouquet acheté par un client.
a. Recopier et compléter le tableau ci-dessous donnant, pour chaque valeur 𝑥𝑖 de 𝑋, la probabilité de l’événement {𝑋=𝑥𝑖}. Justifier.
xi
|
25,5
|
23,5
|
11,6
|
10,5
|
p(X=xi)
|
0,36
|
0,36
|
0,224
|
0,056
|
b. Calculer l’espérance de la variable aléatoire 𝑋. On arrondira le résultat au centième.
E(X) = 25,5 *0,36 +23,5 *0,36 +11,6 *0,224 +10,5*0,056 =9,18 +8,46 + 2,5984 +0,588 ~20,83 €.
|
|
Exercice 3. ( 5 points).
Sujet 51.
Un journal hebdomadaire est sur le point d’être créé.
Une étude de marché aboutit à deux estimations différentes concernant le nombre de journaux vendus :
1re estimation : 1 000 journaux vendus lors du lancement, puis une progression des ventes de 3 % chaque semaine.
2e estimation : 1 000 journaux vendus lors du lancement, puis une
progression régulière de 40 journaux supplémentaires vendus chaque
semaine.
On considère les suites (𝑢𝑛) et (𝑣𝑛) telles que, pour tout entier naturel 𝑛≥1, 𝑢𝑛 représente le nombre de journaux vendus la 𝑛-ième semaine selon la première estimation et 𝑣𝑛 représente le nombre de journaux vendus la 𝑛-ième semaine selon la deuxième estimation. Ainsi, 𝑢1=𝑣1=1 000.
1. On considère la feuille de calcul ci-dessous :
|
A
|
B
|
C
|
1
|
n
|
un
|
vn
|
2
|
1
|
1000
|
1000
|
3
|
2
|
1030
|
1040
|
4
|
3
|
1060,9
|
1080
|
5
|
4
|
1092,727
|
1120
|
Quelle formule, saisie en B3 et recopiée vers le bas, permet d’obtenir les termes de la suite (𝑢𝑛) ?
=B2*1,03
2.a. Donner la nature de la suite (𝑢𝑛) puis celle de la suite (𝑣𝑛). Justifier.
un+1 / un = 1,03, suite géométrique de raison 1,03.
vn+1-vn = 40, suite arithmétique de raison 40.
b. Montrer que pour tout entier naturel 𝑛≥1, 𝑣𝑛=960+40𝑛.
Initialisation : v1 =1000 = 960 +40 *1; v2 =1000 +40 =960 + 40*2. La propriété est vraie au rang 1.
Hérédité : 𝑣𝑛=960+40𝑛 est supposée vraie.
vn+1 = vn +40 = 960 +40(n+1). La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout n > 1.
c. Écrire, pour tout entier naturel 𝑛≥1, l’expression de 𝑢𝑛 en fonction de 𝑛.
un = 1000 * 1,03n-1.
3. On définit, pour tout entier 𝑛≥1, la suite (𝑤𝑛) par 𝑤𝑛=𝑣𝑛−𝑢𝑛. On donne ci-dessous un extrait de son tableau de valeurs :
n
|
1
|
2
|
|
19
|
20
|
21
|
22
|
wn
|
0
|
10
|
|
18
|
6
|
-6
|
-20
|
À partir de quelle semaine
le nombre de journaux vendus d’après la première estimation devient-il
supérieur au nombre de journaux vendus d’après la deuxième estimation ?
A partir de la 21è semaine.
Sujet 52.
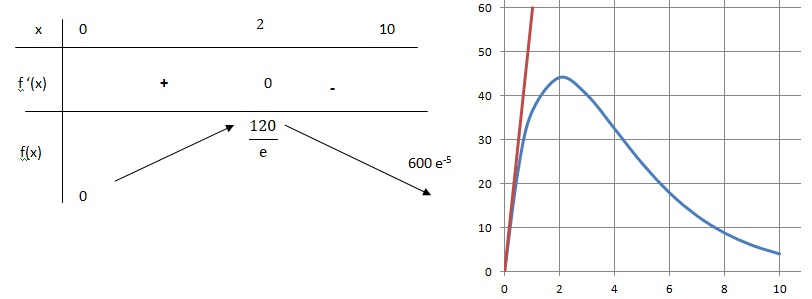
Soit 𝑓 la fonction définie sur l’intervalle [0;10] par : 𝑓(𝑥)=60𝑥e−0,5𝑥.
La fonction dérivée de la fonction 𝑓 est notée 𝑓′.
1. Démontrer que, pour tout réel 𝑥, 𝑓′(𝑥)=−30(𝑥−2)e−0,5𝑥.
On pose u = x et v = e-0,5x ; u' = 1 ; v' = -0,5e-0,5x ;
u'v +v'u = e-0,5x -0,5xe-0,5x =0,5(2- x)e-0,5x ; f '(x) =−30(𝑥−2)e−0,5𝑥.
2. Déterminer le signe de 𝑓′(𝑥) sur l’intervalle [0 ;10].
e−0,5𝑥 est positif ; le signe de f '(x) est celui de 2-x.
si x < 2, f '(x) > 0 ; si x >2, f '(x) < 0 ; si x = 2, f '(x) =0.
3. Établir le tableau de variation de la fonction 𝑓 sur l’intervalle [0 ;10].
On indiquera dans ce tableau les valeurs exactes des extremums.
4. Quelles sont les
coordonnées du point en lequel la tangente à la courbe représentative
de la fonction 𝑓 est parallèle à l’axe des abscisses ?
f '(2) =0. La tangente est parrallèle à l'axe des abscisses en x = 2.
5. Déterminer l’équation réduite de la tangente à la courbe représentative de la fonction 𝑓 au point d’abscisse 0.
Coefficient directeur de cette tangente : f '(0)=60.
Le point de coordonnée (0 ; 0) appartient à la tangente; équation réduite : y = 60x.
|
|
Exercice 4. ( 5 points) Sujet 51. On considère deux élevages de chatons sacrés de Birmanie :
Dans le premier élevage 75 % des chatons deviennent couleur Chocolat et 25 % deviennent couleur Blue.
Dans le second élevage 30 % des chatons deviennent couleur Chocolat et 70 % deviennent couleur Blue.
Une animalerie se fournit dans ces deux élevages. Elle achète 40 % de ses chatons au premier élevage et 60 % au deuxième.
On choisit au hasard un chaton de l’animalerie.
On note 𝐴 l’événement « Le chaton provient du premier élevage » et 𝐵 l’événement « Le chaton est de couleur Blue ».
On note 𝐴̅ l’événement contraire de 𝐴 et 𝐵̅ l’événement contraire de 𝐵.
1. a. Recopier sur la copie et compléter l’arbre de probabilité ci-dessous :
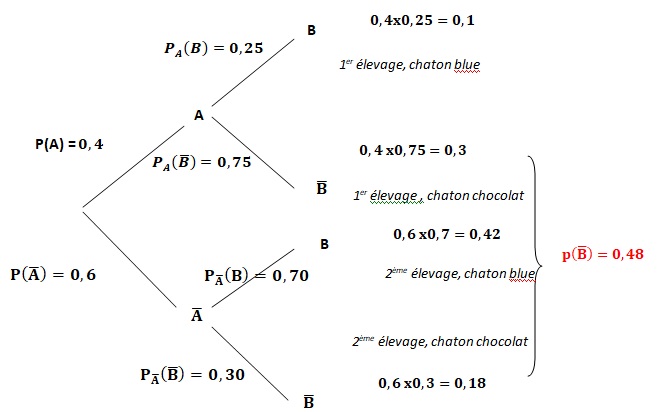
b. Calculer 𝑃(𝐴̅∩𝐵̅) et interpréter ce résultat.
0,30 x0,6 =0,18.
La probabilité qu'un chaton soit issu du second élevage et devienne chocolat est de 0,18.
c. Montrer que la probabilité que le chaton soit de couleur Chocolat est 0,48.
Formule des probabilité totale : 0,3 +0,18 = 0,48.
d. Sachant que Jules a choisi un chaton couleur Blue dans cette
animalerie, quelle est la probabilité que le chaton provienne du
deuxième élevage ? On donnera le résultat à 10−2 près.
PB(non A) = P(N n non A) / P(B) =0,18 / 0,48 = 3 / 8 =0,375 ~0,38.
2. Le responsable du rayon fixe à 100 € le prix de vente d’un chaton couleur Blue et à 75 € le prix d’un chaton couleur Chocolat.
On choisit au hasard un chaton de l'animalerie et on désigne par 𝑋 la
variable aléatoire égale au prix en euros du chaton acheté. Déterminer
la loi de probabilité de 𝑋.
valeur de X
|
100
|
75
|
probabilité
|
0,52
|
0,48
|
.
|
Sujet 52.
Le
1er janvier 2019, le propriétaire d’un appartement a fixé à 650 euros
le montant des loyers mensuels pour l’année 2019. Chaque 1er janvier,
le propriétaire augmente de 1,52 % le loyer mensuel.
On modélise l’évolution du montant des loyers mensuels par une suite (𝑢𝑛). L’arrondi à l’unité du terme 𝑢𝑛 représente le montant, en euros, du loyer mensuel fixé le 1er janvier de l’année (2019+𝑛), pour 𝑛 entier naturel. Ainsi 𝑢0=650 euros.
1. a. Calculer le montant du loyer mensuel fixé le 1er janvier 2020.
u1 = 650 x1, 0152~660 €
b. Quelle est la nature de la suite (𝑢𝑛) ? Préciser sa raison et son premier terme.
Suite géométrique de raison 1,0152 et de premier terme 650.
c. Calculer le montant du loyer mensuel qui, selon ce modèle, sera fixé pour l’année 2027.
n =8 ; u8 = 650 x1,01528~733 €.
2. Pour calculer la
somme totale des loyers perçus par le propriétaire durant les années
2019 à 2019+A, on utilise la fonction ci-dessous, écrite en langage
Python.
1 def somme(A):
2 S=0
3 n=0
4 while n<=A:
5 S=S+7800*1.0152**n
6 n = n + 1
7 return S
L’exécution de ce programme pour quelques valeurs de A donne les résultats ci-dessous :
somme(0)=7800 : somme(1) =15718 ; somme(2) =23757 ; somme(3) =31918 ; somme(8) =74623.
a. Interpréter, dans le contexte de l’exercice, le résultat obtenu lors de l’appel somme(1).
somme(1) représente le total des loyers annuels des années 2019 et 2020.
b. Déterminer la
somme totale des loyers perçus par le propriétaire durant les années
2022 à 2027 incluses. On arrondira le résultat à l’unité.
somme(8)-somme(2) =74 623-23 757=50 866 €.
|
|