Nombres
complexes, classe de première technologique.
.
.
|
|
1.a. Compléter les colonnes 3 à 4 du tableau suivant :
Nombre complexe z.
|
Affixe
|
Partie réelle
|
Partie imaginaire
|
Nombre complexe conjugué
|
2-3i
|
A
|
2
|
-3i
|
2+3i
|
-3+4i
|
B
|
-3
|
4i
|
-3-4i
|
2i
|
C
|
0
|
2i
|
-2i
|
1.b.Placer dans le plan complexe les points A, B, C d'affixe z.
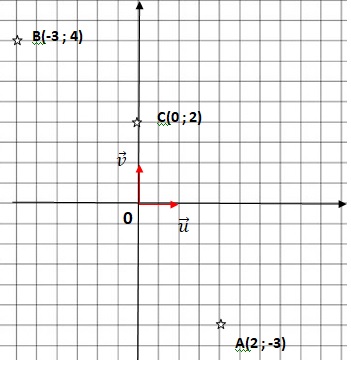
1.c. Calculer le module de chaque nombre complexe.
z = 2-3i.
|z| = racine carrée [(22 +(-3)2] =racine carrée (4+9) = racine carrée (13) soit 13½.
z = -3+4i.
|z| = racine carrée [(42 +(-3)2] =racine carrée (16+9) = racine carrée (25) soit 5.
z = 2i.
|z| = racine carrée [(22 ] =racine carrée (4) = 2.
1.d. Calculer les distances AB, AC et BC.
AB = |zB-zA|.
zB-zA = -3 +4i -(2-3i) = -3 +4i-2+3i = -5 +7i.
|zB-zA| = racine carrée ((-5)2 +72)=racine carrée (25+49)=racine carrée (74) soit AB=74½.
AC = |zC-zA|.
zC-zA = 2i -(2-3i) = 2i-2+3i = -2 +5i.
|zC-zA| = racine carrée ((-2)2 +52)=racine carrée (4+25)=racine carrée (29) soit AC=29½.
BC = |zC-zB|.
zC-zB = 2i -(-3+4i) = 2i+3-4i = 3 -2i.
|zC-zB| = racine carrée ((-2)2 +32)=racine carrée (4+9)=racine carrée (13) soit BC=13½.
|
2. On considère le nombre complexe z = 3 [cos (p/3) + i sin ( p/3)].
2.a. Placer dans le plan complexe le point M d'affixe z.
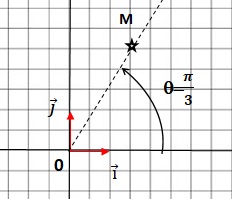
2.b. Quels sont le module et l'argument de z ?
Module de z : 3.
Argument de z : p / 3.
2.c. Déterminer l'écriture algébrique de z.
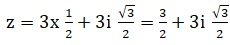
3. On considère le nombre complexe z = 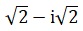 soit z = 2½-i 2½. soit z = 2½-i 2½.
3.a. Placer dans le plan complexe le point M d'affixe z.
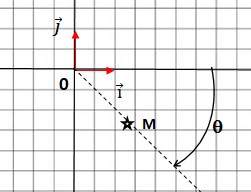
3.b. Quels sont le module et l'argument de z ?
Module :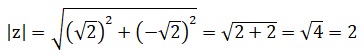
Argument : 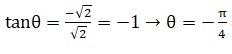
3.c. Déterminer la forme trigonométrique de z.
z = 2 [ cos(-p/4) +i sin (-p/4)].
ou bien : z = 2 [ cos(p/4) -i sin (p/4)].
|
4. Ecrire sous forme algébrique les nombes complexes suivants :
a. 2 x(-1+3i) -2i x (4-2i).
-2 +6i -8i +4i2 = -2-2i+4x(-1) = -2-2i-4 = -6-2i.
b. (2-3i)(5-4i).
10-8i-15i +12i2 =10-23i+12x(-1) =10-23i-12 =-2-23i.
c. (2-3i)2 =4 +(3i)2 -12i = 4 +9 i2 -12i =4+9x(-1)-12i = -5-12i.
d. 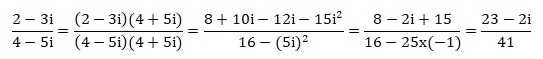
|
|