Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 57
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Dans un repère orthonormé, on considère la parabole P d’équation 𝑦 = 2𝑥2 + 4𝑥 − 11, de sommet S et d’axe de symétrie la droite D . Quelle est la bonne proposition ?
A. S(−4 ; 5) et D a pour équation 𝑦 = 5.
B. S(−1 ; −17) et D a pour équation 𝑥 = −1.
C. S(−1 ; −13) et D a pour équation 𝑥 = −1. Vrai.
D. S(−1 ; −13) et D a pour équation 𝑦 = −1.
Equation de la droite D : x= -b / (2a) = -4 /(2*2)= -1.
Coordonnées du sommet : (-1; f(-1)= -13).
2. Une
expérience aléatoire met en jeu des événements 𝐴 et 𝐵 et leurs
événements contraires non 𝐴 et non 𝐵. L’arbre pondéré ci-dessous
traduit certaines données de cette expérience aléatoire.
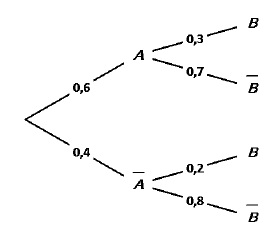
On a alors :
A. 𝑃(𝐵) = 0,5. ( 0,3 *0,6 +0,4*0,2 =0,18+0,08=0,26).
B. 𝑃(𝐴 ∩ 𝐵) = 0,9. ( 0,6 *0,3)=0,18)
C. 𝑃𝐴(𝐵) = 0,18. (P(A n B) / P(A) =0,18 /0,6 =0,3)
D. 𝑃𝐵(𝐴) = 9 / 13. (P(A n B) / P(B) =0,18 /0,26 =18 /26 =9 /13). Vrai.
3. On considère le nombre réel 𝑎 =18𝜋 / 5.
Un des nombres réels suivants a le même point image que le nombre réel 𝑎 sur le cercle trigonométrique. Lequel ?
A. 3𝜋 / 5.
B. 63𝜋 / 5
C. −12𝜋 / 5. Vrai.
D. −3𝜋 / 5.
18𝜋 / 5 = 10𝜋 / 5 + 8𝜋 / 5 =2𝜋 + 8𝜋 / 5.
18𝜋 / 5 = 20𝜋 / 5 - 2𝜋 / 5 =4𝜋 - 2𝜋 / 5.
63𝜋 / 5 = 60𝜋 / 5 + 3𝜋 / 5 = 12𝜋 + 3𝜋 / 5.
−12𝜋 / 5 = −10𝜋 / 5 -2𝜋 / 5 =-2𝜋 - 2𝜋 / 5.
4. On considère la fonction 𝑓 définie sur𝐑 par 𝑓(𝑥)= 𝑥e𝑥.
La fonction dérivée de la fonction 𝑓 est notée 𝑓′. On a alors :
A. 𝑓′(𝑥)=e𝑥.
B. 𝑓′(𝑥)=(1+𝑥)e𝑥. Vrai.
C. 𝑓′(𝑥)=𝑥e𝑥.
D. 𝑓′(𝑥)=2𝑥e𝑥.
On pose u =x et v = ex ; u' = 1 ; v' = ex ; u'v+v'u =ex+xex=(1+x=ex.
5.Parmi les relations suivantes, quelle est celle qui permet de définir une suite géométrique de terme général 𝑢𝑛 ?
A. 𝑢𝑛=𝑢𝑛−1 / 2. Vrai.
B. 𝑢𝑛=𝑢𝑛−1 + 2.
C. 𝑢𝑛=2𝑢2𝑛−1.
D. 𝑢𝑛=2𝑢𝑛−1+10.
Sujet 58.
1. Pour tout réel 𝑥, e2𝑥 + e4𝑥 est égal à :
a) e6𝑥 ; b) e2𝑥 (1 + e2) ; c) e3𝑥 (e𝑥 + e−𝑥 ) vrai ; d) exp(8𝑥2).
e3x *e-x+e3x*ex =e3𝑥 (e-x + e𝑥 )
2. Dans
le plan muni d'un repère orthonormé, on considère les vecteurs 𝑢⃗⃗(−5;
2) et 𝑣⃗(4; 10) et la droite (d) d'équation : 5𝑥 + 2𝑦 + 3 = 0.
a) 𝑢⃗⃗ et 𝑣⃗ sont colinéaires
b) 𝑢⃗⃗ est un vecteur normal à la droite (d)
c) ) 𝑢⃗⃗ et 𝑣⃗ sont orthogonaux. Vrai ( le produit scalaire de ces vecteurs vaut : -5*4+2*10=0 )
d) 𝑢⃗⃗ est un vecteur directeur de (d).
3. La dérivée 𝑓′ de la fonction 𝑓 définie sur R par 𝑓(𝑥) = (2𝑥 − 1)e−𝑥 est :
a) 2𝑥e−𝑥 ; b) −2𝑥e−𝑥 ; c) (−2𝑥 + 3)e−𝑥 vrai ; d) 2e−𝑥 + (2𝑥 − 1) e−𝑥.
On pose u = 2x-1 et v = e-x ; u' = 2 ; v' = -e-x ; u'v +v'u=2e-x-(2x-1)e-x =(−2𝑥 + 3)e−𝑥 .
4. Pour tout réel 𝑥, on a sin(π + 𝑥) =
a) −sin (𝑥) vrai ; b) cos (𝑥) ; c) sin (𝑥) ; d) −cos (𝑥)
5. Soit 𝑓 une fonction définie et dérivable sur R dont la courbe représentative est donnée.
La tangente à la courbe au point 𝐴 est la droite 𝑇.
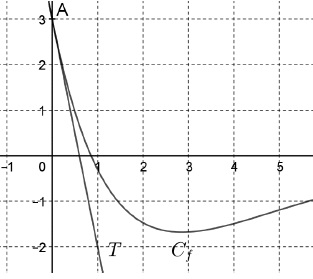
a) 𝑓′(0) = 3 ; b) 𝑓′(0) = 1 / 5 ; c) 𝑓′(0) = 5 ; d) 𝑓′(0) = −5. Vrai.
f '(0) = coefficient directeur de la tangente en A = -5.
|
|
Exercice 2. ( 5
points) Sujet 57. On considère la fonction 𝑓 définie sur 𝐑 par 𝑓(𝑥)=𝑥3+3𝑥²+3𝑥−63.
On appelle C sa courbe représentative dans un repère orthonormé.
1. Déterminer 𝑓′(𝑥).
f '(x) = 3x2+6x+3 = 3(x+1)2.
2. Etudier le signe de 𝑓′(𝑥) sur 𝐑.
(x+1)2 > 0; f '(x) >0 et f '(-1) =0.
3. Etablir le tableau de variations de la fonction 𝑓 sur 𝐑.
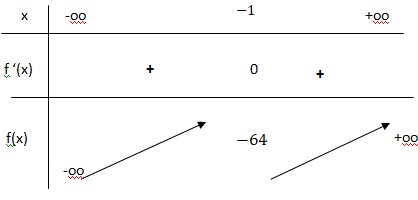
4. Justifier que la tangente à la courbe C au point d’abscisse −1 est la droite D d’équation 𝑦=−64.
Coefficient directeur de cette tangente : f '(-1) =0.
La tangente passe par le point de coordonnées (-1 ; f(-1) = -64.
Equation de cette tangente : y = -64.
5. Déterminer en quels points de la courbe C la tangente à la courbe est parallèle à la droite d’équation 𝑦 =3𝑥−100.
Coefficient directeur de ces tangentes : 3 = f '(x) ; 3(x+1)2 = 3 ; (x+1)2 =1 ; x+1 = ±1 soit x = 0 et x = -2.
f(0) = -63 ; f(-2) = -65.
Coordonnées de ces points ( 0 ; -63) et (-2 ; -65).
Sujet 58.
La population d’une ville A augmente chaque année de 2%. La ville A avait 4600 habitants en 2010.
La population d’une ville B augmente de 110 habitants par année. La ville B avait 5100 habitants en 2010.
Pour tout entier 𝑛, on note 𝑢𝑛 le nombre d’habitants de la ville A et 𝑣𝑛 le nombre d’habitants de la ville B à la fin de l’année 2010 + 𝑛.
1. Calculer le nombre d’habitants de la ville A et le nombre d’habitants de la ville B à la fin de l’année 2011.
u1 =4600 x1,02 =4692.
v1 = 5100 +110 = 5210.
2. Quelle est la nature des suites (𝑢𝑛) et (𝑣𝑛) ?
(un) : suite géométrique de raison 1,02 ; (vn) suite arithmétique de raison 110.
3. Donner l'expression de 𝑢𝑛 en fonction de 𝑛, pour tout entier naturel 𝑛 et calculer le nombre d’habitants de la ville A en 2020.
un = 4600 *1,02n ; u10=4600*1,0210 ~5607.
4. Donner l'expression de 𝑣𝑛 en fonction de 𝑛, pour tout entier naturel 𝑛 et calculer le nombre d’habitants de la ville B en 2020.
vn =5100+110n ; v10=5100+1100=6200.
5. Reproduire et
compléter sur la copie l'algorithme ci-dessous qui permet de déterminer
au bout de combien d’années la population de la ville A dépasse celle
de la ville B.
def année ():
u=4600
v=5100
n=0
while u < = v :
u=u*1,02
v=v+110
n=n+1
return n
|
|
Exercice 3. ( 5 points).
Sujet 57.
Pour
placer un capital de 5 000 euros, une banque propose un placement à
taux fixe de 5 % par an. Avec ce placement, le capital augmente de 5 %
chaque année par rapport à l’année précédente. Pour bénéficier de ce
taux avantageux, il ne faut effectuer aucun retrait d’argent durant les
quinze premières années. On modélise l’évolution du capital disponible
par une suite (𝑢𝑛). On note 𝑢𝑛 le capital disponible après 𝑛 années de placement. On dépose 5 000 euros le 1er janvier 2020. Ainsi 𝑢0=5 000.
1. Montrer que 𝑢2=5512,5. Interpréter ce résultat dans le contexte de l’exercice.
u1 = 5000 *1,05=5250 ; u2 = 5250 *1,05=5512,5.
Le premier janvier 2022, le placement est égal à 5512,5 €.
2. Exprimer 𝑢𝑛+1 en fonction de 𝑢𝑛.
un+1=1,05 un.
3. Quelle est la nature de la suite (𝑢𝑛) ? Préciser son premier terme et sa raison.
Suite géométrique de raison 1,05 et de premier terme 5000.
4. Exprimer 𝑢𝑛 en fonction de 𝑛.
un = 5000 *1,05n.
5. Justifier que le capital aura doublé après 15 années de placement.
u15=5000 *1,0515 ~10 395 €.
Sujet 58.
Soit ℎ la fonction définie sur [0 ; 26] par :
ℎ(𝑥) = −𝑥3 + 30𝑥2 − 108𝑥 − 490.
1. Soit ℎ′ la fonction dérivée de ℎ. Exprimer ℎ′(𝑥) en fonction de 𝑥.
h'(x)=-3x2+60x-108.
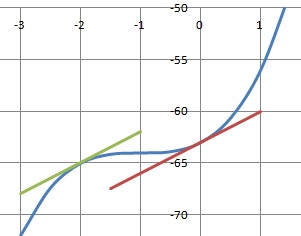
2. On note 𝐶 la courbe représentative de ℎ et 𝐶′ celle de ℎ′.
a. Identifier 𝐶 et 𝐶′ sur le graphique orthogonal ci-dessous parmi les trois courbes 𝐶1, 𝐶2 et 𝐶3 proposées.
b. Justifier le choix pour 𝐶′.
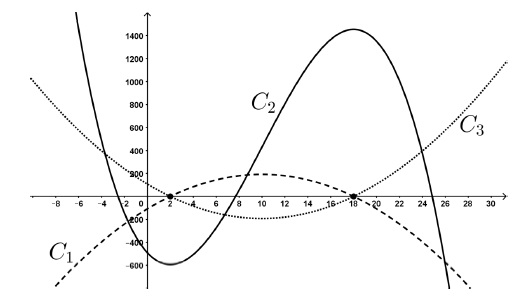
h(0) = -490, courbe C2.
h(x) est décroissante sur ]-oo ; 2]; h'(x) est négative, courbe C1.
3. Soit (T) la tangente à 𝐶 au point 𝐴 d'abscisse 0. Déterminer son équation réduite.
Coefficient directeur de T : h'(0) = -108.
Le point de coordonnées 0 ; -490) appartient à T.
Equation réduite de T : y = -108x-490.
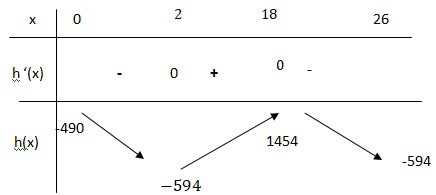
4. Étudier le signe de ℎ′(𝑥) puis dresser le tableau de variation de la fonction ℎ sur [0; 30].
Solutions de -3x2+60x-108 =0 soit x2-20x+36=0.
Discriminant D =(-20)2-4*36=256=162.
x1 = (20-16)/2=2 ; x2=(20+16)/2=18.
h'(x) est positive sur [2 ; 18] ; h'(x) est négative sur ]-oo; 2] et [18 ; +oo[.
h'(2) = h'(18) =0.
|
|
Exercice 4. ( 5 points) Sujet 57. Dans
un repère orthonormé du plan, on considère les points A(−2 ;1), B(1 ;2)
et E(0 ;−5). On appelle C le cercle de centre A passant par B.
1. Justifier qu’une équation du cercle C est (𝑥+2)²+(𝑦−1)²=10.
Rayon du cercle R2 = AB2 =(1-(-2))2 +(2-1)2 = 10
Equation du cercle de centre A(-2 ; 1) : (𝑥+2)²+(𝑦−1)²=10.
2. Calculer le produit scalaire suivant :
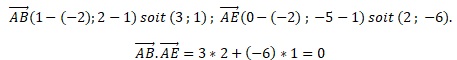
3. Que peut-on en déduire pour les droites (AB) et (AE) ?
Les droites (AB) et (AE) sont perpendiculaires.
4. Déterminer une équation cartésienne de la droite (AE).
Coordonnées d'un vecteur normal à la droite (AE) : (3 ; 1).
Equation cartésienne de cette droite : 3x+y+c=0.
E(0 ; -5) appartient à cette droite : -5+c=0 soit c = 5.
3x+y+5=0.
5. Calculer les coordonnées des points d’intersection de (AE) et du cercle C.
y =-3x-5.
(x+2)2 +(-3x-5-1)2= 10.
x2+4x+4 +9x2+36+36x=10.
10x2+40x+30=0 ; x2+4x+3=0
Discriminant D =42-4*3=4=22.
Solutions : x1 = (-4+2)/2 =-1 et x2 = (-4-2) / 2 = -3.
y1 =-2 et y2 =4.
Les points d’intersection de (AE) et du cercle C ont pour coordonnées :(-1 ; -2) et (-3 ; 4).
|
Sujet 58.
Une
entreprise qui fabrique des aiguilles dispose de deux sites de
production, le site A et le site B. Le site A produit les trois-quarts
des aiguilles, le site B l’autre quart. Certaines aiguilles
peuvent présenter un défaut. Une étude de contrôle de qualité a révélé que :
2% des aiguilles du site A sont défectueuses ;
4% des aiguilles du site B sont défectueuses.
Les aiguilles provenant des deux sites sont mélangées et vendues ensemble par lots.
On choisit une aiguille au hasard dans un lot et on considère les événements suivants :
𝐴 : l’aiguille provient du site A ;
𝐵 : l’aiguille provient du site B ;
𝐷 : l’aiguille présente un défaut.
1. D’après les données de l’énoncé, donner la valeur de la probabilité de l’événement 𝐴 que l’on notera 𝑃(𝐴).
p(A) = 0,75.
2. Recopier et compléter sur la copie l'arbre de probabilités ci-dessous en indiquant les probabilités sur les branches.
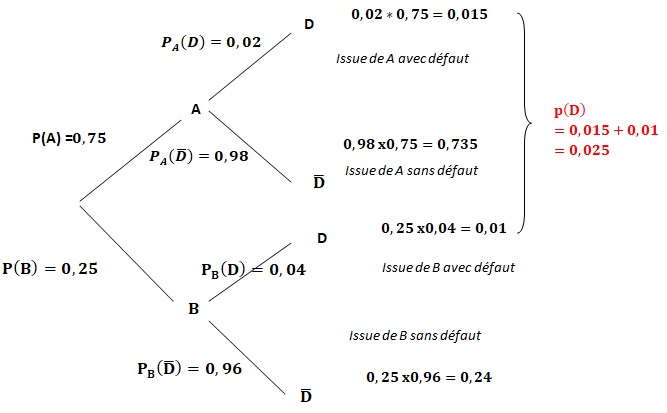
3. Quelle est la probabilité que l’aiguille ait un défaut et provienne du site A ?
0,02 *0,75=0,015.
4. Montrer que 𝑃(𝐷) = 0,025.
5. Après inspection, l’aiguille choisie se révèle défectueuse. Quelle est la probabilité qu’elle ait été produite sur le site A ?
PD(A) = P(D n A) / P(D)=0,015 /0,025=0,60.
|
|