Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 59
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Soit la suite arithmétique (𝑢𝑛) de premier terme 𝑢0 = 2 et de raison 0,9. On a :
a) 𝑢50=47. Vrai.
b) 𝑢50=100,9
c) 𝑢50=−47
d) 𝑢50=−100,9.
u50 = u0 +50 *0,9 =2+45=47.
2. Soit la suite géométrique ( 𝑣𝑛) de premier terme 𝑣0= 2 et de raison 0,9.
La somme des 37 premiers termes de la suite ( 𝑣𝑛) est :
a) 2x(1-0,938) / (1-0,9).
b) 2x(1-0,937) / (1-0,9). Vrai.
c ) 0,9x(1-238) / (1-2).
d) 0,9x(1-237) / (1-2).
3. Un programme en langage Python qui retourne la somme des entiers de 1 à 100 est :
a) def Somme()
s=0
while s <100 :
s=s+1
returne (s)
|
b) def Somme()
s=0
while s <100 :
s=2*s+1
returne (s) |
c) def Somme()
s=0
for kin range(101):
s=s+k
returne (s) |
d) def Somme()
s=0
for kin range(100):
s=s+k
returne (s) |
Réponse c.
4. On a 𝑥∈[−𝜋 / 2 ; 0] et cos 𝑥=0,8 alors :
a) sin𝑥=0,6
b) sin𝑥=−0,6. Vrai.
c) sin𝑥=−0,2
d) sin𝑥=0,2.
sin2(x) = 1-0,82 = 0,36 ; sin (x) = ±0,6.
𝑥∈[−𝜋 / 2 ; 0], alors sin(x) < 0.
5. Le nombre réel 13𝜋 /4 est associé au même point du cercle trigonométrique que le réel :
a) −14 𝜋 / 4
b) −3 𝜋 /4. Vrai.
c) 7 𝜋 / 4
d) 19 𝜋 / 4.
13𝜋 /4 =16𝜋 /4 -3𝜋 /4=4𝜋 -3𝜋 /4
Sujet 60.
1.
Dans le repère orthogonal suivant on a tracé quatre courbes, chacune
associée à une fonction de variable réelle 𝑥 et d'expression 𝑒𝜆𝑥 où 𝜆 est un paramètre réel. Quelle courbe possède le plus petit paramètre 𝜆 ?
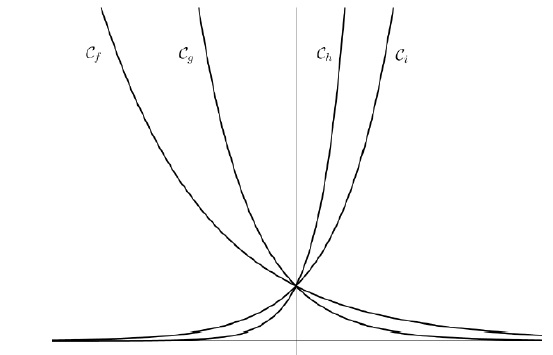
l est négatif pour les fonctions f et g, positif pour les fonctions h et i.
Choisissons une abscisse négative : le point correspondant de la courbe Cg a une ordonnée supérieure à celle du point de la courbe Cf.
Réponse b, courbe Cg.
2. On
choisit au hasard un couple ayant deux enfants et on note 𝑋 la
variable aléatoire égale au nombre de filles du couple. On admet que la
probabilité qu’un enfant soit une fille est égale à 0,5 et qu’il y a
indépendance du sexe de l’enfant entre deux naissances.
Déterminer 𝑃(𝑋 ≥1).
Valeur de X
|
0 ( deux garçons)
|
1 ( une fille et un garçon)
|
2 ( deux filles.
|
P(X)
|
0,5 *0,5 = 0,25
|
0,5
|
0,5 *0,5 = 0,25
|
P(X> 1)= 0 0,5 +0,25 = 0,75. Réponse d.
3. On a représenté ci-dessous la courbe 𝒞 de la fonction sinus dans un repère orthogonal.

A0, A1, A2, A3 et A4 sont des points de 𝒞 et ils ont tous la même ordonnée.
Parmi les segments suivants, lequel a pour longueur la période de la fonction sinus ?
a) [A0 ; A1]
b) [A0 ; A2]
c) [A0 ; A3]. Vrai.
d) [A0 ; A4]
4. Soit la fonction 𝑓 définie sur ℝ par 𝑓(𝑥)=0,5𝑥2−2𝑥+1.
On considère l’équation 𝑓(𝑥)=0, d’inconnue 𝑥∈ℝ. L’ensemble des solutions de cette équation est :
a) ∅
b) {2−√2 ; 2+√2}
c) {2−√6 ; 2+√6}
d) {4−2√2 ; 4+2√2}.
Discriminant D = (-2)2 -4*0,5*1=2.
Solutions x= (2±2½) / (2*0,5) = 2±2½. Réponse b.
5. 𝐴𝐵𝐶 est un triangle tel que : 𝐴𝐵=5, 𝐵𝐶=2, angle (𝐴𝐵𝐶̂)=60. La longueur 𝐴𝐶 est égale à :
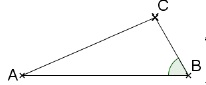
a) 19½ vrai ; b) 21½ ; c) 28½ ; d) 29½.
AC2 =BC2 + AB2 -2*AB*BC cos 60 = 22 +52 -2*2*5 cos 60 =29-20 *0,5 = 19.
|
|
Exercice 2. ( 5
points) Sujet 59. Le
dépistage d’une maladie particulière que l’on appelle M s'effectue par
un test basé sur le dosage d’une hormone particulière. D’après une
étude, cette maladie M touche 1,5 % de la population.
Si une personne est atteinte par la maladie M, le test sera positif
dans 95 % des cas ; alors que si la personne n’est pas atteinte par la
maladie M, le test sera négatif dans 99 % des cas.
On soumet à ce test une personne prise au hasard dans la population.
On note :
● A l’évènement « La personne est atteinte par la maladie M.» ;
● T l’évènement « Le test est positif.».
1. Déterminer la probabilité pour que le test soit positif et que la personne choisie ne soit pas malade.
2. Déterminer la probabilité pour que le test soit positif.
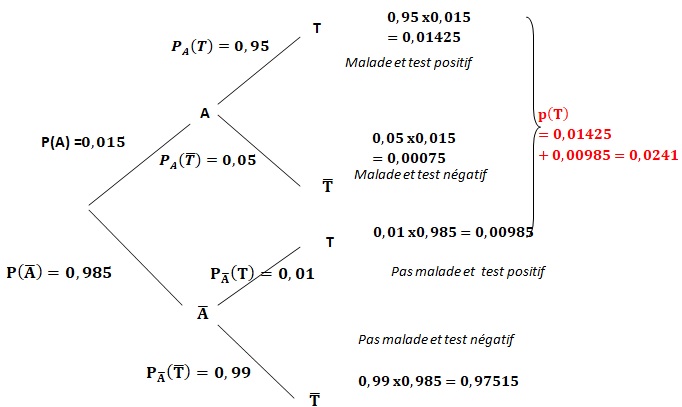
3. Calculer 𝑃T (A̅) (Arrondir à 10 – 3 près). Interpréter ce résultat dans le contexte de l’exercice.
𝑃T (A̅) = P(T n non A) / P(T) =0,00985 / 0,0241 ~0,409.
Parmi 1000 tests positifs, 409 personnes ne sont pas malades.
Sujet 60.
On modélise la diffusion dans le sang d’un médicament de 1 gramme par intraveineuse (fonction 𝑓1, courbe représentative 𝒞1) ou par voie orale (fonction 𝑓2, courbe représentative 𝒞2) pendant une durée de 10 heures. Plus précisément :
𝑓1(𝑡) modélise la proportion du médicament dans le sang
à l’instant 𝑡, où 𝑡 est le temps en heure après injection par
intraveineuse ;
𝑓2(𝑡) modélise la proportion du médicament dans le sang
à l’instant 𝑡, où 𝑡 est le temps en heure après administration par
voie orale.
Pour tout réel 𝑡 de l’intervalle [0 ;10], on admet que 𝑓1(𝑡)=e−0,57𝑡 et 𝑓2(𝑡)=1,75 𝑡 e−𝑡.
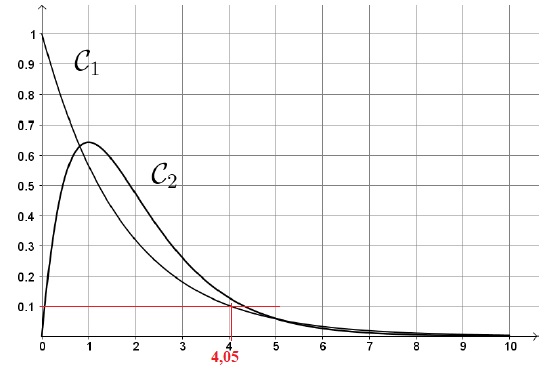
Les courbes 𝒞1 et 𝒞2 de 𝑓1 et 𝑓2 sont représentées ci-dessous.
1. Injection par voie intraveineuse
a. Déterminer le sens de variation de la fonction 𝑓1.
f1 est strictement décroissante.
b. Résoudre graphiquement 𝑓1(𝑡)<0,1. Interpréter la réponse dans le contexte.
t appartient à [4,05 ; 10].
Au delà de 4 heures après la prise, la concentration en médicament dans le sang est inférieure à 0,1 g.
2. Administration par voie orale
On note 𝑓2′ la fonction dérivée de la fonction 𝑓.
a. Montrer que, pour tout 𝑡 de [0 ; 1], 𝑓2′(𝑡)=1,75(1−𝑡)e−𝑡.
On pose u = 1,75 t et v = e-t ; u' = 1,75 ; v' = -e-t.
u'v+v'u = 1,75e-t -1,75te-t = 1,75(1−𝑡)e−𝑡.
b. Construire le tableau de variations de la fonction 𝑓2.
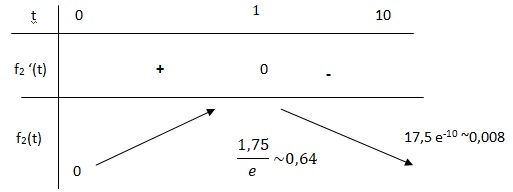
c. À quel instant 𝑡 la proportion de médicament dans le sang est-elle la plus élevée ?
Une heure après la prise, la concentration du médicament est la plus élevée.
|
|
Exercice 3. ( 5 points).
Sujet 59.
Soit 𝑓 la fonction définie sur ℝ par 𝑓(𝑥)=(𝑥2−2,5𝑥+1) 𝑒𝑥.
1. On note 𝑓′ la fonction dérivée de 𝑓.
a) Montrer que, pour tout réel 𝑥, 𝑓′(𝑥)=(𝑥2−0,5𝑥−1,5) 𝑒𝑥.
On pose u = x2-2,5x+1 et v = ex ; u' = 2x-2,5 ; v' = ex ;
u'v+v'u=(2x-2,5)ex +( x2-2,5x+1)ex =(𝑥2−0,5𝑥−1,5) 𝑒𝑥.
b) Étudier les variations de 𝑓 sur ℝ.
ex étant toujours positif, le signe de f '(x) est celui de 𝑥2−0,5𝑥−1,5.
Solutions de 𝑥2−0,5𝑥−1,5=0. Déterminant D =(-0,5)2 +4*1,5=6,25 =2,52.
x1 = (0,5 +2,5) / 2 =1,5 ; x2 = (0,5 -2,5) / 2 =-1.
f '(x) est négatif si x appartient à [-1 ; 1,5] ; f(x) est décroissante
f '(x) est positif si x appartient à ]-oo ; -1 } union [1,5 ; +oo[. f(x) est croissante
f '(-1) = f '(1,5) = 0. f admet deux extrémum.
2. On note 𝒞𝑓 la courbe représentative dans un repère et 𝒯 la tangente à 𝒞𝑓 de la fonction 𝑓 au point A d’abscisse 0.
a) Déterminer une équation de la tangente 𝒯.
Coefficient directeur de cette tangente = f '(0)= -1,5.
A (0 ; 1) appartient à cette tangente : 1 = 0+b ; b = 1.
Equation de la tangente : y = -1,5x+1.
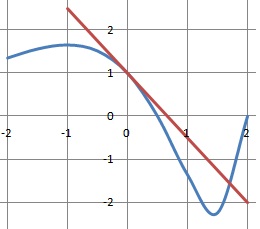
b) On admet que la tangente 𝒯 recoupe la courbe 𝒞𝑓 au point P d’abscisse 𝑎 strictement positive. A l’aide de votre calculatrice, donner un encadrement de 𝑎 au dixième près.
la calculatrice donne a ~1,8.
Sujet 60.
Dans un pays, le nombre de créations d’entreprise augmente 1,5% par mois.
En janvier 2018 on compte 50 000 créations d’entreprise.
On modélise le nombre de créations d’entreprise au 𝑛-ième mois par une suite (𝑢𝑛) telle que 𝑢𝑛+1=𝑢𝑛×1,015 et 𝑢0=50, 𝑢𝑛 est exprimé en milliers d’entreprises.
1.a. Calculer 𝑢1.
u1 =50 x1,015=50,75 milliers.
b. Interpréter ce résultat dans le contexte de l’exercice.
En février 2018 on compte 50 750 créations d’entreprise.
2.a. Quelle est la nature de la suite (𝑢𝑛) ?
Suite géométrique de raison 1,015 et de premier terme 50.
b. Exprimer 𝑢𝑛 en fonction de 𝑛.
un = 50 * 1,015n.
c. Un journaliste
annonce qu’au total dans l’année 2018, près de 652 000 entreprises se
sont créées. Donner un calcul permettant de justifier les propos du
journaliste.
Somme des 12 premiers termes de cette suite géométrique : 50 (1-1,01512) / (1-1,015) =652 milliers.
|
|
Exercice 4. ( 5 points) Sujet 59. Le
centre commercial « L’autre faubourg » de Cholet a été conçu en forme
circulaire de 110 m de rayon permettant une visibilité à 360° et une
accessibilité optimale, notamment aux personnes à mobilité réduite. Le
parking, situé à l’intérieur du disque, dessert l’ensemble des 32
magasins.
On munit le plan d’un repère orthonormé de centre O. L’unité est le mètre.
Les entrées des magasins du centre commercial sont situées sur le cercle 𝒞 de centre O et de rayon 110.
1) Une allée
centrale couverte a été construite afin de permettre aux automobilistes
de rejoindre les magasins en cas d’intempéries. Elle est modélisée par
la droite (AD) avec A(−30;15) et D(80;−40).
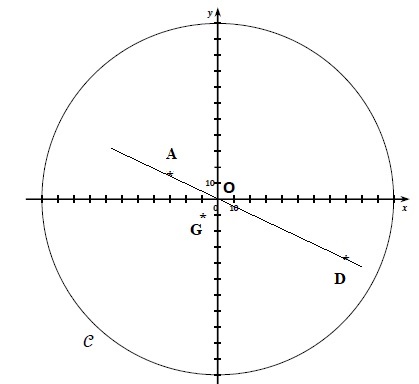
a) Déterminer une équation du cercle 𝒞.
x2+y2 = 1102=12100.
b) Démontrer que le point O appartient à la droite (AD).
2) Camille qui vient de garer sa voiture en G(−10;−10) sous une pluie
battante, souhaite se mettre à l’abri sous cette allée centrale, le
plus rapidement possible.
a) Calculer le produit scalaire suivant.
b) Le point de la droite (AD) le plus proche de G est-il O ?

O n'est pas le projeté orthogonal de G sur la droite (AD). Le point de la droite (AD) le plus proche de G n'et pas le point O.
|
Sujet 60.
(𝑂 ; 𝑖⃗ ; 𝑗⃗) est un repère orthonormé du plan.
On considère les points 𝐴, 𝐵 et 𝐶 de coordonnées respectives (−2 ;0), (6 ;0) et (0 ;6).
Les points 𝐴′, 𝐵′ et 𝐶′ milieux respectifs des segments [𝐵𝐶], [𝐴𝐶] et [𝐴𝐵].
Le cercle Γ passant par les points 𝐴′, 𝐵′ et C’ a pour centre le point 𝐼 de coordonnées (1 ;2).
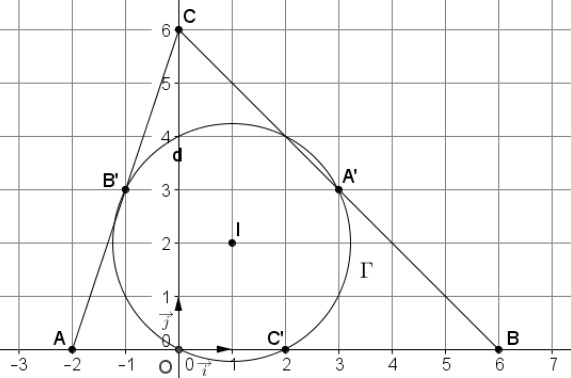
1.
a. Calculer le rayon de ce cercle.
IC'2 =(2-1)2 +(0-2)2 =5 ; IC = 5½.
b. En déduire qu’une équation du cercle Γ est (𝑥−1)2+(𝑦−2)2=5.
(x-xI)2 +(y-yI)2 = rayon2.
(𝑥−1)2+(𝑦−2)2=5.
2. Propriété des hauteurs du triangle 𝐴𝐵𝐶
a. On admet que 𝑂 est le pied de la hauteur issue de 𝐶. Montrer que le point 𝑂 est sur le cercle Γ.
(𝑥O−1)2+(𝑦O−2)2=5.
(-1)2 +(-2)2 = 5. Donc O appartient au cercle.
b. Soit 𝐻𝐴 le pied de la hauteur issue de 𝐴. Montrer que 𝐻𝐴 a pour coordonnées (2 ;4).
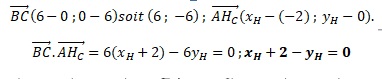
Equation réduite de la droite BC : y= -x+c.
B(6 ; 0) appartient à cette droite :0= -6+c ; c = 6.
y= -x+6.
HC appartient à cette droite : yH= -xH+6.
xH +2-(-xH+6)=0 ; 2 xH -4=0 ; xH = 2. Par suite yH =4.
c. Justifier que le point 𝐻𝐴 est sur le cercle Γ.
(𝑥H−1)2+(𝑦H−2)2= (2−1)2+(4−2)2=5.
Le point 𝐻𝐴 est sur le cercle Γ.
|
|