Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 61
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. La courbe ci-contre Cf est
la représentation graphique, dans un repère orthonormé, d’une fonction
f. Les droites d et d’ sont respectivement les tangentes à la courbe Cf aux points d’abscisses 1 et 2.
Les équations réduites de d et d’ sont respectivement :
d : 𝑦=2𝑥−2 et d’ : 𝑦=−𝑥+2.
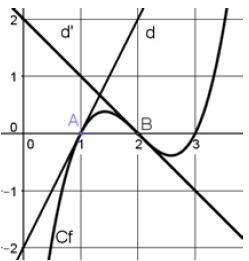
Parmi les propositions suivantes, laquelle est juste ?
a) f '(1)=0.
b) f '(2)=2
c) f '(2)=-1. Vrai.
d) f '(1) =-2.
f '(1) est le coefficient directeur de la droite d et f '(2) celui de la droite d'.
2.Soit 𝑥 ∈ [𝜋 /2 ; 3𝜋 /2] tel que sin𝑥= 0,5 .
Parmi les propositions suivantes, laquelle est juste ?
a) cos x = -3½ /2. Vrai.
b) cos x = 3½ /2.
c ) x=𝜋 /6.
d) x= -𝜋 /6.
𝑥 ∈ [𝜋 /2 ; 3𝜋 /2], alors cos x < 0.
cos2 x = 1-sin2x = 1-0,52 = 0,75 = 3 /4 ; cos x = -3½ /2.
3. Soit (O, I, J) un repère orthonormé du plan.
Soit A et B deux points de coordonnées respectives (3 ; 4) et (4 ; 0).
Parmi les propositions suivantes, laquelle est juste ?

4. Soit (O, I, J) un repère orthonormé du plan.
Soit d une droite dont une équation cartésienne est : 3𝑥+2𝑦−10=0 .
Une équation cartésienne de la droite d’ perpendiculaire à la droite d et passant par le point A de coordonnées (1 ; 2) est :
A : 3𝑥+2𝑦−7=0
B : 2𝑥+3𝑦−8=0
C : 2𝑥−3𝑦+4=0. Vrai.
D : 3𝑥−2𝑦+1=0.
Equation de la droite perpendiculaire : 2x-3y+c=0.
A(1 ; 2) appartient à la droite perpendiculaire.
2-3*2+c=0 ; c = 4.
5. Soit (O, I, J) un repère orthonormé du plan.
Soit A et B deux points de coordonnées respectives (1 ; 2) et (5 ; -2).
Une équation cartésienne du cercle C de diamètre [AB] est :
A : 𝑥2+𝑦2−8𝑥−2𝑦+7=0
B : (𝑥−1)2+(𝑦−2)2=32
C : 𝑥2+𝑦2−4𝑥+2𝑦−5=0
D : 𝑥2+𝑦2−6𝑥+1=0. Vrai.
Coordonnées du centre du cercle : (xA+xB) / 2 ; (yA+yB) / 2 soit ( 3 ; 0).
AB2 =(5-1)2+(-2-2)2= 16+16=32=(2R)2 ; R2 = 8.
Equation du cercle : (x-3)2 +y2 =8 ; x2-6x+9+y2=8.
Sujet 62.
1.
Soit 𝑐 un nombre réel strictement supérieur à 1. Sur l’ensemble des
nombres réels, la fonction polynôme 𝑓 définie par 𝑓(𝑥)=𝑥2+2𝑥+𝑐.
a. change de signe exactement 2 fois
b. change de signe exactement une fois
c. est toujours positive. Vrai.
d. est toujours négative.
f '(x) = 2x+2 = 2(x+1).; f '(x) = 0 pour x = -1.
Ordonnée du minimum : f(-1) = 1-2+c =c-1, positif.
La parabole ne coupe pas l'axe des abscisses. f(x) > 0.
2. Si 𝑥 est un nombre réel appartenant à l’intervalle [ − 𝜋 ; 0] tel que cos𝑥 = 3 / 5, alors sin𝑥 a pour valeur.
a) 0,8 ; b) -0,8 ; c) -0,4 ; d) on ne peut pas savoir.
Sur l’intervalle [ − 𝜋 ; 0] , sin x est négatif ou nul
sin2x = 1-cos2x = 1-0,62 =0,64 ; sin x = -0,8. Réponse b.
3. Le quadrilatère 𝐴𝐵𝐶𝐷 est un carré. On a :
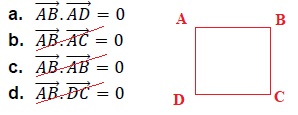
4. La droite d’équation 2𝑥−𝑦+1=0 coupe l’axe des abscisses au point 𝐴 de coordonnées :
a. 𝐴(0 ;1)
b. 𝐴(0,5 ;0)
c. 𝐴(0 ;− 1)
d. 𝐴(− 0,5 ;0). Vrai.
yA =0 ; 2xA-0+1=0 ; xA = -0,5.
5. Pour tout réel 𝑥, 𝑒𝑥 / e−𝑥 est égal à
a. – 1
b. e−2𝑥
c. (e𝑥)2. Vrai.
d. e0.
ex *ex = e2x = (e𝑥)2.
|
|
Exercice 2. ( 5
points) Sujet 61. Une balle en caoutchouc est lâchée sans vitesse initiale d’une hauteur de 2 mètres au-dessus du sol.
Le choc n’étant pas parfaitement élastique, la balle rebondit jusqu’à
une hauteur de 1,60 mètre et continue à rebondir, en atteignant après
chaque rebond une hauteur égale au 4 / 5 de la hauteur du rebond
précédent.
On modélise les hauteurs atteintes par la balle par une suite (ℎ𝑛) où pour tout entier naturel 𝑛, ℎ𝑛 est la hauteur, exprimée en mètres, atteinte par la balle au 𝑛-ième rebond. On a alors ℎ0= 2.
1. a. Donner ℎ1 et ℎ2 .
h1 =2 x4 /5 =1,6 ; h2 =1,6 x4 /5 =1,28.
b. Pour tout entier naturel 𝑛, exprimer ℎ𝑛+1 en fonction de ℎ𝑛.
hn+1=4 /5 hn =0,8 hn.
c. En déduire la nature de la suite (ℎ𝑛). On précisera sa raison et son premier terme.
Suite géométrique de premier terme 2 et de raison 0,8.
d. Déterminer le sens de variation de la suite (ℎ𝑛).
La raison étant comprise entre ]0 ; 1[ et u0 > 0, la suite est décroissante.
2. Déterminer le
nombre minimal 𝑁 de rebonds à partir duquel la hauteur atteinte par la
balle est inférieure à 20 cm. Expliquer la démarche employée.
hn = 2 *0,8n < 0,2 ; h10 = 2 *0,810 ~0,215 m = 21,5 cm.
h11 = 2 *0,811 ~0,172 m = 17,2 cm. N = 11 rebonds.
Sujet 62.
Un
biologiste étudie une population de bactéries dans un milieu fermé. À
l’instant initial, il y a 10 000 bactéries et la population augmente de
15% par heure.
On modélise la situation par une suite (𝑢𝑛) pour laquelle, pour tout entier naturel 𝑛, 𝑢𝑛 représente une estimation du nombre de bactéries au bout de 𝑛 heures.
On a donc 𝑢0= 10 000.
1. Expliquer pourquoi la suite (𝑢𝑛) vérifie pour tout entier naturel 𝑛 :
𝑢𝑛=10 000 × 1,15𝑛.
2. Quelle est la nature de la suite (𝑢𝑛). On précisera le premier terme et la raison.
Il s'agit d'une suite géométrique de raison 1 +15 /100 = 1,15 et de premier terme 10 000.
3. Combien y aura-t-il de bactéries au bout de 10 heures ?
u10 = 10 000 *1,1510 ~40 456.
4. On considère la fonction suivante définie en langage Python.
def bacteries(N) :
u=10000
for i in range(N) :
u=u*1.15
return u
On a appelé cette fonction en donnant différentes valeurs au paramètre 𝑛 et l’on a dressé le tableau suivant.
n
|
10
|
100
|
1000
|
10 000
|
bactéries (n)
|
40 455
|
1,2 1010
|
4,99 1064 |
3,052 10307 |
Quelle interprétation peut-on donner de ces résultats dans le contexte de l’exercice ?
Le nombre de bactéries semble tendre vers m'infini quand le nombre d'heures devient très grand.
5. Lorsque la
population atteint 200 000 bactéries, le biologiste répand un
désinfectant afin de tester son efficacité. Une heure plus tard, il
reste 4 000 bactéries. Quel est le pourcentage de diminution du nombre
de bactéries?
(200 000 -4000) / 200 000 = 0,98 (98 %).
|
|
Exercice 3. ( 5 points).
Sujet 61.
Un
restaurant propose à sa carte deux types de dessert : un assortiment de
macarons et une part de tarte tatin. Des études statistiques montrent
que :
l’assortiment de macarons est choisi par 50 % des clients ;
la part de tarte tatin, est choisie par 30 % des clients ;
20 % des clients ne prennent pas de dessert ;
aucun client ne prend plusieurs desserts.
Le restaurateur a remarqué que :
parmi les clients ayant pris un assortiment de macarons, 80 % prennent un café ;
parmi les clients ayant pris une part de tarte tatin, 60 % prennent un café ;
parmi les clients n’ayant pas pris de dessert, 90 % prennent un café.
On interroge au hasard un client de ce restaurant.
On note les événements suivants :
M : « Le client prend un assortiment de macarons » ;
T : « Le client prend une part de tarte tatin » ;
P : « Le client ne prend pas de dessert » ;
C : « Le client prend un café » et C̅ l’événement contraire de C.
1. En utilisant les données de l’énoncé, préciser la valeur de 𝑃(T) probabilité de T et celle de 𝑃T(C) probabilité de l’évènement C sachant que T est réalisé.
p(T) =0,3 ; 𝑃T(C)= 0,6.
2. Recopier et compléter l’arbre ci-dessous :
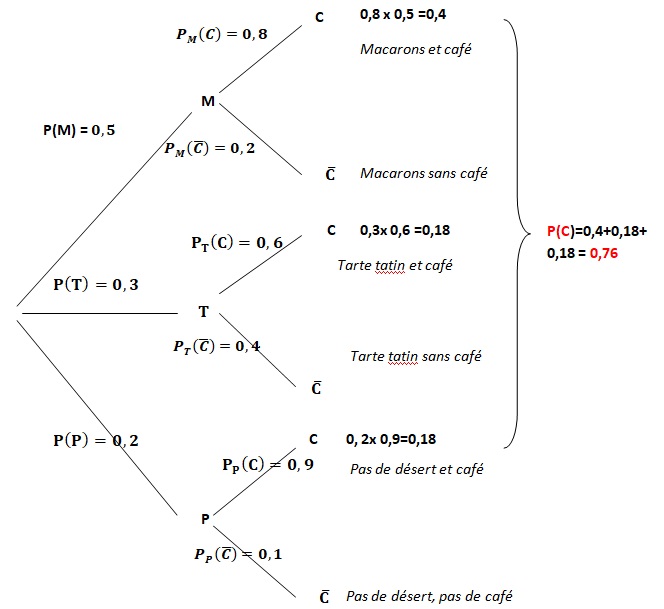
3. a. Exprimer par une phrase ce que représente l’évènement M∩C puis calculer 𝑃(M∩C).
Le client prend des macarons et un café. 𝑃(M∩C) = 0,8 *0,5 = 0,4.
b. Montrer que 𝑃(C)=0,76.
4. Quelle est la
probabilité que le client prenne un assortiment de macarons sachant
qu’il prend un café? (On donnera le résultat arrondi au centième).
PC(M) =𝑃(M∩C) / P(C) =0,4 / 0,76 ~053.
Sujet 62.
Claire
joue régulièrement à un jeu de simulation de tournois de judo en ligne.
Les adversaires qu’elle combat sont générés automatiquement de manière
aléatoire selon le niveau atteint dans le jeu.
Elle a atteint le niveau le plus élevé, celui de la ceinture noire. Les
scores relevés par le jeu montrent qu’elle gagne dans 45% des cas si
son adversaire est ceinture noire et dans 70% si son adversaire n’est
pas ceinture noire.
Claire commence un tournoi et un premier adversaire est généré par le
jeu. A ce niveau la probabilité d’affronter un adversaire ayant une
ceinture noire est 0,6.
On note :
- N l’événement : « l’adversaire est ceinture noire » ;
- G l’événement : « Claire gagne le combat ».
1. Recopier et compléter l’arbre pondéré ci-dessous modélisant cette situation.
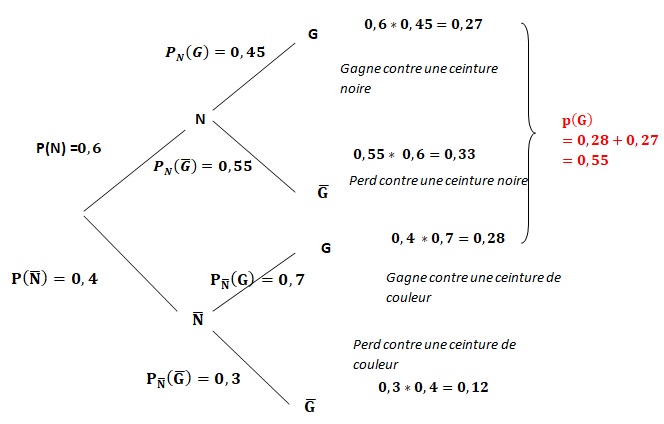
2. Calculer la probabilité que l’adversaire soit ceinture noire et que Claire gagne son tournoi.
0,6 * 0,45=0,27.
3. Montrer que la probabilité que Claire gagne son combat est 0,55.
0,28 +0,27 = 0,55.
4. Claire vient de perdre un combat. Quelle est la probabilité que le combat ait été contre une ceinture noire ?
Probabilité de perdre le combat : 1-0,55 = 0,45.
Probabilité de perdre contre une ceinture noire : 0,33 / 0,45 =33 / 45 =11 / 15.
5. On considère dans cette question que la probabilité que Claire gagne est 0,55. Elle fait deux combats successifs.
On note 𝑋 la variable qui compte le nombre de victoires. Donner la loi de probabilité de 𝑋.
Nombre de combats gagnés
|
2
|
1
|
0
|
Probabilité
|
0,55 *0,55 =0,3025
|
1-(0,3025+0,2025)=0,495
|
0,45*0,45=0,2025
|
.
|
|
Exercice 4. ( 5 points) Sujet 61. Une entreprise vend des smartphones d’un seul modèle « haut de gamme ».
Le service marketing modélise le nombre de smartphones modèle « haut de
gamme » vendus par trimestre en fonction du prix de vente 𝑥 par la
fonction 𝑁 définie par
𝑁(𝑥)= 100e−2𝑥 où :
𝑥 est le prix de vente en milliers d’euros d’un smartphone modèle «
haut de gamme ». Le prix du smartphone modèle « haut de gamme » est
compris entre 400€ et 2000€ ; on a donc 𝑥∈[0,4 ; 2].
𝑁(𝑥) est le nombre de smartphones modèle « haut de gamme » vendus trimestriellement en millions d’unités.
1. Si le service
commercial fixe le prix de vente de ce smartphone modèle « haut de
gamme » à 1000 €, quel sera le nombre de smartphones vendus
trimestriellement ? On arrondira le résultat à mille unités.
N(1)=100 *e-2=13,534.
La recette trimestrielle 𝑅(𝑥) est obtenue en multipliant le nombre de
smartphones modèle « haut de gamme » vendus par le prix de vente. On
obtient 𝑅(𝑥)=𝑥×𝑁(𝑥) en milliards d’euros.
Le coût de production en milliards d’euros en fonction du nombre de
smartphones modèle « haut de gamme » fabriqués est modélisé par la
fonction 𝐶 définie par 𝐶(𝑥) = 0,4 ×𝑁(𝑥) où 𝑥 est le prix de vente
en milliers d’euros.
Le bénéfice est obtenu en calculant la différence entre la recette et le coût de production.
2. Vérifier que le bénéfice trimestriel peut être estimé à 8,120 milliards d’euros pour un prix de vente 1000 €.
R(1) =13,534. C(1)=0,4*13,534 =5,413. Bénéfice trimestriel : 13,534 - 5,413 =8,121.
3. Montrer que le
bénéfice trimestriel s’exprime en milliards d’euros en fonction du prix
de vente 𝑥 en milliers d’euros par : 𝐵(𝑥)=(100𝑥 – 40) e−2𝑥 .
R(x) = x N(x) ; C(x) = 0,4 N(x) ; B(x) =x N(x) -0,4 * N(x) =(x-0,4)N(x) = (x-0,4 )*100e-2x = (100𝑥 – 40) e−2𝑥 .
4. On admet que pour tout réel 𝑥∈[0,4 ; 2],𝐵′(𝑥)=(180−200𝑥 )e−2𝑥.
Étudier les variations de la fonction 𝐵 sur l’intervalle [0,4 ; 2].
e-2x étant positif, le signe de B'(x) est celui de 180-200x.
B'(x) = 0 pour x = 0,9.
Si x < 0,9, B'(x) >0 et B(x) est croissante.
Si x > 0,9, B'(x) < 0 et B(x) est décroissante.
Si x = 0,9, le bénéfice est maximum.
5. À quel prix faut-il vendre ces smartphones pour assurer un bénéfice maximal ?
Le bénéfice est maximum pour un prix de vente de 900 €.
|
Sujet 62.
On
modélise la valeur de vente (en milliers d’euros) d’une voiture
électrique en fonction du nombre 𝑥 d’années à partir de sa mise sur le
marché par la fonction 𝑓 définie sur l’intervalle [0 ; 10] par
𝑓(𝑥)=35e−0,22𝑥.
1. Calculer 𝑓(0). Quel est le prix de vente de cette voiture au moment de la mise sur le marché ?
f(0)= 35 milliers d'euros.
2. Donner une valeur approchée du prix de vente au bout de 5 ans et 6 mois.
f(5,5)=35 e-0,22 *5,5 ~10,44 milliers d'euros.
3. On admet que la fonction 𝑓 est dérivable et on note 𝑓’ sa fonction dérivée. Montrer que pour tout 𝑥 appartenant à [0 ; 10],
𝑓′(𝑥)=− 7,7e−0,22𝑥.
f '(x) = 35 *(-0,22) e-0,22x=− 7,7e−0,22𝑥.
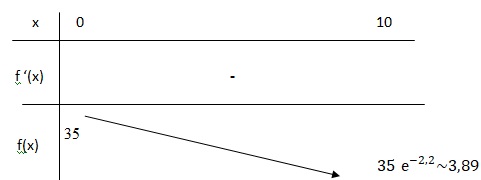
4. Dresser le tableau de variation de la fonction 𝑓.
e-0,22x étant positif, f '(x) est toujours négative et f(x) est strictement décroissante.
5. Un client
souhaite revendre sa voiture dès que celle-ci aura un prix de vente
inférieur à 10 000 euros. Après combien de mois après avoir acheté sa
voiture pourra-t-il la revendre ?
35 e-0,22x < 10 ; e-0,22x < 10 /35 ; -0,22 x < ln(10/35) ; -0,22x < -1,253 ; x > 1,253 / 0,22 ; x ~5,7 ans soit 5 ans et 9 mois.
|
|