Physique
chimie, un ballon pour les compétitions internationales de football,
réalisation d'une végétation métallique.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Un ballon
pour les compétitions internationales de fottball.
L’objectif de cet exercice est d’étudier le gonflage d’un ballon et son
utilisation dans des lieux de compétitions d’altitude différente. Nous
nous intéresserons ainsi à deux lois liées à cette situation : la loi
de Mariotte, qui permet d’étudier le gonflage et la loi de statique des
fluides qui permet de réfléchir à l’influence de l’altitude sur le
gonflage.
1. Étude expérimentale et
utilisation de la loi de Mariotte.
Une expérience est menée au laboratoire pour tester la loi de Mariotte
à l’aide d’un microcontrôleur et d’un capteur de pression.
On suit le protocole expérimental suivant :
- remplir initialement une seringue avec 30 cm3 d’air ;
- relier la seringue au capteur de pression connecté à un
microcontrôleur ;
- téléverser le programme « Mesure Pression » présenté ci-dessous dans
le microcontrôleur ;
- faire varier le volume du gaz dans la seringue et noter alors la
valeur de la pression correspondante affichée sur l’écran LCD relié au
microcontrôleur.
1.1. Adaptation du
programme « Mesure Pression »
Un extrait du programme associé au pilotage du microcontrôleur dans le
montage expérimental précédent est donné ci-dessous.
1.1.2. Dans le
programme, la valeur de la pression est affichée sans décimale.
Expliquer comment modifier la ligne 39 du programme pour que la valeur
de la pression soit affichée avec 2 décimales.
1.1.3. Expliquer
comment modifier la ligne 43 pour que les mesures soient faites toutes
les 3 secondes.

1.2. Traitement de
mesures obtenues en faisant varier le volume du gaz.
Pour chaque volume d’air choisi dans la seringue, le microcontrôleur
indique des valeurs de pression toutes les 2 secondes. Ces valeurs sont
très proches, mais fluctuent légèrement. Le tableau ci-dessous
rassemble les valeurs de la pression P affichée par l’écran LCD du
microcontrôleur pour différents volumes du gaz dans la seringue :
V
(cm3)
|
20
|
25
|
30
|
35
|
40
|
50
|
P(hPa)
|
1505
|
1195
|
998
|
852
|
745
|
600
|
P
V ( hPa cm3)
|
3,01
104
|
2,9875
104
|
2,994
104
|
2,982
104
|
2,98
104
|
3
104
|
1.2.1. Énoncer la loi de Mariotte.
Pour une masse de gaz constante prise à température constante, le
produit de la pression par le volume du gaz est constant.
1.2.2. Exploiter
ces mesures pour tester la loi de Mariotte. On explicitera précisément
la méthode utilisée.
Le produit P V ( 3ème ligne du tableau) est pratiquement constant.
Plus grand écart entre les valeurs extrèmes ( 3,01 -2,98) 104
=3 102 (0,01 soit 1 %).
La loi de Mariotte est vérifiée.
1.3. Gonflage d’un
ballon de football
On utilise un gonfleur électronique de ballon ayant les
caractéristiques suivantes :
- débit d’air à l’entrée du gonfleur : 4 litres par minute ;
- arrêt automatique quand la pression souhaitée est atteinte.
On souhaite gonfler, à l’aide de ce gonfleur, un ballon de football de
compétition de diamètre égal à 22 cm pour obtenir une pression de l’air
à l’intérieur du ballon de 2,1 105 Pa. On admet qu’avant le
gonflage le ballon est totalement dégonflé et que le volume d’air à
l’intérieur est négligeable. On admet également que la température
reste constante pendant le gonflage. On précise que l’air entrant dans
le compresseur est à la pression atmosphérique.
1.3.1. On appelle V0
le volume d’air à prélever dans le milieu extérieur pour le gonflage, V1
et P1 le volume d’air et la pression à l’intérieur du ballon
une fois qu’il est gonflé.
Montrer que V0=P1×V1 / P0.
Initialement, l'air occupe le volume V0 et sa pression est P0.
Dans le ballon gonflé, l'air occupe le volume V1 et sa
pression est P1.
La masse d'air est constante ; la température est constante.
La loi de Mariotte s'écrit : P1×V1
= P0 V0 soit V0=P1×V1
/ P0.
1.3.2. Montrer que la durée
nécessaire au gonflage, à l’aide du gonfleur électronique, est voisine
de 3 minutes.
V1 =4 / 3 p
r3 =4 / 3 x3,14 x1,13 = 5,57 dm3 =
5,57 litres.
V0 = 2,1 x 5,57 / 1,0 = 11,7 litres.
Durée (s) = V0(litres) / débit ( litre / min) =11,7 / 4 ~ 3
minutes.
|
|
2. Utilisation du ballon dans des
lieux de compétitions d’altitudes différentes.
On s’intéresse dans cette partie à la loi fondamentale de la statique
des fluides pour modéliser l’évolution de la pression atmosphérique en
fonction de l’altitude. Cette loi précise que, pour un fluide au repos
incompressible de masse volumique r, la différence de pression
entre
deux points, A et B, s’exprime par la relation :
PB−PA=ρ×g ×( zA−zB)
Dans cette relation :
- la masse volumique r
s’exprime en kg m-3 ;
- l’intensité de pesanteur g s’exprime en N kg-1 ;
- les altitudes zA et zB s’expriment en m et sont
repérées sur un axe vertical ascendant Oz.
Les villes de Denver et de New York se sont portées candidates pour
accueillir les matchs de la coupe du monde de football 2026 organisée
conjointement par les États-Unis, le Canada et le Mexique.
2.1. Comparer
qualitativement la valeur de la pression au point A à celle au point B.
zA < zB conduit à PB−PA
< 0 soit PA > PB.
2.2. Évaluer la
différence de pression atmosphérique PNY−PD entre
les villes de New York située à 10 mètres d’altitude et de Denver
située à 1600 mètres d’altitude. Pour les deux villes, on suppose que
la masse volumique de l’air a pour valeur r
= 1,1 kg m-3 et et que l’intensité
de
la pesanteur a pour valeur g = 9,8 N kg-1.
PNY−PD =1,1 x9,8 (1600-10)= 1,7 104 Pa.
2.3. Sur le site
Planet-Terre de l’École Normale Supérieure de Lyon, différents modèles
de l’atmosphère sont proposés.
· Modèle 1 : la masse volumique de l'air dépend de la pression et de la
température. On suppose que la température varie selon une fonction
affine décroissante de l’altitude.
· Modèle 2 : la masse volumique de l'air est constante, quelle que soit
l'altitude.
Les graphes correspondants à chacun des deux modèles, et représentant
l’évolution de la pression atmosphérique en fonction de l’altitude,
sont donnés ci-dessous (par souci d’échelle l’axe vertical n’est pas
gradué à partir de l’origine).
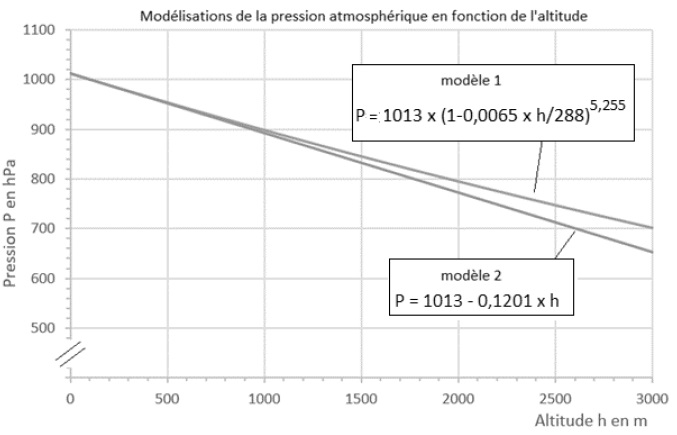
On considère que ces deux modèles sont équivalents quand les valeurs de
pression qu’ils donnent diffèrent entre elles de moins de 5 %.
2.3.1. Auquel des
modèles 1 ou 2 est liée la loi fondamentale de la statique des fluides ?
Modèle 2 : la masse volumique de l'air est constante, quelle que soit
l'altitude.
2.3.2. Au vu des
graphiques ci-dessus, l’utilisation de cette loi pour répondre à la
question 2.2 parait-elle justifiée ?
Pour une altitude de 10 m les deux modèles donnent la même valeur.
Pour une altitude de 1600 m :
- suivant le modèle 1 : P=1013 (1-0,0065 x4600/288)5,255
=834,97 hPa.
- suivant le modèle 2 : P = 1013-0,1201 x1600 =820,84 hPa.
Ecart relatif : (834,97 -820,84) / 827 ~0,017 ( 1,7 %).
L'écart étant très faible, l'utilisation de la loi fondamentale de la
statique des fluides est justifiée.
|
Réalisation
d'une végétation métallique.
En chimie, une végétation métallique est un type de
dendrites produites par certaines transformations chimiques.
On s’intéresse dans cet
exercice à la modélisation du phénomène de « végétations métalliques » à l’aide des outils de la
chimie moderne, en s’interrogeant notamment
sur la nature de ce métal
qui se dépose comme les feuilles d’un arbre.
Les alchimistes décrivent l’arbre de Diane comme une végétation
d’argent se déposant sur un tronc fait en cuivre.
On souhaite fabriquer un arbre de Diane au laboratoire. Pour ce faire,
on place un fil de cuivre, de masse initiale m’ = 5,6 g dans un bécher
contenant V = 220 mL d’une
solution de nitrate d’argent à la concentration en quantité de matière
égale à c = 0,10 mol.L-1.
1. Préparation de la
solution métallique pour réaliser l’arbre de Diane.
Pour les chimistes, l’eau est un solvant très utilisé. Ses propriétés
sont utilisées dans la réalisation de la végétation métallique car
l’eau est capable de dissoudre le nitrate
d’argent AgNO3 (s) et les autres ions intervenant dans le
phénomène.
1.1. Donner le
schéma de Lewis d’une molécule d’eau, justifier sa forme coudée et
indiquer ses propriétés en lien avec les électronégativités des atomes
qui la
constituent.
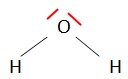
La répulsion entre les doublets non liants conduit à une forme en V.
L'atome d'oxygène plus électronégatif que l'atome d'hydrogène, porte
une charge partielle négative. La molécule d'eau est polaire.
1.2. Écrire
l’équation de la réaction modélisant la dissolution du nitrate d’argent
dans l’eau. Préciser l’état physique des différentes espèces chimiques.
AgNO3(s) ---> Ag+aq +NO3-aq.
1.3. On note c la
concentration en quantité de matière apportée en nitrate d’argent dans
une solution. Exprimer, en fonction de c, la concentration en ions
argent
dissous [Ag+], si la dissolution est totale.
[Ag+] = C.
1.4. En déduire la
quantité de matière n d’ions argent Ag+ contenue dans 250 mL
de la solution de nitrate d’argent de concentration c = 0,10 mol.L-1
et indiquer
la masse m de nitrate d’argent nécessaire pour préparer cette solution.
n = 0,25 x 0,10 = 0,025 mol.
n(AgNO3) = 0,025 mol ; M(AgNO3) =107,9 +14+3x16=
169,9 g / mol.
Masse de nitrate d'argent : 0,025 x169,9 ~4,2 g.
1.5. Proposer un
protocole pour préparer cette solution avec le matériel et les éléments
de verrerie usuels au laboratoire, dont on précisera le nom et le
volume si nécessaire.
Sur une balance placer une coupelle et appuyer sur tare. A l'aide d'une
spatule, verser 4,2 g de nitrate d'argent dans la coupelle.
Verser le solide dans une fiole jaugée de 250 mL surmontée d'un
entonnoir et contenant 1 /3 d'eau distillée. Rincer la coupelle à l'eau
distillée et verser cette eau dans la fiole jaugée.
Agiter pour dissoudre le solide. Compléter jusqu'au trait de jauge à
l'aide d'eau distillée.
2. Modélisation de
la transformation chimique intervenant dans l’arbre de Diane.
On réalise l’expérience, et on prend en photos le système chimique dans
son état initial et dans son état final. Dans l’état initial, la
solution est incolore. Après plusieurs heures, la solution se colore
progressivement en bleu, et le fil de cuivre se recouvre d’un solide
brillant déposé sous forme de " feuillage métallique », qui porte le nom d’«arbre de
Diane» .
2.1. Justifier
qu’une transformation chimique a bien eu lieu.
La solution est initialement incolore et finalement bleue. Le cuivre se
recouvre d'un solide brillant. Une transformation chimique s'est donc
produit.
2.2. Identifier les
couples mis en jeu lors de la formation d’un arbre de Diane et écrire
les deux demi-équations correspondantes.
Cu(s) ---> Cu2+aq +2e- (1).
2Ag+aq +2e- ---> 2 Ag(s) (2).
2.3. En déduire que
l’équation de la réaction modélisant la formation de l’arbre de Diane
s’écrit : 2Ag+ (aq) + Cu (s) → 2Ag (s) + Cu2+ (aq)
(1) +(2) donne : 2Ag+aq
+2e- +Cu(s)
---> 2 Ag(s)Cu2+aq +2e- .
Simplifier : 2Ag+
(aq) + Cu (s) ---> 2Ag (s) + Cu2+ (aq).
2.4. Avec la
méthode de votre choix, montrer que le cuivre est en excès. La quantité
initiale n d’ions argent sera prise égale à 2,2x10-2 mol.
m(cuivre) = 5,6 g ; M(cuivre) = 63,5 g / mol ; 5,6 / 63,5 =0,088 mol.
1 mole de cuivre réagit avec 2 moles d'ion argent.
0,022 mol d'ion argent réagit avec 0,011 mol de cuivre.
Le cuivre est en excès de 0,088-0,011 = 0,077 mol.
2.5. Avec la
méthode de votre choix, déterminer la masse d’argent qui se forme sur
le fil de cuivre si l’avancement maximal est atteint.
|
avancement
(mol)
|
2Ag+ (aq) |
+ Cu (s) |
---> 2Ag (s) |
+ Cu2+ (aq) |
initial
|
0
|
0,022
|
0,088
|
0
|
0
|
en
cours
|
x
|
0,022-2x
|
0,088-x
|
2x
|
x
|
fin
|
xmax
= 0,011
|
0
|
0,077
|
0,022
|
0,011
|
Masse d'argent : 0,022
M(Ag) = 0,022 x 107,9 ~2,4 g.
3. Prévision de
l’état final à l’aide d’un script en Python
Le programme suivant, écrit en langage Python, permet de calculer la
masse d’argent déposée sur le fil de cuivre.

Ce programme permet aussi de s’assurer que le cuivre est bien introduit
en excès :
dans le cas contraire, le fil, qui joue aussi le rôle de support,
risquerait de casser et l’on perdrait la végétation métallique qui met
plusieurs heures à se former.
On exécute le programme. Tout d’abord on indique les conditions
expérimentales initiales de l’expérience décrites précédemment. On
obtient l’écran suivant :
Masse du fil en g : 5,6
concentration de la solution de nitrate d'argent en mol / L : 0,1
volume de la solution en mL : 220.
Écrire la ligne qui apparaîtrait dans la console d’exécution à la suite
de la saisie des données initiales ci-dessus. Justifier.
Le cuivre étant en
excès, la ligne " La masse d'argent déposée vaut : 2,4 g "
apparaît dans la console.
|
|
|



