Physique
chimie, performances d'un cycliste, le littoral sous surveillance,
cloche de plongée.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Performance
d'un cycliste.
1. Étude mécanique du
système S : {Vélo + cycliste}.
On commence par s’intéresser à une portion de route rectiligne
d'inclinaison constante : dans la réalité, on peut estimer que la route
est une succession de portions de route de ce type. De plus, pour
passer de la réalité de la course à un modèle physique simple, on
choisit les hypothèses simplificatrices suivantes :
- on néglige les frottements avec l’air et le contact sol-roue avant ;
- on considère que la valeur de la vitesse de Froome reste constante
sur cette portion rectiligne d'inclinaison constante ;
- on néglige la contribution de la rotation des roues à l’énergie
cinétique totale.
1.1.Définir le
référentiel adapté à l'étude du mouvement du système S.
Le référentiel terrestre, supposé galiléen est le plus adapté.
1.2.Représenter les
forces extérieures agissant sur ce système.
Le système est soumis à son poids et à l'action du support.
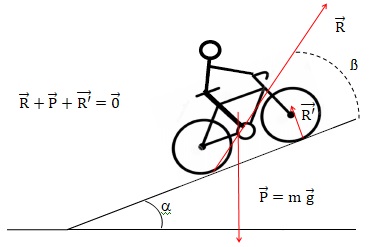
1.3.Compte tenu de
la nature du mouvement de l'ensemble {Vélo + cycliste}, que peut-on en
déduire sur la résultante des forces ? Écrire la relation
correspondante entre vecteurs.
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces
est nulle ( 1ère loi de Newton).
1.4.En projetant
sur un axe défini par la piste, en déduire que c'est la réaction
tangentielle du sol sur la roue arrière qui « empêche le système de
ralentir ».
- m g sin a + R
cos ß = 0 ; R cos ß =
m g sin a
.
2. Étude énergétique du
système {Vélo + cycliste} et simulation numérique.
L’objectif est d’estimer avec nos hypothèses simplificatrices la valeur
de la vitesse du cycliste.
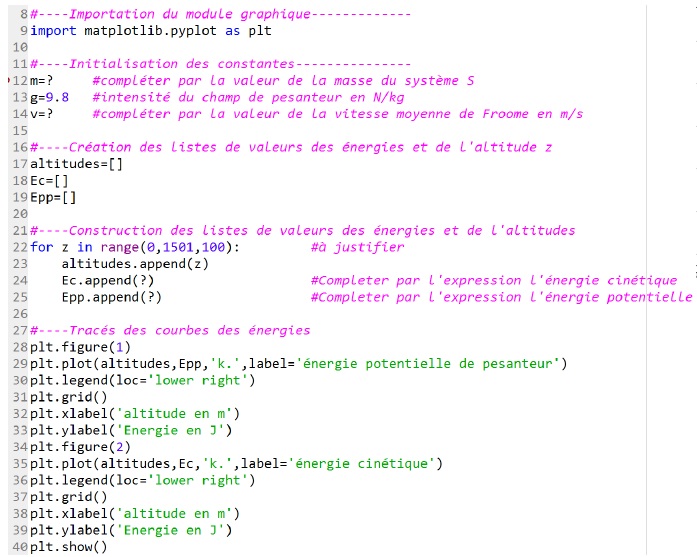
Une simulation écrite en langage Python pour analyser l’évolution des
énergies est donnée.
Voici les résultats obtenus :
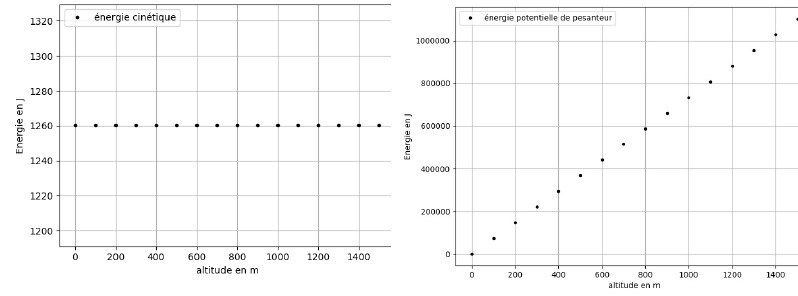
Le code du programme est incomplet.
2.1.Répondre aux
questions en respectant les contraintes suivantes :
- l'origine des altitudes correspond au point A : point de départ de la
course ;
- la piste est rectiligne et d'inclinaison constante jusqu'au point
d'arrivée B de la course ;
- l'origine de l'énergie potentielle de pesanteur est aussi le point A ;
- on veut construire un graphique composé d'un point tous les 100
mètres.
Rappel : +, - ,* , /, ** désignent respectivement l'addition, la
soustraction, la multiplication, la division et l'exponentiation des
nombres (flottants ici).
2.2.Le programme en
Python permet d'obtenir les deux graphiques ci-dessus. Justifier
l’évolution observée de l’énergie cinétique.
La vitesse du cycliste est constante ; l'énergie cinétique du cycliste
½mv2 est donc constante.
2.3.Donner
l’expression de la variation d’énergie potentielle de pesanteur sur
cette portion de piste en fonction notamment de la longueur AB de la
piste et de son inclinaison caractérisée par l’angle α que la piste
fait avec la ligne horizontale.
L'énergie potentielle initiale en A est nulle ( c'est l'origine).
L'énergie potentielle finale en B vaut m g AB sin a.
On note m = masse du cycliste + masse du vélo = m1 + m2.
Variation de l'énergie potentielle entre A et B : m g AB sin a.
On
admet qu’en l’absence de glissement des roues du vélo sur la route, la
réaction R du sol sur les roues ne travaille pas. On prend en compte la
puissance musculaire fournie au système par Christopher Froome par
l’intermédiaire du pédalage : Pmusculaire.
2.4.Faire un bilan
d'énergie mécanique pour le système et en déduire la relation suivante :
Pmusculaire.Δt = (m1 + m2).g.
AB.sin(α).
Energie mise en oeuvre par le cycliste pendant la dure Dt : Pmusculaire.Δt .
L'énergie mécanique du système augmente de l'énergie musculaire mise en
oeuvre. L'énergie cinétique étant constante :
Pmusculaire.Δt
= (m1 + m2).g. AB.sin(α).
2.5. Estimer la
vitesse moyenne de Christopher Froome dans le cadre de ce modèle.
m1 + m2 = 75 kg ; dénivelé AB.sin(α) = 1,5 103
m ; puissance / masse = 5,7 W / kg. AB = 20 km.
Puissance musculaire = 5,7 x 68 = 387,6 W.
Dt = (m1 + m2).g.
AB.sin(α) / Pmusculaire= 75 x 9,8 x1500 /
387,6 ~2,8 103 s.
Vitesse moyenne : 20 103 / (2,8 103) =7,1 m /s ou
7,1 x3,6 =25,7 km / h.
2.6.Comparer
à la valeur de la vitesse moyenne de Froome donnée par l'énoncé (
20,869 km / h) en proposant une critique du modèle adopté.
Il faudrait prendre en compte les forces de frotements exercées par la
route sur les roues du vélo.
numéro
de la ligne du code python
|
le
symbole ? est remplcé par :
|
12
|
75
|
14
|
5.797
|
24
|
0,5*m*v**2
|
25
|
m*g*z
|
Ligne 22 : Pourquoi écrit-on : range (0,1501,100) ?
Réponse : la fonction range génère une suite arithmétique ; la deuxième
valeur ne fait pas partie de la liste.
La premièe valeur est 0, la dernière est 1500 et le pas est de 100.
altidues : 0 ; 100 ; 200 ; 300 ; ...1500.
|
|
Le
littoral sous surveillance.
Le sonar utilise un signal acoustique (en général ultrasonore).
Le lidar (light detection and ranging) utilise un signal
électromagnétique obtenu par technologie laser.
Cet exercice se propose d’étudier quelques aspects de ces techniques.
Partie 1 : le sondeur
acoustique bathymétrique monofaisceau.
Le sondeur émet, sous forme d’impulsions, une onde ultrasonore de
fréquence réglable. Cette onde se propage vers le bas, à la verticale
du bateau. Après réflexion sur le fond marin, elle est captée par le
sondeur qui mesure la durée mise par le signal pour effectuer
l’aller-retour
. Connaissant la célérité des ultrasons dans l’eau, il est possible
d’en déduire la profondeur du fond sous-marin. Le déplacement du
sondeur en surface permet d’obtenir une succession de mesures.
Le technicien qui utilise le sondeur peut modifier la fréquence des
ultrasons en fonction de la profondeur du fond sous-marin qu’il désire
étudier.
Plein océan : 10 kHz ; grands fonds : 40 kHz ; plateaux continentaux :
200 kHz ; petits fonds : 400 kHz.
La célérité des ultrasons dépend de la salinité et de la température de
l’eau de mer.
1.1. Les ondes
ultrasonores sont des ondes mécaniques. Rappeler la définition d’une
onde mécanique progressive. Parmi les deux schémas a et b proposés
ci-dessous, lequel modélise le mieux la propagation des ultrasons ?
Justifier.
Une onde mécanique progressive est la propagation d'une perturbation
dans un milieu matériel avec transport d'énergie, sans transport de
matière.
Les ultrasons sont des ondes mécaniques longitudinales.

1.2. Le signal
simulé ci-dessous possède les mêmes caractéristiques temporelles que
celles du signal émis par le sondeur acoustique prévu pour effectuer
des mesures près du littoral. Les réglages effectués sont-ils cohérents
avec l’utilisation prévue ?
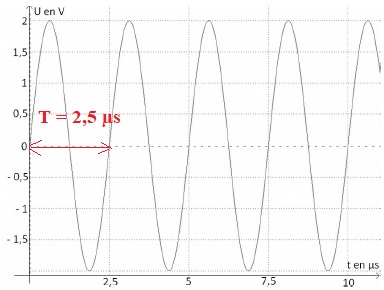
Fréquence = 1 / T = 1 /(2,5 10-6) =4,0 105 Hz
=400 kHz.
Le réglage est cohérent pour les petits fonds.
1.3. Les valeurs
moyennes de température et de salinité de la mer à Toulon au mois de
mai sont les suivantes : température 16 °C, salinité 35 g / L.
1.3.1. Déterminer,
dans ces conditions, la valeur de la célérité des ultrasons dans l’eau
de mer.
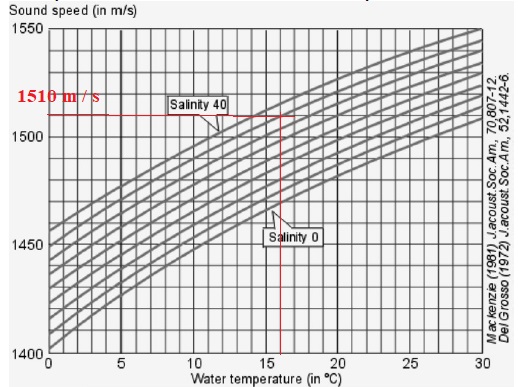
Célérité du son (en m/s) en fonction de la température (en °C) et de la
salinité (en g/L).
Welcome to SIMRAD Training Course Basic Acoustic By Kjell Eger
Kongsberg Maritime
AS, Simrad
1.3.2. Lors de la
mesure, le retard Δt entre l’émission et la réception du signal vaut Δt
= 50,9 ms. La mesure correspond-elle à une mesure effectuée au-dessus
d’une profondeur correspondant à la zone A ou à la zone B, repérées sur
la carte ci-dessous ? Justifier la réponse par un calcul.
Profondeur = c Dt
/ 2 = 1510 x 50,9 10-3 / 2 ~38 m ; il s'agit de la
profondeur de la zone A.
1.4. On s’intéresse
dans cette question aux mesures faites pour la zone de 42 mètres de
profondeur. Cette zone se trouvant à moins de 300 mètres du littoral,
la règlementation maritime exige que la vitesse d’un navire doive
rester inférieure à 3 noeuds. Dans les zones de fonds inférieurs à 100
mètres où la hauteur d’eau sous quille est peu critique, l’incertitude
horizontale totale acceptée est : IHT = 5 mètres + 5 % de la profondeur.
Le fabriquant présente dans sa documentation un fonctionnement du
sondeur à 10 impulsions par seconde : ce fonctionnement vous paraît-il
adapté aux mesures pour la zone de 42 mètres de profondeur ?
1 noeud = 1 mile
nautique par heure ; 1 mile nautique = 1,852 km.
Vitesse maximale du
bateau : 3 x1852 / 3600 =1,54 m /s.
Entre chaque impulsions, le bateau se déplace de 0,15 m, valeur
inférieure à IHT = 5+0,05 x42= 7,1 m.
Ce fonctionnement est adapté.
Partie 2 : le LIDAR.
Le principe de télémétrie du lidar est similaire à celui du sonar :
l’onde électromagnétique émise se réfléchit sur une surface (le sol ou
le fond marin) ; la mesure de la durée mise par le signal pour
effectuer l’aller-retour permet de calculer la hauteur ou la
profondeur, connaissant la vitesse de propagation de l’onde dans le
milieu considéré (air ou eau).
Un lidar topographique utilise une seule longueur d’onde (en général λ
= 1064 nm) alors qu’un lidar bathymétrique émet deux longueurs d’onde
différentes : λ = 1064 nm (qui se réfléchit à la surface de l’eau) et λ
= 534 nm (qui pénètre dans l’eau et se réfléchit sur le fond marin)
Cette partie s’intéresse au rayonnement issu d’un laser de type YAG
dopé au néodyme (laser Nd-YAG).
2.1. À quel domaine
de longueurs d’ondes appartient le rayonnement émis par le laser Nd-
YAG ? Justifier.
1064 nm appartient au proche infrarouge.
2.2. Calculer la
valeur de l’énergie d’un photon émis par le laser Nd-YAG.
E = h c / l =6,63
10-34 x 3,0 108 / (1064 10-9) =1,87 10-19
J ou 1,87 10-19 /(1,6 10-19) =1,17 eV.
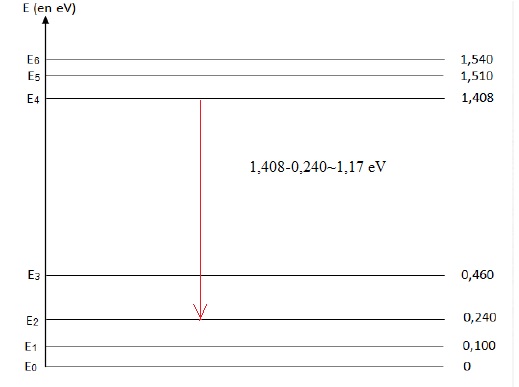
2.3. Un diagramme
énergétique simplifié de la partie émission du laser Nd-YAG est fourni.
2.3.1. Vérifier,
par un calcul, que les niveaux d’énergie mis en jeu lors de l’émission
du faisceau laser sont les niveaux E2 et E4.
2.3.2. Représenter
cette transition par une flèche sur le diagramme.
2.4. Déterminer
l’ordre de grandeur du nombre maximal de photons émis pendant une
impulsion.
Energie maximale par impulsion : 150 J.
150 / (1,87 10-19) ~8,0 1020.
|
Cloche de
plongée.
On modélise une cloche de plongée par un cylindre sans plancher dont la
surface de la base S est égale à 1,0 m² et la hauteur H à 2,4 m.
Avant d'être immergée dans l'eau, la cloche est entièrement remplie
d'air à la pression atmosphérique patm = 1,013 105 Pa. On
considère que la quantité d’air, ainsi que la
température, restent constantes au cours de l'immersion de la cloche.
Données : masse volumique de l’eau de mer dans laquelle la cloche est
immergée : ρ = 1,02 103 kg.m-3 ;
1. Étude expérimentale de
la loi de Mariotte.
Pour modéliser le comportement de l’air dans la cloche, on utilise une
seringue reliée à un appareil de mesure de la pression. La pression P
de l’air emprisonné dans la seringue est relevée pour différentes
valeurs du volume V du corps de la seringue. On suppose que la
température de l’air reste constante.
Les résultats obtenus sont rassemblés dans le tableau ci-dessous :
P(hPa)
|
1011
|
1127
|
1261
|
1419
|
1633
|
1932
|
V(mL)
|
50
|
45
|
40
|
35
|
30
|
25
|
1.1. Quelle précaution doit-on
prendre pour s’assurer que la température de l’air reste la même lors
de chaque mesure ?
Pousser très lentement le piston de la seringue.
1.2. Énoncer la loi
de Mariotte relative au produit de la pression P par le volume V d’un
gaz pour une quantité de matière donnée et une température constante.
Pour une masse de gaz donnée, prise à température constante, le produit
de la pression du gaz par son volume est constant.
1.3.On utilise un
programme écrit en langage Python pour tracer la courbe donnant la
pression P en fonction de l’inverse du volume V. Un extrait de ce
programme est donné
ci-après.

Le tracé obtenu suite à l’exécution du programme est reproduit ci-après
:
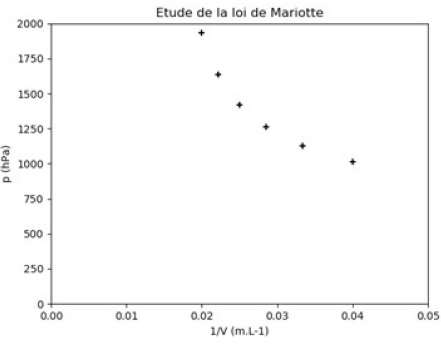
1.3.1. La courbe
obtenue est-elle cohérente avec la loi de Mariotte ? Justifier.
Non la courbe d'équation P = f(1 / V) est une droite.
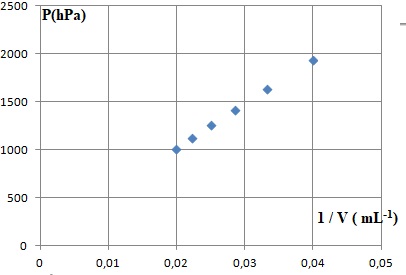
1.3.2. Identifier
l’erreur commise dans le programme. ( voir ci-dessus).
1.4.Exploiter, par
une méthode au choix, les résultats expérimentaux obtenus afin de
tester la loi de Mariotte.
P(hPa)
|
1011
|
1127
|
1261
|
1419
|
1633
|
1932
|
V(mL)
|
50
|
45
|
40
|
35
|
30
|
25
|
P
V ( hPa mL)
|
50
550
|
50715
|
50
440
|
49
665
|
48990
|
48300
|
Le produit P V est à peu
près constant.
2. Fonctionnement de la
cloche de plongée
2.1.Force pressante
exercée par l’eau de mer sur la surface horizontale supérieure de la
cloche immergée à 18 m de profondeur.
2.1.1. La loi
fondamentale de la statique des fluides reliant la différence de
pression pA - pB entre deux points A et B d’un
fluide incompressible à r,
g, et zB – zA , s’écrit
pA - pB = r.g.(zB
– zA) ; zA et zB étant les ordonnées
des points A et B sur un axe des z orienté suivant la verticale
ascendant. Décrire, en le justifiant, l’évolution de
la pression en fonction de la profondeur.
La pression augmente lorsque zB
– zA, c'est à dire la profondeur, croît.
2.1.2. Montrer que la pression p18
de l'eau de mer à 18 m de profondeur est égale à 2,8 105 Pa.
pA - patm
=1,02 103 x9,81 x18 =1,8 105 Pa.
pA= 1,8 105
+1,0 105 = 2,8 105 Pa.
2.1.3. En déduire la valeur de la
force pressante F qui modélise l’action exercée par l’eau de mer sur la
surface horizontale supérieure d’aire S de la cloche immergée
à 18 m de profondeur.
F = P S = 2,8 105 x1 = 2,8 105 N.
2.1.4. Montrer que
la valeur de cette force pressante est égale à celle du poids d'une
masse environ égale à 29 t. Commenter.
m = 2,8 105 / 9,81 ~ 2,9 104 kg soit 29 tonnes.
La cloche doit être particulièrement résistante.
2.2.En comparant
qualitativement la pression de l’air dans la cloche immergée et la
pression atmosphérique, expliquer pourquoi le niveau de l’eau à
l’intérieur de la cloche augmente
lorsque celle-ci est immergée.
La pression de l'air à l'intérieur de la cloche est supérieure à
la pression atmosphérique. A température constante, pour une masse
d'air constante, le volume d'air diminue si la pression augmente.
On considère que la quantité d’air, ainsi que la température, restent
constantes au cours de l'immersion de la cloche.
2.3.On néglige la
variation de la pression de l’eau sur la hauteur de la cloche.
2.3.1. Déterminer
la valeur du volume d’air V0 contenu initialement dans la
cloche cylindrique de section S et de hauteur H.
V0 = S H = 1 x2,4 = 2,4 m3.
2.3.2. Déterminer,
en utilisant la loi de Mariotte, le volume V18 d’air contenu
dans la cloche à 18 m de profondeur.
Patm V0 = P18 V18 ; V18 =Patm V0 / P18 =2,4 / 2,8 ~0,86 m3.
2.3.3. En déduire de quelle hauteur h18
est montée l'eau dans la cloche.
V18 = S x hauteur d'air dans la cloche ; hauteur d'air
=0,86 / 1 = 0,86 m.
h18 = 2,4 -0,86 ~1,5 m.
|
|
|









