E3C première, structure cristalline du diamant, gamme tempérée et guitare classique.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

Structure cristalline du diamant.
On cherche à savoir si, dans le cas du diamant, le carbone cristallise sous une forme cubique à face centrée.
Données :
• Rayon d’un atome de carbone : r = 70 pm
• Masse d’un atome de carbone : m = 2,0x10-26 kg.
3- Étude d’un réseau cubique à faces centrées.
3-a Compléter le schéma de maille d’un réseau cubique à faces centrées en indiquant la position des atomes.

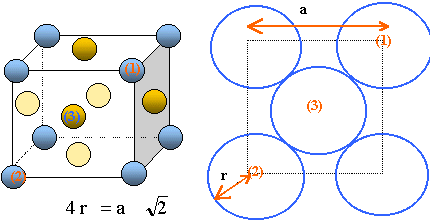Il y a contact des sphères suivant la diagonale d'une face du cube.
3-b Déterminer, en le justifiant, le nombre d’atomes présents à l’intérieur d’une maille.
Chaque maille compte en propre :
- Chaque atome situé au centre d'une face, donc commun à deux mailles compte pour ½ : il y a 6 faces soit 6*0,5 = 3 atomes.
- Chaque atome situé à un sommet, donc commun à huit mailles compte pour 1/8 : il y a huit sommets donc 8 /8  = 1 atome.
Donc 4 atomes par maille.
3-c Le paramètre de maille, noté a, est la longueur d’une arête du cube. Démontrer que a = 2√2𝑟.
Il y a contact des sphères suivant la diagonale d'une face du cube.
4 r = 2½a : a =2 *2½r.
3-d Montrer que la masse volumique r qu’aurait le diamant s’il possédait une structure cubique à faces centrées vérifierait approximativement la formule r =0,18 m / r3.
avec m : masse d’un atome de carbone et r : rayon d’un atome de carbone modélisée par une sphère.
Masse d'une maille : 4 m.
Volume d'une maille : V = a3=(2 *2½r)3 ~22,63 r3.
Masse volumique  : 4 m / (22,63 r3) ~0,18 m / r3.
4- La masse volumique du diamant est 3,51x 103 kg.m-3. Indiquer si le diamant possède une structure cubique à face centrée.
0,18 x2,0 10-26 / (70 10-12)3~10,5 103 kg m-3.
Le diamant ne possède pas une structure cubique à faces centrées.

Recherche de la profondeur de formation du diamant.
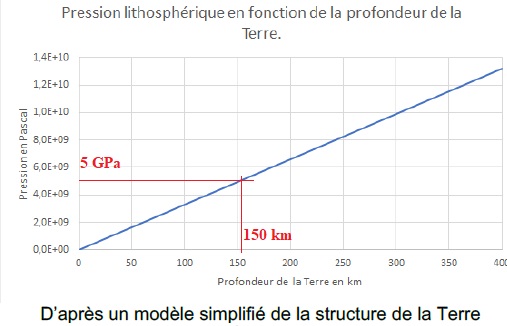
Le carbone pur est présent dans la nature sous deux formes principales : le diamant, qui est transparent, et le graphite, qui est gris et opaque. En laboratoire, il est possible de fabriquer artificiellement du diamant à partir du graphite en modifiant les paramètres de pression et de température : le diamant peut être produit si la pression est comprise entre 5 et 12 GPa . (1 GPa = 1x109 Pa).
5- Estimer la profondeur minimale à partir de laquelle les diamants peuvent se former.




Gamme tempérée et guitare classique. ( d'après bac S 2012)
Partie A. Gamme tempérée.
Il y a eu dans l’histoire de nombreuses méthodes de construction de gammes pour ordonner les notes à l’intérieur d’une octave.
On peut diviser l’octave en douze intervalles à l’aide de treize notes de base (Do, Do#, Ré, Mib, Mi, Fa, Fa#, Sol, Sol#, La, Sib, Si, Do). La gamme fréquemment utilisée de nos jours est la gamme au tempérament égal (ou gamme tempérée), dans laquelle le rapport de fréquences entre deux notes consécutives est constant.
1- Rappeler la valeur du rapport des fréquences de deux notes situées aux extrémités d’une octave.
Chaque note d’une gamme est caractérisée par sa fréquence. Par convention, le La3 (diapason des musiciens) de l’octave numérotée 3 a une fréquence de 440 Hz.
  Le passage d’une note à la note du même nom à l’octave supérieure multiplie sa fréquence par deux ; ainsi la fréquence du La2 est égale à 220 Hz et celle du La4 à 880 Hz.
2- Expliquer pourquoi la valeur exacte du rapport des fréquences entre deux notes consécutives de la gamme tempérée est 21/12.
Dans la gamme tempérée, le quotient de la fréquence d’une note sur la fréquence de la note précédente est égal à
21/12=1,059. Si l’on note f la fréquence de la note Do, note fondamentale d’une octave donnée, les fréquences des notes successives de cette octave sont regroupées dans  le tableau suivant :
DoDo# RébRéRé# MibMi FabMi# FaSolSol# LabLaLa# SibSi DobDo Si#
f1,059 f1,122 f1,189 f1,260 f1,335 f1,498 f1,587 f1,682 f1,782 f1,888 f2f

3- Le tableau  indique les fréquences (en Hertz), arrondies au dixième, de quelques notes de la gamme tempérée.
NoteMi3Fa3Fa# 3SolSol# 3La3Si3bSi3
 D04
fréquence ( Hz)
329,6349,2370,0392,0...440,0466,2
493,9
 523,3

f = 392,0 x 21/12=415,3 Hz.

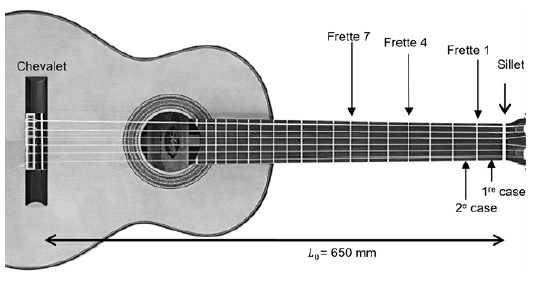
Partie B. Application aux frettes de la guitare classique.
En observant le manche d’une guitare classique, on remarque que les barrettes métalliques, appelées frettes, situées sur les cordes, ne sont pas espacées régulièrement : plus on s’approche du chevalet, plus elles sont resserrées.
Cette partie se propose d’expliquer pourquoi.

4- Lorsqu’on joue à vide la corde la plus fine de la guitare, le son émis est le Mi3.
Pour obtenir un Mi4 le joueur pince cette même corde au niveau de la 12e case (située juste au-dessus de la 12e frette), ce qui produit un son de fréquence
f12 = 2 x f0.
4-a- Le Mi4 est-il plus aigu ou plus grave que le Mi3 ?
f12 = 2 x 329,6 =659,2 Hz.
659,2 > 329,6, le Mi4 est plus aigu que le Mi3.
4-b- Parmi les réponses suivantes, indiquer celle quelle qui correspond à la longueur L12 correspondant à la fréquence f12. Justifier la réponse.
 2L0 ; 0,5 L0 ; 2 / L0.
Sans pincer la corde au niveau d’une case, la corde qui vibre, de longueur L0, produit un son d’une fréquence f0.
Lorsqu’il pince la corde au niveau de la case n, située juste au- dessus de la n-ième frette, la corde qui vibre, de longueur Ln, émet un son de fréquence fn.
Ln × fn = L0 × f0 ; Ln = L0 × f0 /  fn avec f0 /  f12 =0,5 ; L12 = L0 / 2.
5- Longueur de la 1ère case.
Pour obtenir un Fa3, on pince la corde au niveau de la première case, la longueur de la corde vibrante étant alors égale à L1.
Sachant que L1 = L0 / 1,05946, donner l’expression de la longueur de la première case en fonction de L0.
L0 =65,0 cm.
Distance du manche à la frette n° 1 : f1 / f =1,05946 = L / L1 ; L1  =  L /1,05946 = 65,0 / 1,05946 =61,35 cm.
Longueur de la première case : L0-L1= L0-L0 / 1,05946 =0,0561 L0.
 soit 65,0x0,0561 = 3,65 cm.
 

.


  

menu