Jeux et physique : le tic tac, enseignement de spécialité, classe de première générale. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .. ..... Partie 1 : Etude du tic tac.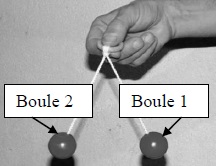 Dans ce qui suit, on appelle : - boule 1 la boule située à droite sur la photographie - boule 2 la boule située à gauche sur la photographie. A Étude énergétique de la boule 1. On modélise ici le jeu par un pendule simple constitué de la boule 1 de masse m=80 g, suspendue à un fil inextensible de masse négligeable et de longueur L = 20 cm. Le fil est accroché au point I et les mouvements du pendule s’effectuent dans un plan vertical. Le joueur écarte la boule 1 d’un angle α m Le centre de la boule 1 est ainsi situé au point G. Le joueur lâche la boule 1 sans vitesse initiale. Le mouvement du pendule est étudié dans le repère (G 0 , x, z) orienté comme l’indique la figure ci dessous ; axe G0 z est vertical On néglige les frottements. 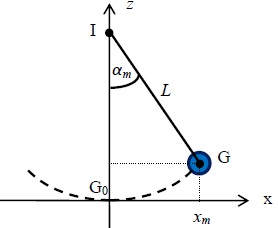Données - l’énergie potentielle de pesanteur est choisie nulle au point G0 le plus bas de la trajectoire - la valeur de l’intensité de la pesanteur est g = 9,8 N.kg-1. A.1. On s’intéresse à la boule 1 lorsqu’ elle est à une hauteur z et possède une vitesse v . Rappeler les expressions - de son é nergie cinétique Ec - de son énergie potentielle de pesanteur Epp - de son énergie mécanique Em en fonction de m , g , z et v. Ec = ½mv2 ; Epp = mgz ; Em = ½mv2 + mgz. A.2. On modélise expérimentalement la situation en utilisant un montage comprenant un capteur , un pendule simple de même caractéristique que la partie du tac tac associée à la boule 1 On peut alors tracer les variations des trois types d'énergie (en mJ) précé dentes en fonction de l'abscisse x (en mm) du centre de la boule 1 pour seulement une partie de la trajectoire de la boule 1 . 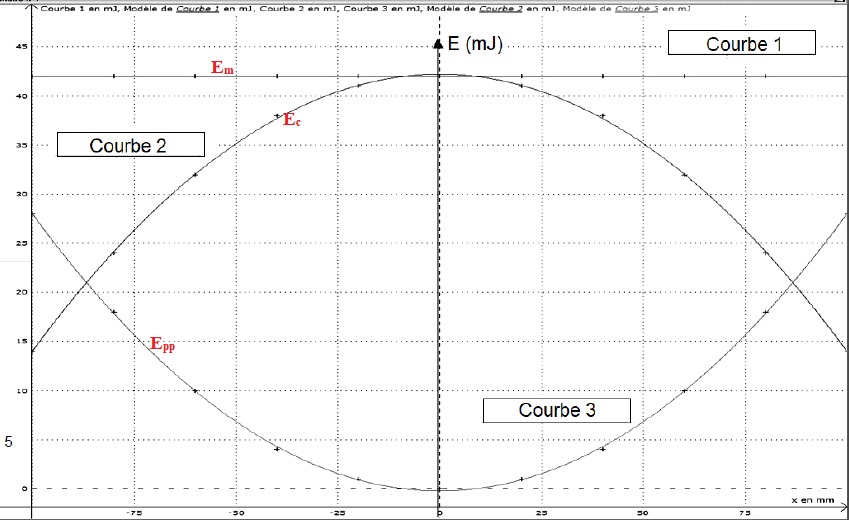On obtient les courbes suivantes : Associer, en justifiant la réponse , chaque courbe à l’énergie Ec , Epp ou Em dont elle représente les variations. L'énergie mécanique est constante en abscence de frottement : courbe 1. L'énergie potentielle initiale décroît avec l'altitude z, s'annule au passage en G0, puis croît : courbe 3. L'énergie cinétique augmente au cours de la descente, passe par un maximum en G0, puis décroït : courbe 2. .. ... . . B. Étude du choc entre les deux boules. 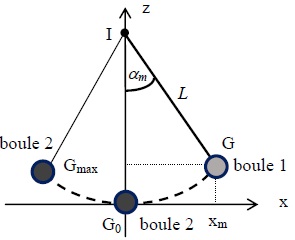O n lâche sans vitesse initiale la boule 1 du point G . A u point G0 un choc se produit entre la boule 1 et la boule 2 qui initialement est au repos. La boule 2 se met en mouvement. On suppose qu ’au point G0 et juste avant le choc la boule 1 possède la vitesse maximale vG0 =1,0 m.s-1 et une énergie mécanique de 42 mJ. Au cours du choc entre les deux boules, il se produit une dissipation d'énergie mécanique E dis =15 mJ. Juste après le choc, la boule 1 est au repos et la boule 2 se met en mouvement vers la gauche pour atteindre, avant de redescendre, un point extrême Gmax dont on veut déterminer l’altitude zGmax. B.1.Calculer l'énergie mécanique Em2,G0 de la boule 2 en G0 juste après le choc. Em2,G0 =42-15=27 mJ. B.2. Expliquer pourquoi l’énergie cinétique de la boule 2 au point Gmax est nulle. Si la vitesse de la boule 2 n'était pas nulle au point Gmax, la boule 2 monterait plus haut. Or Gmax est le point le plus haut atteint par la boule 2. B.3. Exprimer l'énergie mécanique Em2,Gmax de la boule 2 au point G max en fonction de m, g et z G max. La vitesse étant nulle en ce point, l'énergie mécanique est sous forme potentielle de pesanteur. Em2,Gmax = m g z G max. B.4. En supposant que l 'énergie mécanique de la boule 2 reste constante au cours de son mouvement calculer la valeur de l’altitude z G max. Conclure. L'énergie mécanique se conserve : z G max = Em2,G0 /(mg) = 27 10-3 / (0,080 x9,8) =0,0344 m ~ 34 mm. Au départ de la boule 1, son énergie mécanique est sous forme potentielle : 0,042 = 0,080 x9,8 h ; h ~0,054 mou 54 mm. z G max est inférieure à l'altitude initiale de la boule 1, du fait de la dissipation de l'énergie mécanique au cours du choc. . . .   .

menu