� l’�tat microscopique, l’argent m�tallique solide est organis� selon un r�seau cubique � faces centr�es.
1- Montrer en
explicitant la d�marche que le nombre d’atomes contenus dans une maille
�l�mentaire du cristal d’argent est �gal � 4.
2- En notant a le param�tre de maille du cristal d’argent (�gal � la longueur de l’ar�te du cube), d�montrer que a 2�=4r. En d�duire que a=4,10 10-10 m.
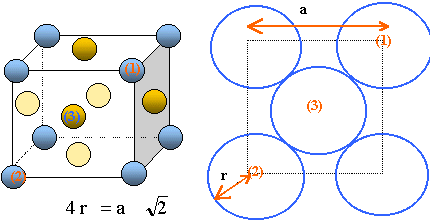
il y a contact des sph�res suivant la diagonale d'une
face du cube.
Rayon moyen d’un atome d’argent : r = 1,45 10-10 m.
a =4 x1,45 10-10 / 2� =4,10 10-10 m.
3- Calculer
la compacit� du cristal d’argent et en d�duire que 26 % de la maille
�l�mentaire est vide. On rappelle que la compacit� d’un cristal est
�gale au rapport du volume des atomes contenus dans une maille
�l�mentaire par le volume de cette maille.
- Chaque atome situ� au centre d'une face, donc
commun � deux mailles compte pour � : il y a 6 faces soit 6*0,5 = 3
atomes d'argent.
- Chaque atome situ� � un sommet, donc commun � huit
mailles compte pour 1/8 : il y a huit sommets donc un atome d'argent.
Total : 4 atomes d'argent par maille.
Volume des atomes consid�r�s comme des sph�res dures : V = 4 * 4 / 3 *3,14 *(1,45 10-10)3 =5,11 10-29 m3.
Volume de la maille : (4,10 * 10-10)3 =6,89 10-29 m3.
Compacit� : 5,11 / 6,89 =0,74.
1-0,74 = 0,26.
26 % de la maille �l�mentaire est vide.
4- La masse volumique de l’argent sous forme cristalline vaut approximativement 10,5�103 kg∙m-3. Calculer la masse d’un atome d’argent apr�s avoir d�termin� le volume d’une maille du cristal.
Volume de la maille : (4,10 * 10-10)3 =6,89 10-29 m3.
Masse de la maille =masse de 4 atomes d'argent : 6,89 10-29 x 10,5�103 =7,23 10-25 kg.
Masse d'un atome d'argent :7,23 10-25 / 4 =1,81 10-25 kg.
5- La
chlorargyrite et l’acanthite sont des cristaux. Pr�ciser le sens du mot
cristal et donner un exemple d’un autre mode d’organisation de la
mati�re solide � l’�chelle microscopique.
Dans un cristal, les atomes ou les ions sont parfaitement organis�s selon une structure g�om�trique bien d�finie.
Exemple d’un autre mode d’organisation de la mati�re solide � l’�chelle microscopique : un verre poss�de une structure amorphe.
6- Expliquer pourquoi le minerai d’Ain-Kerma peut �tre qualifi� de roche et pourquoi cette roche peut �tre qualifi�e d’argentif�re.
Une
roche naturelle est g�n�ralement solide et form�e d'un asemblage de
min�raux, comportant parfois des fossiles, du verre r�sultant d'un
refroidissement rapide d'un liquide.
Un minerai contenant des traces d'argent peut �tre qualifi� de roche argentif�re.
