Mathématiques,
E3C première Amérique du Nord 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1, QCM (
5 points).
Question 1.
Pour tout réel x, e2x+e4x est égal à :
e6x ; e2x(1+e2) ; e3x(ex+e-x)vrai ; exp(8x2).
y = 7(x-1) vrai.; y = x-1 ; y
=7x+7 ; y = x+1.
e3x(ex+e-x) = e3x+x +e3x-x.
Question 2.
Dans le plan muni d'un repère orthonormé, on considère les vecteurs
suivants de coordonnées respectives (-5 ; 2) et (4 ; 10) ainsi que la
droite (d) d'équation 5x+2y+3=0.
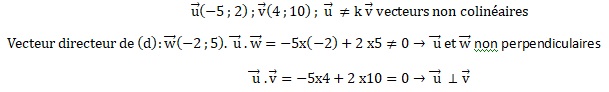
Réponse c.
Question 3.
La dérivée f ' de la fonction f définie sur R par f(x) =(2x-1)e-x
est :
2xe-x ; -2e-x ; (-2x+3)e-x vrai ; 2e-x +(2x-1)e-x.
On pose u = 2x-1 et v = e-x ; u' = 2 ; v' = -e-x.
u'v+v'u = 2e-x-(2x-1)e-x =
(-2x+3)e-x.
Question 4. Pour
tout réel x, on a : sin(p+x)
=
- sin(x) vrai ; cos(x) ;
sin(x) ; -cos(x).
Question 5.
Soit f une fonction définie et dérivable sur R dont la courbe
représentative est donnée. La tangente à cette courbe au point A est la
droite T.
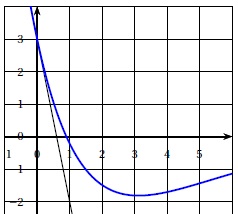
f '(0) = 3 ; f '(0) = 1/5 ; f '(0) = 5 ; f '(0) = -5 vrai.
La pente de la tangente en A d'abscisse zéro est égale à -5 : f '(0) =
-5.
Exercice 2. 5
points.
La population d'une ville augmente chaque année de 2%. La ville a 4600
habitants en 2010.
La population d'une ville B augmente de 110 habitants par an. B a 5100
habitants en 2010.
1. Calculer le
nombre d'habitants de chaque ville fin 2011.
A : 4600 x1,02 =4692.
B 5100+110=5210.
On note un le nombre d'habitants de A et vn le
nombre d'habitants de B.
2. Quelle est la nature des suite (un)
et (vn) ?
(un) suite géométrique de raison 1,02 et de premier terme
4600.
(vn) suite arithmétique de raison 110 et de premier terme
5100.
3. Exprimer un
en fonction de n. Calculer le nombre d'habitants de A en 2020.
un =4600 x 1,02n. u10 =4600 x1,0210
~5607.
4. Exprimer vn en fonction de n.
Calculer le nombre d'habitants de B en 2020.
vn =5100 x 110 n. v10 =5100 +1100
=6200.
5.
Compléter l'algorithme suivant. Au bout de combien d'année la
population de la ville A dépasserat-elle celle de la ville B ?
def année()
u =4600
v=5100
n=0
while u < v :
u = u*1,02
v=v+110
n = n+1.
return n
u32= 8669 ; v32 =8620.
Année 2042.
|
...
|
....
|
Exercice 3. (5 points)
Soit h la fonction définie sur [0 ; 26) par :
h(x) = -x3+30x2-108x-490.
1. Exprimer h'(x).
h'(x) =-3x2 +60x-108.
On note C la courbe représentative de h et C'
celle de h'.
2. Identifier C et C' en justifiant.
-3x2 +60x-108 =0.
Discriminant D= 602-4*108*3=2304
=482.
Solutions x1 = (-60+48) / (-6) =2 ; x1
= (-60-48) / (-6) =18.
h'(x) >0 si x appartient à [2 ; 18] et h(x) est croissante sur cet
intervalle.
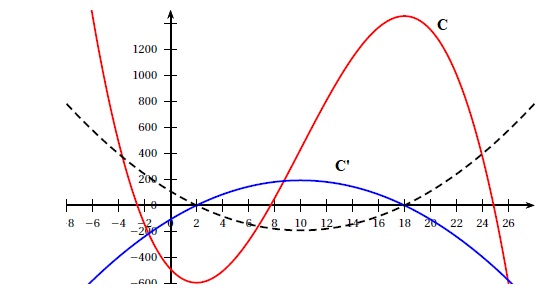
3. Soit T la tangente au point A
d'abscisse zéro. Déterminer son équation réduite.
h'(0) =-108.
Equation de T : y = -108x +b.
Le point de coordonnées (0 ; h(0) =-490) appartient à la tangente.
-490 = b; y = -108x-490.
4. Etudier le signe de h'(x) puis
dresser le tableau de variation de la fonction h.
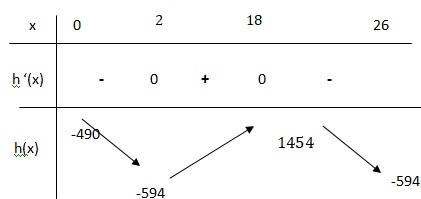
Exercice 4. 5 points.
Une entreprise qui fabrique des aiguilles dispose de 2 sites de
production A et B.
A produit les trois-quart des aiguilles et 2 % sont défectueuses.
B produit un quart des
aiguilles et 4 % sont défectueuses.
Les aiguilles provenant des deux sites sont mélangées et vendues
ensemble par lots.
On choisit une aiguille dans la production et on considère les
événements :
A : l'aiguille provient du site A.
B : l'aiguille provient du
site B.
D : l'aiguille présente un défaut.
1. Déterminer lP(A) :
P(A) = 0,75.
2. Compléter
l'arbre suivant :
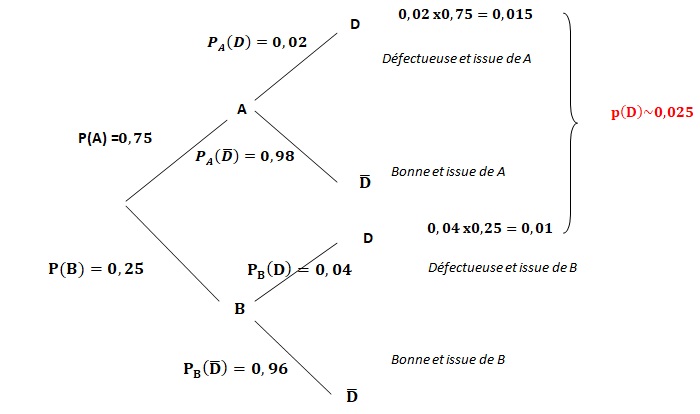
3. Quelle est la probabilité que
l'aiguille ait un défaut et provienne de A ,
P(A n D) = 0,75 x0,02 = 0,015.
4. Montrer que p(D) = 0,025.
Formule des probabilités totales.
5. Après
inspection, l'aiguille choisie est défectueuse. Quelle est la
probabilité qu'elle provienne de A ?
PD(A) = P(A n D) / P(D) =0,015 / 0,025 =0,6.
|
|