Mathématiques,
suites et fonctions, Bac Asie
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Un médicament est administré à un patient par voie intraveineuse.
Partie A : modèle discret de la quantité médicamenteuse
Après une première injection de 1 mg de médicament, le patient est placé sous perfusion.
On estime que, toutes les 30 minutes, l’organisme du patient élimine 10 % de la quantité de
médicament présente dans le sang et qu’il reçoit une dose supplémentaire de 0,25 mg de la
substance médicamenteuse.
On étudie l’évolution de la quantité de médicament dans le sang avec le modèle suivant :
pour tout entier naturel n, on note u n la quantité, en mg, de médicament dans le sang du
patient au bout de n périodes de trente minutes. On a donc u 0 = 1.
1. Calculer la quantité de médicament dans le sang au bout d’une demi-heure.
1 -0,1+0,25 = 1,15 mg.
2. Justifier que, pour tout entier naturel n, u n+1 = 0,9u n +0,25.
A chaque demi-heure, 0,1 u n disparaît (il reste donc 0,9 u n) et on ajoute 0,25 mg.
3. a. Montrer par récurrence sur n que, pour tout entier naturel n, u n< u n+1 < 5.
Initialisation : u0 < u1 < 5. est vraie.
Hérédité : la relation est supposée vraie eau rang n.
un< un+1 < 5.
0,9 un< 0,9 un+1 < 0,9 x5 = 4,5.
0,9 un +0,25< 0,9 un+1 +0,25 < 0,9 x5 +0,25= 4,75
un+1 < un+2 <4,75 < 5
La relation est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
b. En déduire que la suite (u n) est convergente.
u n+1 > u n la suite est croissante.
un+1 < 5 la suite est majorée.
La suite est croissante et majorée, donc elle converge.
4. On estime que le médicament est réellement efficace lorsque sa quantité dans le sang
du patient est supérieure ou égale à 1,8 mg.
a. Recopier et
compléter le script écrit en langage Python suivant de manière à
déterminer au bout de combien de périodes de trente minutes le
médicament commence à être réellement efficace.
def efficace():
u=1
n=0
whileu <1.8
u= 0,9 u +0,25
n = n+1
return n
b. Quelle est la valeur renvoyée par ce script ? Interpréter ce résultat dans le contexte
de l’exercice.
u 2 =1,15 x0,9 +0,25 =1,285 mg ; u3 =1,285 x0,9 +0,25 =1,4065 mg ;
u4 =1,4065 x0,9 +0,25 =1,5159 mg ; u5 =1,45159 x0,9 +0,25 =1,614 mg ;
u6 =1,614 x0,9 +0,25 =1,7029 mg ; u7 =1,7029 x0,9 +0,25 =1,7826 mg ;
u8 =1,7826 x0,9 +0,25 =1,85 mg.
Le script renvoie n = 8. Au bout de 4 heures, le médicament est efficace.
5. Soit (v n) la suite définie, pour tout entier naturel n, par v n = 2,5−u n.
a. Montrer que (v n) est une suite géométrique dont on précisera la raison et le premier terme (v 0).
vn+1 = 2,5−un+1 = 2,5 -0,9un +0,25= 2,25 -0,9 un = 0,9(2,5 -un) = 0,9 vn.
Raison q = 0,9 ; v0 =2,5-1=1,5.
b. Montrer que, pour tout entier naturel n, u n = 2,5−1,5×0,9 n
.
v n = 1,5 x 0,9 n= 2,5−un.
un = 2,5−1,5×0,9n
.
c. Le médicament devient toxique lorsque sa quantité présente dans le sang du patient dépasse 3 mg.
D’après le modèle choisi, le traitement présente-t-il un risque pour le patient ?
Justifier.
-1 < 0,9 < 1, donc 0,9 n tend vers zéro si n tend vers plus l'infini.
u n tend vers 2,5 mg, valeur inférieure à 3 mg. Le médicament ne peut pas devenir toxique.
Partie B : modèle continu de la quantité médicamenteuse
Après une injection initiale de 1 mg de médicament, le patient est placé sous perfusion.
Le débit de la substance médicamenteuse administrée au patient est de 0,5 mg par heure.
La quantité de médicament dans le sang du patient, en fonction du temps, est modélisée par
la fonction f , définie sur [0 ; +∞[, par
f (t) = 2,5−1,5e −0,2t
,
où t désigne la durée de la perfusion exprimée en heure.
On rappelle que ce médicament est réellement efficace lorsque sa quantité dans le sang du
patient est supérieure ou égale à 1,8 mg.
1. Le médicament est-il réellement efficace au bout de 3 h 45 min ?
3 h45 min = 3,75 h.
f (3,75) = 2,5−1,5e−0,2x 3,75 = 1,79 mg. Traitement pas encore efficace.
2. Selon ce modèle, déterminer au bout de combien de temps le médicament devient
réellement efficace.
2,5−1,5e−0,2t > 1,8 ; 1,5e−0,2t <0,7 ; e−0,2t < 0,7 /1,5.
-0,2 t < ln(0,7 / 1,5) ; t > ln(0,7 / 1,5) / 0,2 ; t > 3,81 h ou 3 h 47 min.
3. Comparer le résultat obtenu avec celui obtenu à la question 4. b. du modèle discret de
la Partie A.
Cette perfusion est plus rapidement efficace que la précédente.
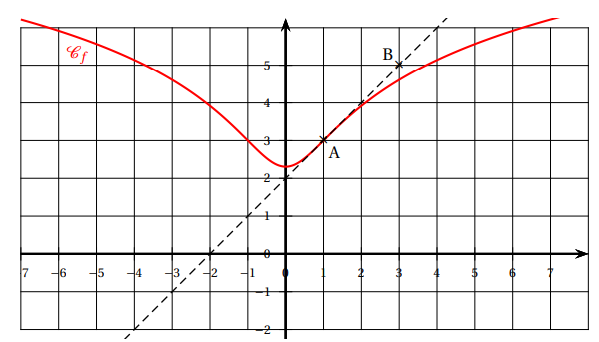
Soit f une fonction définie et dérivable sur R. On considère les points A(1; 3) et B(3; 5).
On donne ci-dessous C f
la courbe représentative de f dans un repère orthogonal du plan,
ainsi que la tangente (AB) à la courbe C f au point A.
 Partie A
1.
Partie A
1. Déterminer graphiquement les valeurs de f (1) et f
′
(1).
f(1) = 3 ; f '(1) = 1 ; coefficient directeur de T.
2. La fonction f est définie par l’expression f (x) = ln(
ax 2 +1 )
+ b, où a et b sont des
nombres réels positifs.
a. Déterminer l’expression de f
′
(x).
f '(x) = 2ax / (ax 2+1).
b. Déterminer les valeurs de a et b à l’aide des résultats précédents.
f(1) = ln(a+1)+b =3 ; f '(1) =2a / (a 2+1) = 1.
a 2+1-2a = 0 ; (a-1) 2=0 soit a = 1.
Par suite : b = 3-ln(2).
Partie B
On admet que la fonction f est définie sur R par
f (x) = ln(
x
2 +1 )
+3−ln(2).
1. Montrer que f est une fonction paire.
f(-x) = ln(
(-x)
2 +1 )
+3−ln(2)= ln(
x
2 +1 )
+3−ln(2) = f(x).
2. Déterminer les limites de f en +∞ et en −∞.
En plus l'infini : x2+1 tend vers plus l'infini ; ln(
x
2 +1 ) tend vers plus l'infini ; f(x) tend vers plus l'infini.
En moins l'infini : x2+1 tend vers plus l'infini ; ln(
x
2 +1 ) tend vers plus l'infini ; f(x) tend vers plus l'infini.
3. Déterminer l’expression de f
′
(x).
Étudier le sens de variation de la fonction f sur R.
Dresser le tableau des variations de f en y faisant figurer la valeur exacte du minimum
ainsi que les limites de f en −∞ et +∞.
f '(x) = 2x / (x 2+1).
f '(x) a le signe de x.
Si x < 0 : f '(x) < 0 et f(x) est décroissante.
Si x > 0 : f '(x) > 0 et f(x) est croissante.
Si x = 0, f '(x) est nulle ; la fonction présente un minimum : f(0) = 3-ln(2).
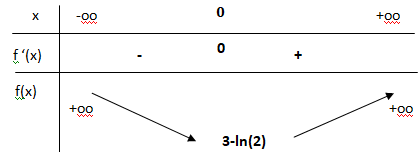
4. À l’aide du tableau des variations de f , donner les valeurs du réel k pour lesquelles
l’équation f (x) = k admet deux solutions.
Il faut que k soit supérieur à 3-ln(2).
5. Résoudre l’équation f (x) = 3+ln 2.
ln(
x
2 +1 )
+3−ln(2) = 3+ ln(2).
ln(
x
2 +1 )=2 ln(2) = ln (4).
x2+1 = 4 ; x2 = 3 ; x = ±3½.
Partie C.
1. Conjecturer, par lecture graphique, les abscisses des éventuels points d’inflexion de la
courbe C f
.
Deux points d'inflexion aux abscisse -1 et +1.
2. Montrer que, pour tout nombre réel x, on a : f
′′(x) =
2(
1− x
2) / (
x
2 +1 ) 2.
f '(x) = 2x / (x2+1).
On dérive, on pose u = 2x ; v = x2+1 ; u' = 2 ; v' = 2x.
(u'v-v'u) / v2 =(2(x2+1) -4x2) / (
x
2 +1 )2 =2(
1− x
2) / (
x
2 +1 )2.
3. En déduire le plus grand intervalle sur lequel la fonction f est convexe.
f "(x) >0 sur [-1 ; +1], la fonction est convexe sur cet intervalle.
|
...
|
....
|
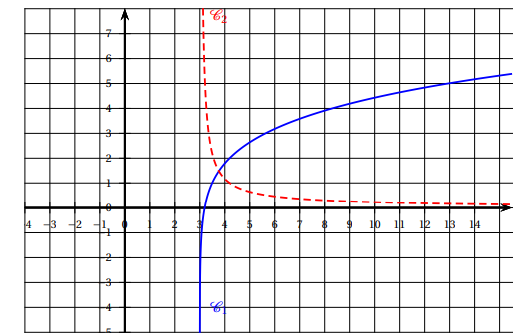
Dans le repère orthonormé ci-dessus, sont tracées les courbes
représentatives d’une fonction f et de sa fonction dérivée, notée f
′
, toutes deux définies sur ]3 ; +∞[.
1. Associer à chaque courbe la fonction qu’elle représente. Justifier.
Courbe bleue, fonction croissante. Cela implique une dérivée positive ( courbe rouge en pointillés).
2. Déterminer graphiquement la ou les solutions éventuelles de l’équation f (x) = 3.
f(x) = 3 ; x ~5,6, une seule solution.
3. Indiquer, par lecture graphique, la convexité de la fonction f .
La courbe est toujours en dessous de ces tangentes, donc fonction concave.
Partie B
1. Justifier que la quantité ln(
x
2 − x −6 )
est bien définie pour les valeurs x de l’intervalle
]3 ; +∞[, que l’on nommera I dans la suite.
x2-x-6 = 0; discriminant D =1+6*4=25=52.
Racines : x1 = (1+5) / 2 = 3 et x2 = (1-5)/ 2 = -2.
x
2 − x −6 >0 sur ]-oo ; -2[ union ]3 ; +oo[.
2. On admet que la fonction f de la Partie A est définie par f (x) = ln(
x2
− x −6 )
sur I.
Calculer les limites de la fonction f aux deux bornes de l’intervalle I.
En déduire une équation d’une asymptote à la courbe représentative de la fonction f
sur I.
x tend vers 3 :
x
2 − x −6 tend vers zéro et f(x) tend vers moins l'infini.
La droite d'équation x = 3 est asymptote.
x tend vers plus l'infini : f(x) tend vers plus l'infini.
3. a. Calculer f
′
(x) pour tout x appartenant à I.
f '(x) = (2x-1) / (x2-x-6).
b. Étudier le sens de variation de la fonction f sur I.
Dresser le tableau des variations de la fonction f en y faisant figurer les limites
aux bornes de I.
f'(x) a le signe de 2x-1 ; sur ]3 ; +oo[ f '(x) est strictement positive et f(x) est strictement croissante.
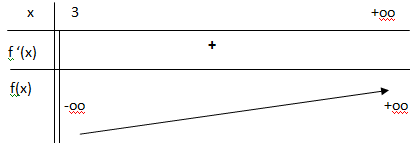
4. a. Justifier que l’équation f (x) = 3 admet une unique solution a sur l’intervalle
]5; 6[.
f(5)=ln(14) ~2,64 ; f(6) =ln(24)~3,18.
Sur l'intervalle ]5 ; 6 [, f(x) est strictement croissante de ln(14) à ln(24).
f étant continue car dérivable, f (x) = 3 admet une unique solution a sur l’intervalle
]5; 6[.
b. Déterminer, à l’aide de la calculatrice, un encadrement de a à 10−2 près.
5,63 < a < 5,64.
5. a. Justifier que f
′′(x) =
(−2x
2 +2x −13) / (
x
2 − x −6 )2
.
f '(x) = (2x-1) / (x2-x-6). On dérive en posant u = 2x-1 et v = x2-x-6.
u'=2 ; v'=2x-1.
(u'v-v'u) / v2 = [2( x2-x-6)-(2x-1)(2x-1)] / (
x
2 − x −6 )2
.
Le numérateur s'écrit : 2x2-2x-12 -4x2-1+4x=−2x
2 +2x −13.
b. Étudier la convexité de la fonction f sur I.
f "(x) a le signe de −2x
2 +2x −13 :
Racinces sde −2x
2 +2x −13 =0
Discriminant D = 4-8*13 < 0. Aucune racine réelle.
−2x
2 +2x −13 < 0 ; f "(x) < 0 : la fonction est concave.
Partie 1
Julien doit prendre l’avion; il a prévu de prendre le bus pour se rendre à l’aéroport.
S’il prend le bus de 8 h, il est sûr d’être à l’aéroport à temps pour son vol.
Par contre, le bus suivant ne lui permettrait pas d’arriver à temps à l’aéroport.
Julien est parti en retard de son appartement et la probabilité qu’il manque son bus est de
0,8.
S’il manque son bus, il se rend à l’aéroport en prenant une compagnie de voitures privées; il
a alors une probabilité de 0,5 d’être à l’heure à l’aéroport.
On notera : - B l’évènement : « Julien réussit à prendre son bus » ;
- V l’évènement : « Julien est à l’heure à l’aéroport pour son vol ».
1. Donner la valeur de PB (V ).
En prenant le bus, il est sûr d'arriver à l'heure ; PB(V) = 1.
2. Représenter la situation par un arbre pondéré.
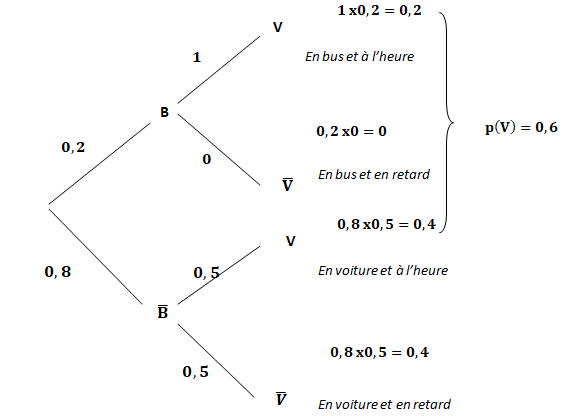
3. Montrer que P(V ) = 0,6.
P(V) = PB(V) +P(non B(V) = 0,2 +04 = 0,6.
4. Si Julien est à l’heure à l’aéroport pour son vol, quelle est la probabilité qu’il soit arrivé
à l’aéroport en bus ? Justifier.
PV(B) =P(B n V) / (P(V) =0,2 / 0,6 = 1 /3.
Partie 2
Les compagnies aériennes vendent plus de billets qu’il n’y a de places
dans les avions car
certains passagers ne se présentent pas à l’embarquement du vol sur
lequel ils ont réservé.
On appelle cette pratique le surbooking.
Au vu des statistiques des vols précédents, la compagnie aérienne
estime que chaque passager a 5 % de chance de ne pas se présenter à
l’embarquement.
Considérons un vol dans un avion de 200 places pour lequel 206 billets
ont été vendus. On
suppose que la présence à l’embarquement de chaque passager est
indépendante des autres
passagers et on appelle X la variable aléatoire qui compte le nombre de
passagers se présentant à l’embarquement.
1. Justifier que X suit une loi binomiale dont on précisera les paramètres.
La présence à l’embarquement d'un passager est indépendante de celle des autres et
chaque passager a la même probabilité 0,95 d’être présent. La variable aléatoire
X suit la loi binomiale de paramètres n = 206 et p = 0,95.
2. En moyenne, combien de passagers vont-ils se présenter à l’embarquement ?
E = np = 206 x0,95 =196.
3. Calculer la probabilité que 201 passagers se présentent à l’embarquement. Le résultat
sera arrondi à 10−3 près.
P(X=201) =(206 201) x 0,95201 x(1-0,95)206=0,306.
4. Calculer P(X < 200), le résultat sera arrondi à 10−3 près. Interpréter ce résultat dans le
contexte de l’exercice.
La calculatrice donne P(X < 200) =0,948.
L'avion est à peu près certain d'être complet.
5. La compagnie aérienne
vend chaque billet à 250 euros.
Si plus de 200 passagers se présentent à l’embarquement, la compagnie
doit rembourser le billet d’avion et payer une pénalité de 600 euros à
chaque passager lésé.
On appelle :
Y la variable aléatoire égale au nombre de passagers qui ne peuvent pas
embarquer
bien qu’ayant acheté un billet ;
C la variable aléatoire qui totalise le chiffre d’affaire de la
compagnie aérienne sur ce
vol.
On admet que Y suit la loi de probabilité donnée par le tableau suivant :
yi
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
P(Y = yi)
|
0,947 75
|
0,030 63
|
0,014 41
|
0,005 39
|
0,001 51
|
0,000 28
|
0,000 03
|
P(C=ci)
|
51 500
|
50 560
|
49 800
|
48 950
|
48 100 |
47 250
|
46 400
|
a. Compléter la loi de probabilité donnée ci-dessus en calculant P(Y = 6).
P(Y=6) = 1-P(Y=0) -P(T=1) -....P(Y=5)=0,000 03
b. Justifier que : C = 51500−850Y .
La compagnie encaisse : 206 x250 = 51 500 €.
Elle remnourse 850 € à chaque client ne pouvant pas embarqué.
C = 51500−850Y .
c. Donner la loi de probabilité de la variable aléatoire C sous forme d’un tableau.
Calculer l’espérance de la variable aléatoire C à l’euro près.
E(C) = 51 500 x0,947 75 +... +46400 x0,000 03 =51 429 €.
d. Comparer le chiffre d’affaires obtenu en vendant exactement 200 billets et le
chiffre d’affaires moyen obtenu en pratiquant le surbooking.
Vente de 200 billets : 200 x250 = 50 000 €.
Pratique du surbooking : gain 51 500 €.
|
|