Modélisation
d'un service au tennis, bac Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
La
balle doit passer en diagonale au-dessus du filet et toucher le sol
dans le carré de service opposé avant que le relanceur ne la renvoie.
Masse de la balle m = 58 g. L'action de l'air sera négligée.
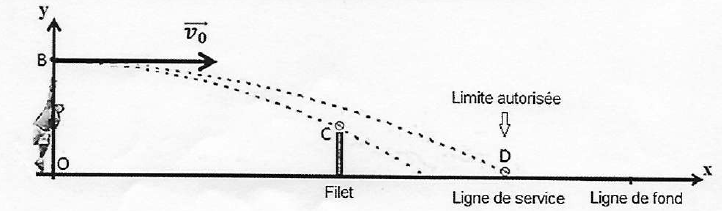
A. Equation de la trajectoire.
Position initiale de la balle , point B(0 ; H).
Vecteur vitesse initiale : (v0 ; 0).
1. Déterminer les coordonnées du vecteur accélération du centre de masse de la balle.
La balle n'étant soumise qu'à son poids, la seconde loi de Newton conduit à : ax = 0 ; ay = -g.
2. Déterminer les composantes du vecteur vitesse.
Le vecteur vitesse est une primitive du vecteur accélération.
vx = v0.
vy = -gt.
3. En déduire que l'équation de la trajectoire de la balle s'écrit : y(x) = -g /(2v 02) x 2+H.
Le vecteur position est une primitive du vecteur vitesse.
x = v 0t ; y = -½gt 2 + H.
t = x / v 0, repport dans y : y(x) = -g /(2v02) x2+H.
B Influence de la vitesse initiale.
Elle doit être supérieure à une valeur minimum v0min afin qu'elle franchisse juste le filet au point C et inférieure à une valeur maximum v0max afin qu'elle retombe rans les limites autorisées au point D.
1. Exprimer la vitesse initiale v 0 en fonction de y(x), x, g et H. H-y(x) = g /(2v02) ; v02 = g / [2(H-y(x)] ; v0 =[ g / [2(H-y(x))] ]½.
2. Déterminer les coordonnées des points C et D.
xC = 5,50 + 6,40 = 11,90 m.
Hauteur centrale du filet yC= 0,91 m.
xD = xC + coté du carré de service =11,90 +4,11 = 16,01 m.
yD = 0 ( sol).
3. Si H = 2,6 m, en déduire v0min et v0max.
v0min =[ 9,81 xC2/ [2(2,6-y(C))] ]½=[ 9,81*11,92 / [2(2,6-0,91)] ]½~ 20 m /s.
v0max =[ 9,81 xD2/ [2(2,6-y(D))] ]½=[ 9,81*162 / [2(2,6-0)] ]½~ 22 m /s.
4. En réalité la vitesse initiale mesurée est bien supérieure aux vitesses calculées précédemment. Commenter.
Le modèle de la chute libre n'est pas valable. Il faut prendre en
compte l'action de l'air et tenir compte de la rotation de la balle.
|
...
|
....
|
C. Etude énergétique.
Les données du mouvement réel de la balle figurent ci-dessous. Montrer que l'action de l'air doit être prise en compte.
t(s)
|
0
|
0,03
|
0,06
|
0,09
|
0,12
|
0,15
|
0,18
|
0,21
|
0,24
|
0,27
|
y(m)
|
2,58
|
2,43
|
2,29
|
2,11
|
1,97
|
1,81
|
1,63
|
1,48
|
1,28
|
1,10
|
v(m /s)
|
47,8
|
44,7
|
43,6
|
42,8
|
41,7
|
40,3
|
39,4
|
37,5
|
36,4
|
35,3
|
Ec = 0,5 mv2 (J)
|
66,3
|
55,9
|
53,2
|
51,3
|
48,7
|
45,5
|
43,4
|
39,4
|
37,1
|
24,5
|
Ep = mgy ( J)
|
1,5
|
1,38
|
1,30
|
1,20
|
1,12
|
1,03
|
0,93
|
0,84
|
0,73
|
0,63
|
Ep + EC = Em
|
67,8
|
57,3
|
54,5
|
52,5
|
49,8
|
46,5
|
44,3
|
40,2
|
37,8
|
25,1
|
L'énergie mécanique de la balle n'étant pas constante, la chute n'est pas libre ; il faut prendre en compte l'action de l'air..
|
|