Mathématiques,
suites et fonctions, bac Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
1. On considère la suite (un) définie pour tout entier naturel n par
un =(−1)n/(n+1)
On peut affirmer que :
a. la suite (un) diverge vers +∞.
b. la suite (un) diverge vers −∞.
c. la suite (un) n’a pas de limite.
d. la suite (un) converge. Vrai.
-1 < (-1)n < 1.
-1/(n+1) < un < 1 / (n+1).
D'après le théorème des gendarmes, un tend vers zéro si n tend vers plus l'infini.
Dans les questions 2 et 3, on considère deux suites (vn) et (wn) vérifiant la relation :
wn = exp(−2vn) +2.
2. Soit a un nombre réel strictement positif. On a v0 = ln(a).
a. w0 =1/a2+2 vrai
b. w0 =1/(a2+2)
c. w0 = −2a +2
d. w0 =1/(−2a)+2.
w0=exp(-2ln(a)) +2 = 1/ exp[2ln(a)] +2 = 1/ exp(ln(a)2)+2 =1/a2+2.
3. On sait que la suite (vn) est croissante. On peut affirmer que la suite (wn) est :
a. décroissante et majorée par 3.
b. décroissante et minorée par 2 . Vrai.
c. croissante et majorée par 3 .
d. croissante etminorée par 2.
vn < vn+1 ; -2vn > -2vn+1 ;
exp(-2vn) > exp(-2vn+1).
wn est donc décroissante ; la fonction exponentielle étant strictement positive, exp(-2vn) > 0 et wn > 2.
4. On considère la suite (an) ainsi définie :
a0 = 2 et, pour tout entier naturel n, an+1 =1 / 3 an + 8 / 3.
Pour tout entier naturel n,on a :
a. an = 4׋(1/3)n-2.
b. an = -2 /3n+4. Vrai
c. an = 4−‹(1/3)n
d. an = 2׋(1/3)n+ 8n/ 3.
Soit la suite (bn) telle que bn = an +ß ; bn+1=1 / 3 an + 8 / 3+ ß= 1 /3(bn-ß)+ 8 / 3+ ß=1/3 bn-ß /3+8 /3 +ß =1/3 bn+(8+2ß) /3.
En prenant ß = -4, bn+1 = bn /3, il s'agit d'une suite géométrique de raison 1 /3 et de premier terme b0 = a0 -4 = -2.
bn= -2(1/3)n ; an =bn-ß =4-2(1/3)n.
5. On considère une suite (bn) telle que, pour tout entier naturel n, on a :
bn+1 = bn +lnŒ [2 / (bn2 +3)].‘
On peut affirmer que :
a. la suite (bn) est croissante.
b. la suite (bn) est décroissante. Vrai
c. la suite (bn) n’est pas monotone.
d. Le sens de variation de la suite (bn) dépend de b0.
bn+1-bn =lnΠ[2 / (bn2 +3)].
bn2 > 0 ; bn2+3 > 3 > 2 ; 2 / (bn2 +3) < 1 ; lnΠ[2 / (bn2 +3)] < 0.
bn+1-bn < 0 , la suite est décroissante.
6. On considère la fonction g définie sur l’intervalle ]0 ; +∞[ par :
g(x) =ex/x.
On note Cg la courbe représentative de la fonction g dans un repère orthogonal.
La courbe Cg admet :
a. une asymptote verticale et une asymptote horizontale.
b. une asymptote verticale et aucune asymptote horizontale. Vrai
c. aucune asymptote verticale et une asymptote horizontale.
d. aucune asymptote verticale et aucune asymptote horizontale.
Si x tend vers O+, ex tend vers 1 et ex /x tend vers +oo ;
si x tend vers O-, ex tend vers 1 et ex /x tend vers -oo ;
l'axe des ordonnées est asymptote verticale à la courbe Cg.
Si x tend vers -oo, ex tend vers zéro et ex /x tend vers zéro.
Si x tend vers +oo, ex tend vers +oo et ex /x tend vers +oo par croissance comparée ; donc pas d'asymptote.
7. Soit f la fonction définie sur R par
f (x) = x exp(x2+1).
Soit F une primitive sur R de la fonction f . Pour tout réel x, on a :
a. F(x) =0,5 x2exp(x2+1).
On dérive en posant u = 0,5 x2 et v = exp(x2+1).
u' = x ; v' =2x exp(x2+1).
u'v +v'u = x exp(x2+1) +x3 exp(x2+1).
b. F(x) =(1+2x2) exp(x2+1).
On dérive en posant u = 1+2 x2 et v = exp(x2+1).
u' = 4x ; v' =2x exp(x2+1).
u'v +v'u = 4x exp(x2+1) +2x(1+2x2) exp(x2+1).
c. F(x) =exp(x2+1).
On dérive : F '(x) =2x exp(x2+1).
d. F(x) =0,5 exp(x2+1). Vrai
On dérive : f(x) =0,5 *2x exp(x2+1)= x exp(x2+1).
|
...
|
....
|
On considère la fonction f définie sur R par
f (x) = x3 e x .
On admet que la fonction f est dérivable sur R et on note f ′ sa fonction dérivée.
1. On définit la suite (un) par u0 = −1 et, pour tout entier naturel n, un+1 = f (un).
a. Calculer u1 puis u2.
On donnera les valeurs exactes, puis les valeurs approchées à 10−3.
u1=f(-1)= -1/e ~ -0,368.
u2 = f(-1/e)=-1/ e3 exp(-1/e) ~ -0,034.
b. On considère la fonction fonc, écrite en langage Python ci-dessous.
On rappelle qu’en langage Python,
« i in range (n) » signifie que i varie de 0 à n -1.
def fonc (n)
u = - 1
for i in range(n):
u=u**3*exp(u)
return u
Déterminer, sans justifier, la valeur renvoyée par fonc (2) arrondie à 10−3.
fonc(2) renvoie u2 ~ -0,034.
2. a. Démontrer que, pour tout x réel, on a f ′(x) = x2 e x (x +3).
On pose u = x3 et v = ex ; u' = 3x2 et v' = ex.
u'v+v'u=(3x2 +x3)ex = x2 e x (x +3).
b. Justifier que le tableau de variations de f sur R est celui représenté ci-dessous :
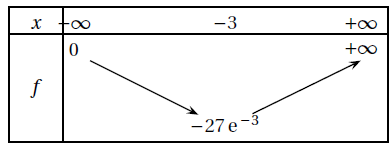
x2 e x étant positif ou nul, f '(x) a le signe de x+3.
Si x < -3, f '(x) <0 et f(x) est strictement décroissante de 0 à f(-3) = -27e-3.
Si x > -3, f '(x) > 0 et f(x) est strictement croissante de -27e-3 à +oo.
Si x = -3, f '(x) = 0 et f(x) présente un minimum.
c. Démontrer, par récurrence, que pour tout entier naturel n, on a : −1< un < un+1 < 0.
Initialisation : u1 = -0,368 ; u2 = -0,034. La prorpiété est vraie au rang zéro.
Hérédité : −1<un <un+1 < 0 est supposée vraie.
La fonction f(x) étant strictement croissante sur ]-3 ; +oo[ :
f(−1) < f(un ) < f(un+1 ) < f(0).
-0,368 < f(un ) < f(un+1 ) < 0.
-0,368 < un+1 < un+2 < 0.
-1 < un+1 < un+2 < 0.
La prorpiété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier n.
d. En déduire que la suite (un) est convergente.
La suite est croissante et bornée par zéro, donc elle converge.
e. On note l la limite de la suite (un).
On rappelle que ℓ est solution de l’équation f (x) = x.
Déterminer ℓ . Pour cela, on admettra que l’équation x2 e x −1 = 0 possède une seule solution dans R et que celle-ci est strictement supérieure à 0,5.
On résout sur [-1 ; 0] l'équation f(x) = x.
x3 e x = x.
x(x2ex - 1)=0.
x = 0 est la seule solution dans [-1 ; 0] car la solution de x2ex - 1 est supérieure à 0,5.
La limite de la suite est donc l = 0.
|
|