Mathématiques, probabilités, bac Nlle Calédonie 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... QCM. On considère un système de communication binaire transmettant des 0 et des 1. Chaque 0 ou 1 est appelé bit. En raison d’interférences, il peut y avoir des erreurs de transmission : un 0 peut être reçu comme un 1 et, de même, un 1 peut être reçu comme un 0. Pour un bit choisi au hasard dans le message, on note les évènements : • E0 : « le bit envoyé est un 0 »; • E1 : « le bit envoyé est un 1 »; • R0 : « le bit reçu est un 0 » • R1 : « le bit reçu est un 1 ». On sait que : p (E0)= 0,4; pR0 (R1) = 0,01; pR1 (R0) = 0,02. On rappelle que la probabilité conditionnelle de A sachant B est notée pB(A). On peut ainsi représenter la situation par l’arbre de probabilités ci-dessous. 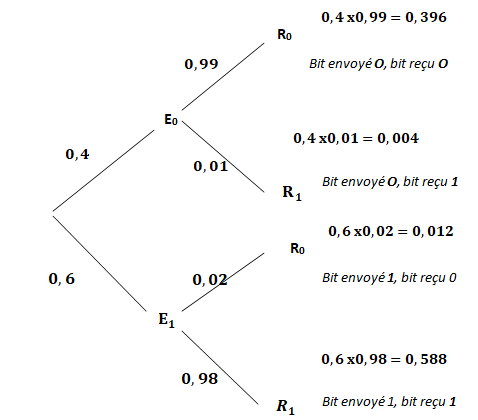1. La probabilité que le bit envoyé soit un 0 et que le bit reçu soit un 0 est égale à : a. 0,99 ; b. 0,396 vrai ; c. 0,01 ; d. 0,4. 2. La probabilité p (R0) est égale à : a. 0,99 ; b. 0,02 ; c. 0,408 vrai ; d. 0,931. Loi des probabilités totales : 0,396 +0,012 =0,408. 3. Une valeur, approchée au millième, de la probabilité pR1 (E0) est égale a. 0,004 ; b. 0,001 ; c. 0,007 vrai ; d. 0,010. p(R1) = 1 - P(R0) =1-0,408=0,592. pR1 (E0)=p(E0 n R1) / P(R1) =0,4 x0,01 / 0,592~0,007. 4. La probabilité de l’évènement « il y a une erreur de transmission » est égale à : a. 0,03 ; b. 0,016 vrai ; c. 0,16 ; d. 0,015. 0,004 +0,012 = 0,016. Un message de longueur huit bits est appelé un octet.  On admet que la probabilité qu’un octet soit transmis sans erreur est égale à 0,88.  5. On transmet successivement 10 octets de façon indépendante. La probabilité , à 10-3 près, qu'exactement 7 octets soient transmis sans erreur est égale à : a.0,03 ; b. 0,016 ; c.0,16 ; d. 0,085 vrai . On a une loi binomiale de paramètres n = 10 et p = 0,88. Si x est la variable aléatoire égal au nombre d’octets transmis sans erreur, on a : p(X = 7) =( 10 7) × 0,887 × (1 − 0,88)10−7  ≈ 0,085. 6. On transmet successivement 10 octets de façon indépendante. La probabilité qu'au moins un octet soit transmis sans erreur est égale à : a. 1-0,1210 vrai; b. $0,12^{10} ; c. 0,8810 ; d. 1-0,8810. p(X > 1) =1-p(X=0=1-0,1210. 7. Soit $N$ N un entier naturel. On transmet successivement $N$ N octets de façon indépendante. Soit $N_0$ N0 la plus grande valeur de $N$ N pour laquelle la probabilité que les $N$ octets soient tous transmis sans erreur est supérieure ou égale à $0,1$0,1. On peut affirmer que : a. N0 = 17 ; b. N0 = 18 vrai ; c. N0 = 19 ; d. N0 = 20.$N_0=17$ On appelle Y la variable aléatoire comptant le nombre d'octets transmis sans erreur. Y suit la loi binomiale ( N ; p = 0,88). P(Y = N) >0,1 ; 0,88N > 0,1 ; N ln( N) > ln (0,1) ; N < ln(0,1) / ln(0,88) ; N0 = 18. ... .... Au basket-bail, il existe deux sortes de tir : — les tirs à deux points. Ils sont réalisés près du panier et rapportent deux points s’ils sont réussis. — les tirs à trois points. Ils sont réalisés loin du panier et rapportent trois points s’ils sont réussis. Stéphanie s’entraîne au tir. On dispose des données suivantes : ● Un quart de ses tirs sont des tirs à deux points. Parmi eux, 60% sont réussis. ● Trois quarts de ses tirs sont des tirs à trois points. Parmi eux, 35 % sont réussis. 1. Stéphanie réalise un tir. On considère les évènements suivants : D : « Il s’agit d’un tir à deux points ». R : « le tir est réussi ». a. Représenter la situation à l’aide d’un arbre de probabilités. 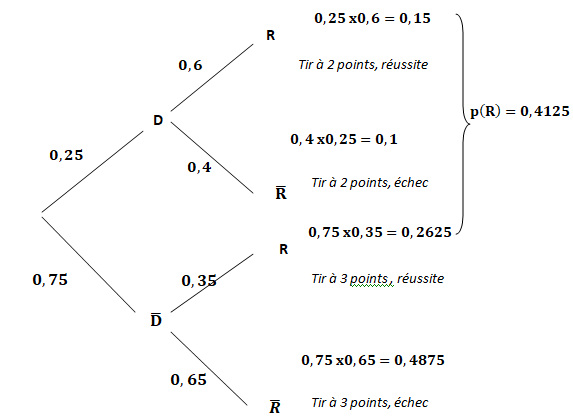b. Calculer la probabilité p (non ‰D ∩RŽ). 0,75 x 0,35=0,2625. c. Démontrer que la probabilité que Stéphanie réussisse un tir est égale à 0,4125. Loi des probabilités totales : 0,15 +0,2625=0,4125. d. Stéphanie réussit un tir. Calculer la probabilité qu’il s’agisse d’un tir à trois points. Arrondir le résultat au centième. PR( non D) = P(R n non D) / P(R) = 0,2625 / 0,4125 ~0,64. 2. Stéphanie réalise à présent une série de 10 tirs à trois points. On considère que les tirs sont indépendants. On rappelle que la probabilité que Stéphanie réussisse un tir à trois points est égale à 0,35. a. Justifier que X suit une loi binomiale. Préciser ses paramètres. On répète 10 fois de manière indépendante la même expérience de Bernoulli. X suit la loi binomiale de paramètres n=10 ; p =0,35. b. Calculer l’espérance de X. Interpréter le résultat dans le contexte de l’exercice. Espérance E(X) = n p = 10 x0,35 = 3,5. Sur 100 tirs à trois points, elle réussit en moyenne 35 tirs. c. Déterminer la probabilité que Stéphanie rate 4 tirs ou plus. Arrondir le résultat au centième. P(X < 6) = 0,97. d. Déterminer la probabilité que Stéphanie rate au plus 4 tirs. Arrondir le résultat au centième. P(X > 6) =1- P(X < 5) ~ 0,09. 3. Soit n un entier naturel non nul. Stéphanie souhaite réaliser une série de n tirs à trois points. On considère que les tirs sont indépendants. On rappelle que la probabilité qu’elle réussisse un tir à trois points est égale à 0,35. Déterminer la valeur minimale de n pour que la probabilité que Stéphanie réussisse au moins un tir parmi les n tirs soit supérieure ou égale à 0,99. Soit Y la variable aléatoire qui compte le nombre de tirs réussis. Y suit la loi binomiale de paramètres n ; p = 0,35. P(Y > 1) > 0,99. 1-P(Y=0) > 0,99. P(Y=0) < 0,01. 0,65n < 0,01. n ln(0,65) < ln(0,01). ln(0,01) / ln(0,65) ~ 10,7. Donc n = 11.

menu