Lunette
afocale, détermination du diamètre de Jupiter,
bac Centres étrangers 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
La
distance entre la Terre et Jupiter étant connue, il est possible de
déterminer son diamètre D si on connait son diamètre apparent aJ
vu à l'oeil nu depuis la Terre.
On note a l'angle sous lequel on
voit l'objet à l'oeil nu.
On note a' l'angle sous lequel on
voit le même objet à travers la lunette.
. Q1. Rappeler la définition
du grossissement G d'une lunette.
G = a' / a.
Observations de Jupiter par Huygens en 1684.
Il estime le grosissement de sa lunette à 164. Avec ce grossissement il
voyait Jupiter à travers la lunette deux fois plus gros qu'il ne voyait
la Lune à l'oeil nu. Le diamètre apparent de la Lune étant connu, il
put estimer que celui de Jupiter était environ aJ = 10-4
radian.
Q2.
Montrer que aJ
= 2 aL
/ G.
aL
: diamètre apparent de la Lune.
" il voyait Jupiter
à travers la lunette deux fois plus gros qu'il ne voyait la Lune à
l'oeil nu "
G aJ =2aL ; aJ = 2 aL / G.
Huygens connaissait la valeur du diamètre apparent de la Lune à l'oeil
nu. aL = 8,7 10-3
rad.
Q3. Montrer que l'on retrouve la
valeur du diamètre apparent de Jupiter trouvé dans un premier temps par
Huygens.
aJ
= 2 aL
/ G = 2 x8,7 10-3 / 164 ~1,1 10-4 rad.
On modèlise la lunette par l'association d'une lentille convergente L1
de grande distance focale f '1 appelée objectif et d'une
lentille convergente L2 de petite distance focale f '2,
appelée oculaire. Le foyer image F'1 coîncide avec le
foyer objet F2 de L2.
On considère un objet AB situé à l'infini représentant Jupiter.
Q4. Indiquer où se
forme l'image intermédiaire A1B1 de l'objet AB
formé par l'objectif. Justifier que l'ensemble des deux lentilles
constitue un système afocal.
Objectif : l'image A1B1
d'un objet à l'infini se trouve au foyer image F'1.
Oculaire :
A1B1 joue le rôle
d'objet pour L2.
Le
foyer image F'1 coîncide avec le foyer objet F2
de L2.
L'image d'un objet situé au foyer objet,
se trouve rejetée à l'infini.
Lunette :
l'image d'un objet à l'infini se trouve à l'infini : le système est
donc afocal.
. Q5. Construire l'image
intermédiaire A1B1.
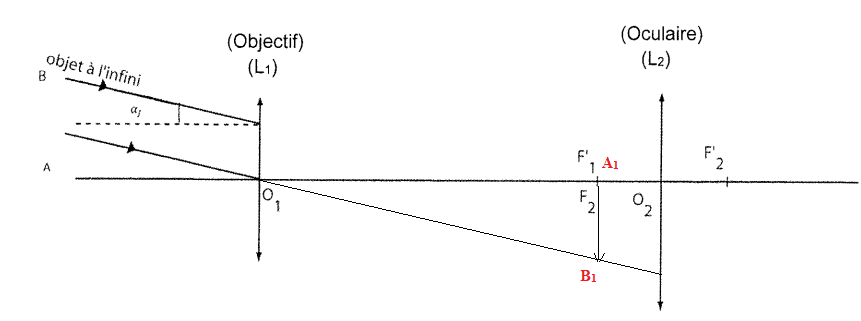
Q6.
Représenter le faisceau émergent issu de B délimité par les deux rayons
incidents déja tracés, et traversant la lunette.
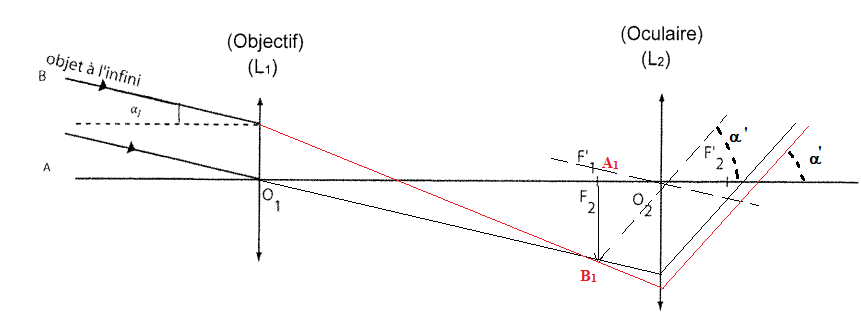
Q7. Exprimer G en
fonction de f '1 et f '2.
Triangle O1A1B1 : tan a ~ a =A1B1
/ f '1.
Triangle O2A1B1
: tan a' ~ a' =A1B1
/ f '2
Par suite G = a'
/ a.=
f '1 / f '2.
Application à la lunette
de Huygens.
f '1 = 10,35 m ; f '2 = 63 mm.
Q8. Expliquer le calcul
effectué par Huygens pour obtenir aJ à partir de la
taille de l'image intermédiaire. ( taille de l'image intermédiaire 2
mm).
aJ
= A1B1 / f '1 =2
10-3 / 10,35 ~ 2 10-4 rad.
Q9.
Calculer le grossissement de cette lunette et expliquer pour quelle
raison la première détermination de aJ ~ 10-4
rad est peu précise.
G = f '1 / f
'2 =10,35 / (63 10-3) ~1,6 102.
Huygens
insère au niveau de l'image intermédiaire de Jupiter créée par
l'objectif, un petit repère afin de mesurer la taille de cette image.
Connaissant de plus la distance focale de l'objectif, il détermine
expérimentalement, avec précision, le diamètre apparent de Jupiter.
La première mesure du diamètre apparent de Jupiter est une estimation à
partir du diamètre apparent de la lune.
Q10. La distance Terre-Jupiter étant
d = 7,80 108 km, calculer la valeur D du diamètre de Jupiter.
aJ
= D / d ; D =7,80 108 x 2 10-4 ~1,6 105
km.
|
|