Table
de tennis connectée, bac Liban 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
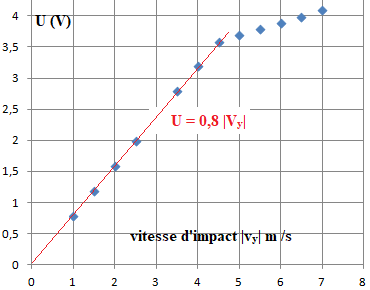
La table identifie les points de chute d'une balle et détermine sa vitesse quand elle touche.
1. Justifier que pour |vy| < 4,5 m/s, la tenion U est proportionnelle avec |vy|.
Un programme python permet l'affichage de la vitessed'impact verticale à partir de U.
Ulim = 3,5
if U < Ulim
v = 1,3*U
else :
v = 5,0*U-13
print ("la vitesse d'impact est ", v, "en m /s")
2. Expliquer la nécessité d'utiliser la variable Ulim = 3,5.
Au delà d'une vitesse d'impact supérieure à 3,5 m/s, la vitesse et la tension ne sont plus proportionnelles..
3. Calculer la vitesse d'impact affichée par ce programme i U = 4,0 V. .
v = 5,0 x4,0=7 m /s., en accord avec le graphique.
Exemple d'utilisation.
On étudie le mouvement d'une balle de ping pong de masse m = 2,7 g qui
évolue dans le champ de pesanteur. On néglige l'action de l'air.
Longueur de la table L = 2,74 m.
O est au bord de la table ; h = OA = 0,10 m. La balle part de A à la vitesse v0 = 5,0 m /s ; a = 30°.
Elle touche la table en I.
La balle est une sphère de diamètre d = 40 mm. On étudie le mouvement de son centre de masse.
4. Justifier la position du centre de masse.
La balle étant homogène, son centre de masse est le centre de la sphère.
5. Indiquer les caractéristiques de la force appliquée à la balle durant son mouvement.
Poids : appliqué en G, centre de masse, verticale, vers le bas, valeur mg =2,7 10-3 x9,8 ~ 2,6 10-2 N.
6. Montrer que les coordonnées du vecteur vitesse sont : vx(t) =v0 cos a et vy(t) = -gt + v0 sin a.
Coordonnées de l'accélération : ax = 0 ; ay = -gt.
La vitesse est une primitive de l'accélération :
vx(t) = Cste ; vy(t) = -gt + autre constante.
Vo(cos a ; v0 sin a.)
Par suite : vx(t) =v0 cos a et vy(t) = -gt + v0 sin a.
7. Déterminer les équations horaires du mouvement.
La position est une primitive de la vitesse.
x(t) = v0 cos a t + cste.
A t = 0, la balle est à x=0 ; par suite : x(t) = v0 cos a t .
y(t) = -½gt2 + v0 sin a.t+ cste.
A t = 0 y(0) = h = 0,10 m.
Par suite : y(t) = -½gt2 + v0 sin a.t+h.
7. L'impact de la balle a lieu à t = 0,55 s.
Montrer que la balle tombe sur la table.
x(0,55) = 5,0 cos 30 x 0,55 =2,38 m.
Cette valeur est inférieure à la longueur de la table.
8.
Les points A et B de ce satellite peuvent-ils être distingué à l'oeil
nu ?
AB = 1 m ; d = 520 km = 5,2 105 m.
a = 1
/ (5,2 105) =1,9 10-6 rad, valeur inférieure au
pouvoir séparateur de l'oeil.
A et B ne sont pas visibles à l'oeil nu.
9. Calculer la tension U délivrée par le capteur au point d'impact.
vy(t) = -gt + v0 sin a.
vy(0,55) =-9,81 x0,55 + 5,0 sin(30) = -2,9 m /s ; |vy| = 2,9 m /s.
U = 0,8 x2,9 =2,3 V.
|