Math�matiques,
suites, fonctions, Bac M�tropole Antilles
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Dans
le cadre d’un essai clinique on envisage deux protocoles de traitement
d’une maladie.
L’objectif de cet exercice est d’�tudier, pour ces deux protocoles,
l’�volution de la quantit� de m�dicament pr�sente dans le sang d’un
patient en fonction du temps.
Les parties A et B sont ind�pendantes.
Partie A : �tude du premier protocole
Le premier protocole consiste � faire absorber un m�dicament, sous forme de comprim�, au patient.
On mod�lise la quantit� de m�dicament pr�sente dans le sang du patient, exprim�e en mg, par la
fonction f d�finie sur l’intervalle [0; 10] par
f (t) = 3te
−0,5t+1
,
o� t d�signe le temps, exprim� en heure, �coul� depuis la prise du comprim�.
1. a. On admet que la fonction f est d�rivable sur l’intervalle [0; 10] et on note f
′
sa fonction
d�riv�e.
Montrer que, pour tout nombre r�el t de [0; 10], on a : f
′
(t) = 3(−0,5t +1)e −0,5t+1
.
On pose u = 3t et v = e -0,5t+1 ; u' = 3 ; v' = -0,5 e-0,5t+1 ;
u'v+v'u = 3e-0,5t+1 -1,5t e-0,5t+1 = 3(−0,5t +1)e−0,5t+1
.
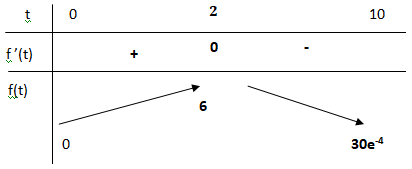
b. En d�duire le tableau de variations de la fonction f sur l’intervalle [0; 10].
3 e -0,5t+1 est positif ; la d�riv�e a le signe de -0,5 t+1.
Si 0 < t < 2, f '(t) > 0 et f(t) est croissante.
Si 2 < t < 10, f '(t) < 0 et f(t) est d�croissante.
Si t = 2, f '(t) =0 et f(t) pr�sente un maximum f(2) = 6.
c. Selon cette
mod�lisation, au bout de combien de temps la quantit� de m�dicament
pr�sente dans le sang du patient sera-t-elle maximale ?
Quelle est alors cette quantit� maximale ?
Au bout de 2 heures, la quantit� est maximale �gale � 6 mg.
2. a. Montrer que l’�quation f (t) = 5 admet une unique solution sur l’intervalle [0; 2] not�e a,
dont on donnera une valeur approch�e � 10 −2 pr�s.
Sur l'intervalle [0 ; 2] la fonction est continue et strictement
croissante � valeurs dans [0 ; 6]. 5 appartient � cet intervalle.
D'apr�s le corollaire du th�or�me des valeurs interm�diaires, l'�quation f(t) = 5 admet une solution unique.
La calculatrice donne a ~1,02.
On admet que l’�quation f (t) = 5 admet une unique solution sur l’intervalle [2; 10], not�e
β, et qu’une valeur approch�e de β � 10 −2 pr�s est 3,46.
b. On consid�re que ce traitement est efficace lorsque la quantit� de m�dicament pr�sente
dans le sang du patient est sup�rieure ou �gale � 5 mg.
D�terminer, � la minute pr�s, la dur�e d’efficacit� du m�dicament dans le cas de ce protocole.
t appartient � [ a ; �] soit t = 3,46 -1,02 = 3,44 h ou 3 h et 26 minutes.
Partie B : �tude du deuxi�me protocole
Le deuxi�me protocole consiste � injecter initialement au patient, par piq�re intraveineuse, une dose
de 2 mg de m�dicament puis � r�injecter toutes les heures une dose de 1,8 mg.
On suppose que le m�dicament se diffuse instantan�ment dans le sang et qu’il est ensuite progressivement �limin�.
On estime que lorsqu’une heure s’est �coul�e apr�s une injection, la quantit� de m�dicament dans le
sang a diminu� de 30 % par rapport � la quantit� pr�sente imm�diatement apr�s cette injection.
On mod�lise cette situation � l’aide de la suite (u n)
o�, pour tout entier naturel n, un d�signe la quantit� de m�dicament,
exprim�e en mg, pr�sente dans le sang du patient imm�diatement apr�s
l’injection de la n-i�me heure. On a donc u 0 = 2.
1. Calculer, selon cette mod�lisation, la quantit� u 1, de m�dicament (en mg) pr�sente dans le sang
du patient imm�diatement apr�s l’injection de la premi�re heure.
u 1 = 0,7 u 0+1,8 =0,7 x 2 +1,8 =3,2 mg.
2. Justifier que, pour tout entier naturel n, on a : u n+1 = 0,7u n +1,8.
u n : quantit� de m�dicament dans le sang � la n-i�me heure.
Une heure plus tard, il reste 0,7 u n mg de m�dicament dans le sang.
Enfin on injecte 1,8 mg de m�dicament dans le sang.
3. a. Montrer par r�currence que, pour tout entier naturel n, on a : u n < u n+1 < 6.
Initialisation : u 1 = 3,2 et u 0 = 2. La propri�t� est vraie au rang 1.
H�r�dit� : un < un+1 < 6 est suppos�e vraie.
0,7 un < 0,7 un+1 < 6x 0,7 = 4,2.
0,7 un+1,8 < 0,7 un+1 +1,8 <4,2 +1,8 = 6.
un+1 < un+2 < 6. La propri�t� est vraie au rang n+1.
Conclusion : la propri�t� est vraie au rang 1 et h�r�ditaire, elle est donc vraie pour tout entier naturel n.
b. En d�duire que la suite (u n) est convergente.
La suite est croissante et major�e par 6, donc d'apr�s le th�or�me de convergence monotone, elle converge.
On note ℓ sa limite.
c. D�terminer la valeur de ℓ. Interpr�ter cette valeur dans le contexte de l’exercice.
A la limite : u n =u n+1= l ; l = 0,7 l +1,8 ; l =6.
4. On consid�re la suite (v n) d�finie, pour tout entier naturel n, par v n = 6−u n.
a. Montrer que la suite (vn) est une suite g�om�trique de raison 0,7 dont on pr�cisera le
premier terme.
v n+1 = 6-u n+1.
v n+1 = 6- 0,7un -1,8= 4,2 -0,7 un = 0,7(6-un) =0,6 vn.
La suite (vn) est g�om�trique de raison q = 0,7 et de premier terme v0 = 6-u0 = 4.
b. D�terminer l’expression de v n en fonction de n, puis de u n en fonction de n.
v n = 4 x0,7 n ; u n = 6-v n = 6- 4 x0,7n.
c. Avec ce protocole, on arr�te les injections lorsque la quantit� de m�dicament pr�sente
dans le sang du patient est sup�rieure ou �gale � 5,5 mg.
D�terminer, en d�taillant les calculs, le nombre d’injections r�alis�es en appliquant ce
protocole.
6-4 x0,7n > 5,5 ; 0,5 > 4 x0,7n ; 0,5 / 4 = 0,125 > 0,7n ;
ln(0,125) > n ln(0,7).
n > ln(0,125) / ln (0,7) ; n > 6 heures.
Soit un total de 7 injections.
QCM.
1. La courbe repr�sentative de la fonction f d�finie sur R par f (x) =
(−2x
2 +3x −1
) / (x
2 +1)
admet pour
asymptote la droite d’�quation :
a. x = −2 ; b. y = −1 ;
c. y = −2 ; d. y = 0
2.
Mettre x2 en facteur commun et simplifier :
f(x) = (-2 +3/x-1/x 2) /(1+1/x 2).
Quand x tend vers plus l'infini, 1 /x et 1 /x 2 tendent vers z�ro. Par suite f(x) tend vers -2.
La droite d'�quation y =-2 est asymptote � la courbe repr�sentant la fonction f.
Soit f la fonction d�finie sur R par f (x) = x exp(
x
2)
.
La primitive F de f sur R qui v�rifie F(0) = 1 est d�finie par :
a. F(x) =
0,5x
2 exp(x 2)
; b. F(x) =
0,5 exp(x2)
;
c. F(x) =(
1+2x
2 ) exp(x2)
; d. F(x) = 0,5 +
0,5 exp(x2) .
F(0) = 1, donc les propositions a et b ne conviennent pas.
On d�rive F(x) =(
1+2x
2 ) exp(x2)
en posant u = 1+2x
2 et v = exp(x2).
u' = 4x ; v' = 2x exp(x2).
u'v +v'u = exp(x2) (4x+2x(1+2x2), diff�re de f(x).
On d�rive F(x) =0,5+0,5 exp(x2) ; F '(x) =0,5 *2x exp(x2) = x exp(x2) = f(x)
3.
On donne ci-contre la repr�sentation
graphique Cf
′ de la fonction d�riv�e
f
′ d’une fonction f d�finie sur R.
On peut affirmer que la fonction f
est :
a. concave sur ]0 ; +∞[ ;
b. convexe sur ]0 ; +∞[ ;
c. convexe sur [0; 2] ;
d. convexe sur [2 ; +∞[.
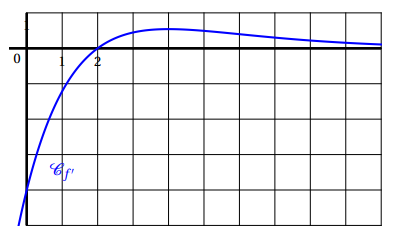
f ' est croissante si x appartient � ] -oo ; 3 ] et d�croissante sur [3 : +oo[.
f " est donc positive sur ] -oo ; 3 ] et n�gative sur [3 : +oo[.
f est convexe sur ] -oo ; 3 ] donc sur [0 ; 2].
4. Parmi les primitives de la fonction f d�finie sur R par f (x) = 3exp(−x
2)
+2 :
a. toutes sont croissantes sur R ; b. toutes sont d�croissantes sur R ;
c. certaines sont croissantes sur R et d’autres
d�croissantes sur R ;
d. toutes sont croissantes sur ] − ∞ ; 0] et
d�croissantes sur [0 ; +∞[.
f(x) est positive sur R ; les primitives de la fonction f , ont pour d�riv�e f.
Donc les fonctions primitives sont croissantes sur R.
5. La limite en +∞ de la fonction f d�finie sur l’intervalle ]0 ; +∞[ par f (x) =
2lnx
/ (x
2 +1)
est �gale � :
a.
2 /
3
; b. +∞ ; c. −∞ ; d. 0.
f(x) = ln (x 2 )/ (x 2+1). Mettre x 2 en facteur commun est simplifier :
f(x) =[ln(x 2 / x 2 ] / (1+1/x 2).
En plus l'infini, par croissance compar�e ln(x2 / x2 ] tend vers z�ro et 1 /x2 tend vers z�ro.
6. L’�quation e 2x +e
x −12 = 0 admet dans R :
a. trois solutions ; b. deux solutions ; c. une seule solution ;
d. aucune solution.
On pose X = ex >0.
X2 +X=12=0.
Discriminant D =12 -4(-12) = 49 = 72.
On retient la solution positive X1 =(-1+7) / 2 = 3 soit x = ln(3).
|
...
|
....
|
QCM.
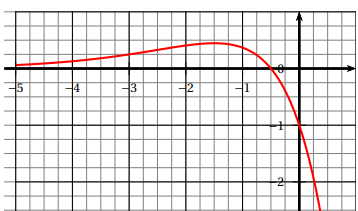
Pour les questions 1 � 3 ci-dessous, on consid�re une fonction f d�finie et deux fois d�rivable sur R.
La courbe de sa fonction d�riv�e f
′
est donn�e ci-dessous.
On admet que f
′
admet un maximum en −
3/
2
et que sa courbe coupe l’axe des abscisses au point de
coordonn�es (-0,5 ; 0).
Question 1 :
a. La fonction f admet un maximum en −
3
/2
;
b. La fonction f admet un maximum en −
1
/ 2
;
c. La fonction f admet un minimum en −
1/
2
;
d. Au point d’abscisse −1, la courbe de la fonction
f admet une tangente horizontale.
f ' est positive sur ]-oo ; -0,5[ ; f(x) est croissante sur cet intervalle.
f ' est n�gative sur ]-0,5 ; +oo[ ; f(x) est d�croissante sur cet intervalle.
f ' s'annule en x = -0,5 ; f(x) admet un maximum.
Question 2 :
a. La fonction f est convexe sur ]
−∞ ; −
3/
2 [
; b. La fonction f est convexe sur �
]−∞ ; −
1/
2[
;
c. La courbe Cf repr�sentant la fonction f n’admet pas de point d’inflexion ;
d. La fonction f est concave sur ]
−∞ ; −
1
/2 |
.
f ' est croissante sur ]
−∞ ; −
3/
2 [
et d�croissante sur ]-3 / 2 ; +oo[.
Donc f " est positive sur ]
−∞ ; −
3/
2 [
et n�gative sur ]-3 / 2 ; +oo[.
f est convexe sur ]
−∞ ; −
3/
2 [.
Question 3 :
La d�riv�e seconde f
′′ de la fonction f v�rifie :
a. f
′′(x) > 0 pour x ∈ ]
−∞ ; −
1/
2 [
; b. f
′′(x) > 0 pour x ∈ [−2 ; −1] ; c. f
′′ (−
3/
2)
= 0 ; d. f
′′(−3) = 0.
f '(x)admet un maximum en x = -3/ 2; donc f " est nulle en x = -3 / 2.
Question 4 :
On consid�re trois suites (un), (vn) et(wn). On sait que, pour tout entier naturel n, on a : un < vn < wn
et de plus :
la limite en plus l'infini de un est �gale � 1 ;
la limite en plus l'infini de wn est �gale � 3.
.
On peut alors affirmer que :
a. la suite (vn) converge ; b. Si la suite (un) est croissante alors la suite
(vn) est minor�e par u0 ;
c. 1 < v0 < 3; d. la suite (vn) diverge.
Si (un) est croissante, pour tout entier naturel, u0 < un < vn.
Donc la suite (vn) est minor�e par u0.
Question 5 :
On consid�re une suite (un) telle que, pour tout entier naturel n non nul : un < un+1 <
1 /
n
.
On peut alors affirmer que :
a. la suite (un) diverge; b. la suite (un) converge;
c. la limite en +oo de (un) est nulle ;
d. la limite en +oo de (un) est �gale � 1.
La suite est croissante.
Pour n diff�rent de z�ro : un < un+1 <
1 /
n
< 1.
La suite est croissante et major�e par 1, donc elle converge.
Question 6 :
On consid�re (un) une suite r�elle telle que pour tout entier naturel n, on a : n < un < n +1.
On peut affirmer que :
a. Il existe un entier naturel N tel que uN est un
entier ;
b. la suite (un) est croissante ;
c. la suite (un) est convergente; d. La suite (un) n’a pas de limite.
Au rang n, on a : n < un < n +1.
Au rang n+1, on a : n+1 < un+1 < un+2.
Donc un < n+1 < un+1 : la suite est croissante.
.
Etude de deux fonctions.
Partie A :
On consid�re les deux fonctions f et g d�finies sur l’intervalle [0 ; +∞[ par :
f (x) = 0,06(
−x
2 +13,7x )
et g(x) = (−0,15x +2,2)e0,2x −2,2.
On admet que les fonctions f et g sont d�rivables et on note f
′
et g
′
leurs fonctions d�riv�es respectives.
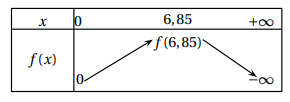
1. On donne le tableau de variations complet de la fonction f sur l’intervalle [0 ; +∞[.
a. Justifier la limite de f en +∞.
f (x) = 0,06x2(
−1 +13,7 / x )
En plus l'infini : 13,7 / x tend vers z�ro.
-1+13,7 /x tend vers -1 et x2 tend vers plus l'infini.
Par produit des limites, f(x) tyend vers moins l'infini.
-x2 tend vers moins l'infini si x tend vers plus l'infini.
b. Justifier les variations de la fonction f .
f '(x) = 0,06 (-2x+13,7).
Si x < 13,7 / 2=6,85, f '(x) est positive et f(x) est croissante.
Si x >6,85, f '(x) est n�gative et f(x) est d�croissante.
Si x = 6,85, f '(x) = 0 et f(x) pr�sente un maximum.
c. R�soudre l’�quation f (x) = 0.
−x
2 +13,7x = x(-x+13,7) = 0
x =0 et x = 13,7.
2. a. D�terminer la limite de g en +∞.
e0,2x tend vers plus l'infini ; −0,15x +2,2 tend vers moins l'infini.
Par produit des limites, g(x) tend vers moins l'infini.
b. D�montrer que, pour tout r�el x appartenant � [0 ; +∞[ on a : g
′
(x) = (−0,03x +0,29)e0,2x
.
On pose u =−0,15x +2,2 et v =e0,2x
.
u' = -0,15 ; v' = 0,2 e0,2x
.
u'v+v'u = e0,2x (-0,15 +0,2(-0,15x+2,2) =e0,2x(-0,03x+0,29).
c. �tudier les variations de la fonction g et dresser son tableau de variations sur [0 ; +∞[.
Pr�ciser une valeur approch�e � 10−2 pr�s du maximum de g.
e0,2x >0. g'(x) a le signe de -0,03x +0,29.
Si x appartient � [0 ; 29 /3[, g'(x) est positive et g(x) est croissante.
Si x > 29 /3 , g'(x) est n�gative et g(x) est d�croissante.
Si x = 29 /3, g('x) =0 et g(x) pr�sente un maximum.
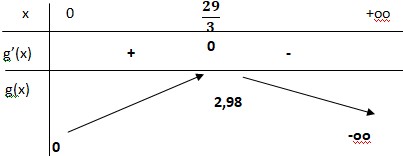
d. Montrer que l’�quation g(x) = 0 admet une unique solution non nulle et d�terminer, �
10−2 pr�s, une valeur approch�e de cette solution.
Sur [0 ; 29 /3], g(x) cro�t de z�ro � 2,98.
Sur [29 /3 , +oo[ :
g(x) d�cro�t de 2,98 � moins l'infini.
g(x) est continue car d�rivable.
Z�ro appartient � ]-oo ; 2,98], dapr�s le th�or�me des valeurs interm�diaires, il existe un r�el unique a tel que g(a) =0.
a = 13,72.
Partie B : trajectoires d’une balle de golf.
Pour frapper la balle, un joueur de golf utilise un instrument
appel� � club � de golf.
On souhaite exploiter les fonctions f et g �tudi�es en Partie A pour
mod�liser de deux fa�ons diff�rentes la trajectoire d’une balle de
golf. On suppose que le terrain est parfaitement plat.
On admettra ici que 13,7 est la valeur qui annule la fonction f et une
approximation de la valeur qui
annule la fonction g.
On donne ci-dessous les repr�sentations graphiques de f et g sur
l’intervalle [0; 13,7]].
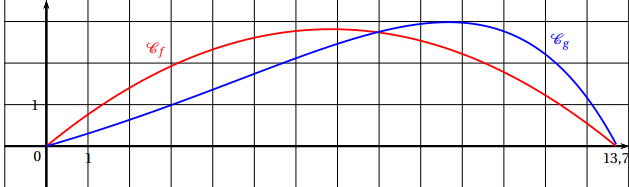
Pour x repr�sentant la distance horizontale parcourue par la
balle en dizaine de yards apr�s la frappe,
(avec 0 < x < 13,7), f (x) (ou g(x) selon le mod�le) repr�sente
la hauteur correspondante de la balle
par rapport au sol, en dizaine de yards (1 yard correspond � environ
0,914 m�tre).
On appelle � angle de d�collage � de la balle, l’angle entre l’axe des
abscisses et la tangente � la courbe
(Cf ou Cg selon le mod�le) en son point d’abscisse 0. Une mesure de
l’angle de d�collage de la balle
est un nombre r�el d tel que tan(d) est �gal au coefficient directeur
de cette tangente.
De m�me, on appelle � angle d’atterrissage � de la balle, l’angle entre
l’axe des abscisses et la tangente
� la courbe (Cf ou Cg selon le mod�le) en son point d’abscisse 13,7.
Une mesure de l’angle d’atterrissage de la balle est un nombre r�el a
tel que tan(a) est �gal � l’oppos� du coefficient directeur de
cette tangente.
Tous les angles sont mesur�s en degr�.
Le sch�ma illustre les angles de d�collage et d’atterrissage associ�s �
la
courbe Cf
Le sch�ma illustre les angles de d�collage et d’atterrissage
associ�s � la courbe Cg .
Premi�re mod�lisation :
on rappelle qu’ici, l’unit� �tant la dizaine de yards, x repr�sente la
distance horizontale parcourue par la balle apr�s la frappe et f (x) la
hauteur correspondante de
la balle.
Selon ce mod�le :
a. Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
Cf : f(6,85) ~2,815 soit 28,15 yards.
b. V�rifier que f
′
(0) = 0,822.
f '(x) = 0,06 (-2x+13,7).
f '(0) = 0,06 *13,7=0,822.
c. Donner une mesure en degr� de l’angle de d�collage de la balle, arrondie au dixi�me.
tan d = f '(0) =0,822 ; d =39,4 �.
d. Quelle propri�t� graphique de la courbe Cf permet de justifier que les angles de d�collage
et d’atterrissage de la balle sont �gaux ?
La trajectoire parabolique est sym�trique par rapport � la droite d'�quation x = 6,85.
2. Seconde mod�lisation :
on rappelle qu’ici, l’unit� �tant la dizaine de yards, x repr�sente la
distance horizontale parcourue par la balle apr�s la frappe et g(x) la
hauteur correspondante de
la balle.
Selon ce mod�le :
a. Quelle est la hauteur maximale, en yard, atteinte par la balle au cours de sa trajectoire ?
On pr�cise que g
′
(0) = 0,29 et g
′
(13,7) ≈ −1,87.
Le maximum de la fonction g(x) est 2,98 soit 29,8 yards.
b. Donner une mesure en degr� de l’angle de d�collage de la balle, arrondie au dixi�me.
tan d = g '(0) =0,29 ; d =16,2 �.
.
c. Justifier que 62 est une valeur approch�e, arrondie � l’unit� pr�s, d’une mesure en degr�
de l’angle d’atterrissage de la balle.
tan a = g'(13,7) = -1,87 ; a ~62�
Partie C : interrogation des mod�les.
� partir d’un grand nombre d’observations des performances de joueurs professionnels, on a obtenu
les r�sultats moyens suivants :
Angle de d�collage en
degr� : 24 ;
Hauteur maximale en yard : 32.
Angle d’atterrissage en
degr�
: 52 .
Distance horizontale en
yard au point de chute : 137.
Quel mod�le, parmi les deux �tudi�s pr�c�demment, semble le plus adapt� pour d�crire la frappe de
la balle par un joueur professionnel ? La r�ponse sera justifi�e.
La distance horizontale est bien confirm�e par les mod�les.
L'angle de d�collage est surestim� ( mod�le 1) et sous-estim� ( mod�le 2).
La hauteur maximale est sous-estim�e par les 2 mod�les.
L'angle de d'atterrissage est surestim� ( mod�le 2) et sous-estim� ( mod�le 1).
Ces mod�les ne sont pas satisfaisant.
|
|
