Mathématiques, probabilités, Bac Métropole 9 /9 / 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Sujet 1. 7 points.
Un hôtel situé à proximité d’un site touristique dédié à la préhistoire propose deux visites
dans les environs, celle d’un musée et celle d’une grotte.
Une étude a montré que 70 % des clients de l’hôtel visitent le musée. De plus, parmi les
clients visitant le musée, 60 % visitent la grotte.
Cette étude montre aussi que 6 % des clients de l’hôtel ne font aucune visite.
On interroge au hasard un client de l’hôtel et on note :
• M l’évènement : « le client visite le musée »;
• G l’évènement : « le client visite la grotte ».
Ainsi, d’après l’énoncé, on a : p(
non M ∩ non G )
= 0,06.
1. a. Vérifier que P non M ( non G) =0,2, probabilité que le client interrogé ne visite pas la grotte sachant
qu’il ne visite pas le musée.
Pnon M ( non G) = P(
non M ∩ non G ) / P(non M) =0,06 / 0,3 =0,2.
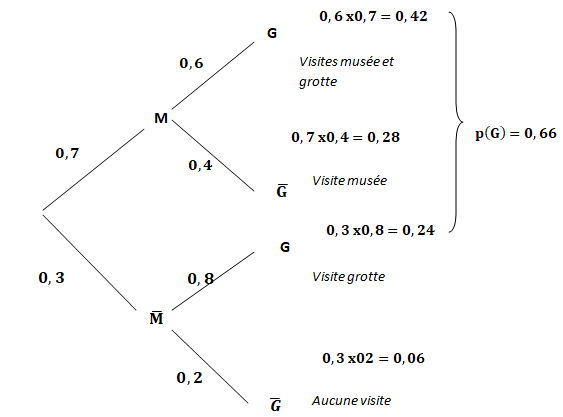
b. L’arbre pondéré suivant modélise
la situation. Recopier et compléter
cet arbre en indiquant sur chaque
branche la probabilité associée.
c. Quelle est la probabilité de l’évènement « le client visite la grotte et ne
visite pas le musée » ? (0,24).
d. Montrer que p(G) = 0,66.
 2.
2. Le responsable de l’hôtel affirme que parmi les clients qui visitent la grotte, plus de la
moitié visitent également le musée. Cette affirmation est-elle exacte ?
P G(M) = P( M ∩ G ) / P(G) =0,42 / 0,66 ~0,63 > 0,5. Affirmation exacte..
3. Les tarifs pour les visites sont les suivants :
• visite du musée : 12 euros;
• visite de la grotte : 5 euros.
On considère la variable aléatoire T qui modélise la somme dépensée par un client de
l’hôtel pour ces visites.
a. Donner la loi de probabilité de T . On présentera les résultats sous la forme d’un
tableau.
T
|
0
|
5
|
12
|
17
|
Probabilité
|
0,06
|
0,24
|
0,28
|
0,42
|
b. Calculer l’espérance mathématique de T .
0 x0,06 +5 x0,24 +12 x0,28 +17 x0,42 =11,7.
c. Pour des questions de rentabilité, le responsable de l’hôtel estime que le montant
moyen des recettes des visites doit être supérieur à 700 euros par jour.
Déterminer le nombre moyen de clients par journée permettant d’atteindre cet
objectif.
700 / 11,7 ~ 60.
4. Pour augmenter les
recettes, le responsable souhaite que l’espérance de la variable
aléatoire modélisant la somme dépensée par un client de l’hôtel pour
ces visites passe
à 15 euros, sans modifier le prix de visite du musée qui demeure à 12
euros.
Quel prix faut-il fixer pour la visite de la grotte afin d’atteindre
cet objectif ? (On admettra que l’augmentation du prix d’entrée de la
grotte ne modifie pas la fréquentation des
deux sites).
.
T
|
0
|
X
|
12
|
12+X
|
Probabilité
|
0,06
|
0,24
|
0,28
|
0,42
|
0 *0,06 +0,24 X +12 *0,28 +(12+X) *0,42 =15.
0,24X +0,42 X= 15-8,4 =4,5 ; X= 10 €.
5. On choisit au hasard 100 clients de l’hôtel, en assimilant ce choix à un tirage avec remise.
Quelle est la probabilité qu’au moins les trois quarts de ces clients aient visité la grotte
à l’occasion de leur séjour à l’hôtel ?
On donnera une valeur du résultat à 10 −3 près.
La probabilité qu'un client visite la grotte est 0,66.
La variable aléatoire Y égale au nombre de visite de la grotte suit la loi binomialeB(100 ; 0,66).
P(Y > 75) ~0,980 d'après la calculatrice.
|
...
|
....
|
Sujet 2. 7 points.
Dans le magasin d’Hugo, les clients peuvent louer deux types de vélos : vélos de route ou
bien vélos tout terrain.
Chaque type de vélo peut être loué dans sa version électrique ou non.
On choisit un client du magasin au hasard, et on admet que :
Si le client loue un vélo de route, la probabilité que ce soit un vélo électrique est de 0,4 ;
Si le client loue un vélo tout terrain, la probabilité que ce soit un vélo électrique est de
0,7 ;
La probabilité que le client loue un vélo électrique est de 0,58.
On appelle x la probabilité que le client loue un vélo de route, avec 0 < x < 1.
On considère les évènements suivants :
• R : « le client loue un vélo de route »;
• E : « le client loue un vélo électrique ».
On modélise cette situation aléatoire à l’aide
de l’arbre reproduit ci-dessous.
1. Recopier cet arbre sur la copie et le compléter.
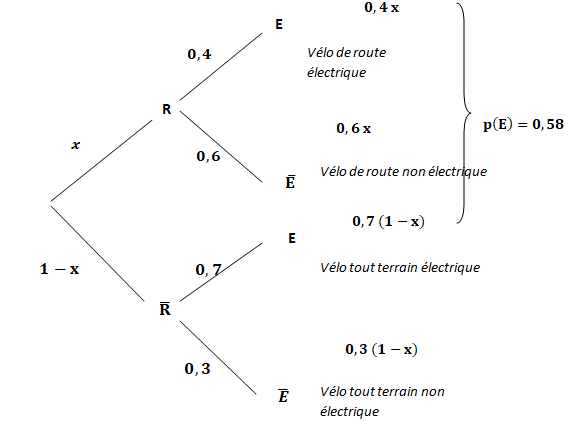
2. a. Montrer que p(E) = 0,7−0,3x.
p(E) = 0,4 x +0,7(1-x) = 0,7−0,3x.
b. En déduire que : x = 0,4.
0,7−0,3x =0,58 ; x = (0,7-0,58) / 0,3 = 0,4.
3. On sait que le
client a loué un vélo électrique. Déterminer la probabilité qu’il ait
loué un vélo tout terrain. On donnera le résultat
arrondi au centième.
PE(non R) =P( E ∩ non R ) / P(E) = 0,7 x(1-0,4) / 0,58 ~0,72.
4. Quelle est la probabilité que le client loue un vélo tout terrain électrique ?
P( E ∩ non R )=0,7 x(1-0,4) = 0,42.
5. Le prix de la location à la journée d’un vélo de route non électrique est de 25 euros,
celui d’un vélo tout terrain non électrique de 35 euros.
Pour chaque type de vélo, le choix de la version électrique augmente le prix de location
à la journée de 15 euros.
On appelle X la variable aléatoire modélisant le prix de location d’un vélo à la journée.
a. Donner la loi de probabilité de X. On présentera les résultats sous forme d’un
tableau.
T
|
25
|
35
|
25+15=40
|
35+15=50
|
Probabilité
|
0,4 x0,6 =0,24
|
0,6 x0,3 =0,18
|
0,4 x 0,4 = 0,16
|
0,6 x 0,7 = 0,42
|
b. Calculer l’espérance mathématique de X et interpréter ce résultat.
25 x0,24 +35 x0,18 +40 x0,16 +50 x 0,42 =6 +6,3 +6,4 +21=39,7.
Une location revient à 39,7 € en moyenne.
6. Lorsqu’on choisit 30
clients d’Hugo au hasard, on assimile ce choix à un tirage avec
remise.
On note Y la variable aléatoire associant à un échantillon de 30
clients choisis au hasard le nombre de clients qui louent un vélo
électrique.
On rappelle que la probabilité de l’événement E est : p(E) = 0,58.
a. Justifier que Y suit une loi binomiale dont on précisera les paramètres.
On répète 30 fois des épreuves identiques et indépendantes avec deux issues possibles. La probabilité du succès est 0,58.
Y suit une loi binomiale de paramètres n = 30 et p = 0,58.
b. Déterminer la probabilité qu’un échantillon contienne exactement 20 clients qui
louent un vélo électrique. On donnera le résultat arrondi au millième.
P(Y=20) = (30 20) x0,5820 x(1-0,58) 30-20 ~0,095.
c. Déterminer la probabilité qu’un échantillon contienne au moins 15 clients qui
louent un vélo électrique. On donnera le résultat arrondi au millième.
P(Y > 15) = 1 -P(Y < 14) ~1- 0,1419 ~0,858.
|
|