Deuxième loi de Kepler, base de Frenet, bac SI Métropole 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Les orbites de la Terre et de Mars sont souvent considérées comme circulaires. Ce sont pourtant des ellipses. Dans le référentiel héliocentrique, la valeur de leur vitesse varie le long de l’orbite entre 𝑣𝑚𝑖𝑛 et 𝑣𝑚𝑎𝑥, tout comme la distance Soleil-planète varie entre 𝑅𝑚𝑖𝑛 et 𝑅𝑚𝑎𝑥. Le rayon moyen 𝑅𝑚𝑜𝑦 est défini comme le rayon du cercle approximant au mieux la trajectoire de la planète. La vitesse 𝑣𝑚𝑜𝑦 est défini comme la vitesse de la planète sur cette trajectoire circulaire. Terre Mars Jupiter vmin ( km /s) 29,3 22,0 12,4 vmax ( km /s) 30,3 26,5 13,7 vmoy ( km /s) 29,8 24,1 13,1 Rmin (km) 147 106 207 106 741 106 Rmax (km) 152 106 249 106 816 106 Rmoy (km) 150 106 228 106 778 106 1. À l’aide de la deuxième loi de Kepler, identifier le schéma correct parmi les suivants. Justifier. Pour chaque schéma, on représente la position de la planète au voisinage de son périhélie P (respectivement aphélie A) entre les instants 𝑡1 et 𝑡1 + ∆𝑡 (respectivement 𝑡2 et 𝑡2 + ∆𝑡) ainsi que son vecteur vitesse à cette position dans le référentiel héliocentrique. 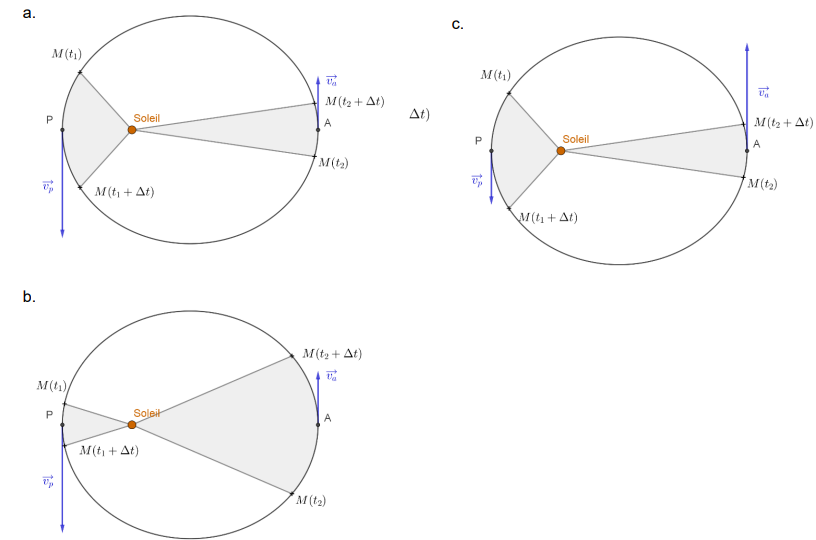b est faux : les aires hachurées parcourues pendant la durée Dt doivent être égales. c est faux : M(t1) M(t1+Dt) > M(t2) M(t2+Dt), donc vP > vA. Lorsque la planète est située à l’aphélie ou au périhélie, le segment Soleil-Terre est perpendiculaire au vecteur vitesse. L’aire balayée par le segment Soleil-Terre pendant une durée ∆𝑡 courte devant la période de révolution, correspond approximativement alors à l’aire du triangle rectangle ayant pour sommets 𝑆, le centre du Soleil, 𝑀(𝑡), position de Terre à l’instant 𝑡 et 𝑀(𝑡 + ∆𝑡), position de Terre à l’instant 𝑡 + ∆𝑡 :  Dans le schéma ci-dessus, 𝑅 est la longueur du segment Soleil-Terre, et 𝑣 × ∆𝑡 la distance parcourue par la planète durant la durée ∆𝑡 à la vitesse 𝑣.  2. Exprimer l’aire balayée par le segment Soleil-Terre durant ∆𝑡 en fonction de 𝑅, 𝑣 et ∆𝑡. Aire du triangle rectangle : Rv Dt / 2. 3. En déterminant la valeur de l’aire balayée par le segment Soleil-Terre durant ∆𝑡 = 1 s, vérifier que les données dans le cas de la Terre sont compatibles avec la seconde loi de Kepler. Rmin Vmax / 2 =149 106 x 30,3 /2 ~2,26 109 km2. Rmax Vmin / 2 =152 106 x 29,3 /2 ~2,23 109 km2. Ecart relatif :( 2,26-2,23 ) / 2,245 ~1,3 inférieur à 2 %, donc résultats compatibles avec la seconde loi de Kepler..  4. À l’aide des données disponibles déterminer si l’aire balayée durant 1 s est la même pour la Terre et pour Mars. Rmin Vmax / 2 = 207 106 x 26,5 /2 ~2,74 109 km2. Ecart relatif :( 2,74-2,26 ) / 2,5 ~0,19 ~ 19 %, donc l’aire balayée durant 1 s est différente pour la Terre et pour Mars. ... .... Pour la suite de l’exercice, on assimilera les orbites à des cercles. On souhaite étudier l’aire balayée en fonction du rayon de l’orbite pendant une même durée. On étudie une planète dont l’orbite est supposée parfaitement circulaire de rayon r. On note M la masse du Soleil. 5. À l’aide de la deuxième loi de Newton, établir l’expression de la vitesse 𝑣 en fonction de 𝐺, r, et 𝑀.  6. Déterminer l’expression de l’aire balayée durant ∆𝑡 en fonction de 𝐺, r, 𝑀 et ∆𝑡. Aire du disque : p r2 pour une circonférence égale à 2 pr. L'aire hachurée correspond à l'arc de cercle v Dt. Aire balayée = r v Dt / 2 = r (GM / r)½ Dt / 2= (rGM)½ Dt / 2.  7. Identifier le graphique correspondant à l’expression de l’aire en fonction de la racine carrée du rayon parmi les propositions suivantes. Justifier. L'aire balayée est proportionnelle à la racine carrée du rayon r. ( le graphe est une droite passant par l'origine).

menu