Pour plus de confort, les voitures sont équipées d’un système de chauffage de l’habitacle.
Dans le cas des véhicules thermiques, c’est la « chaleur » du moteur qui est directement
exploitée. Dans le cas des voitures électriques, le dispositif de chauffage est alimenté par
la batterie. L’utilisation du chauffage diminue donc l’autonomie de la voiture.
Le but de l’exercice est d’étudier l’évolution de la température de l’habitacle d’une voiture
au cours du temps.
Données :
− énergie maximale stockable par la batterie d’une voiture électrique : 40 kWh ;
− autonomie du véhicule à la vitesse fixe de l’étude : 242 km ;
− capacité thermique massique de l’air : 𝑐 = 1,0 kJ⋅K
−1
⋅ kg
−1
;
− volume estimé de l’habitacle : 𝑉 = 2,6 m
3
;
− masse volumique de l’air : 𝜌 = 1,3 kg ⋅ m
−3
;
− surface estimée de l’habitacle : 𝑆 = 8 m
2
.
L’autonomie de la voiture passe de 242 km sans chauffage, à 200 km lorsque le chauffage
est utilisé.
On modélise la situation en considérant que le véhicule évolue à la même vitesse
constante dans les deux cas.
1. Montrer que, dans le cadre de ce modèle, l’énergie 𝐸
chauffage utilisée pour le chauffage
lorsque la voiture roule jusqu’à décharge complète de la batterie est égale à 6,9 kWh.
Le chauffage diminue la distance parcourue de 42 km.
E
chauffage = 40 x42 / 242 ~
6,9 kWh.
2. On choisit comme système l’air contenu dans l’habitacle. On formule les hypothèses
suivantes :
− les transferts thermiques avec l’extérieur ne sont pas pris en compte ;
− l’énergie 𝐸
chauffage est entièrement cédée à l’air contenu dans l’habitacle.
Déterminer la valeur de la variation de température de l’air de l’habitacle. Commenter
la valeur obtenue ainsi que les hypothèses formulées.
Masse d'air contenue dans l'habitacle m = V
r = 2,6 x1,3 =3,38 kg.
E
chauffage = m c
DT ;
DT = Echauffage /( m c) =6,9 103 x3600 /(3,38 x 103) =7,3 103 °C.
Cette valeur est absurde ; il faut prendre en compte les transferts thermiques vers l'extérieur.
On ne chaufe pas que l'air intérieur, mais également les parois internes et le contenu de l'habitacle.
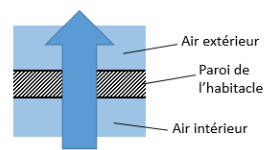
On modélise la carrosserie de l’habitacle par
une paroi uniforme traversée par un flux
thermique. L’air extérieur est à 5°C tandis que
l’air de l’habitacle est à 20°C grâce au
chauffage.
Le sens réel du transfert thermique à travers la
paroi de l’habitacle est représenté par la flèche
verticale . Plus elle est large, plus le transfert
est important.
 3.
3. Justifier le sens du transfert thermique.
Le transfert thermique s'effectue du corps chaud ( l'habitacle) vers le corps froid ( l'air extérieur ).
On s’interroge sur l’influence de la vitesse de la voiture sur la valeur du flux thermique. On
envisage pour cela deux situations :
le cas de la voiture immobile et celui de la voiture en
mouvement.
4. Pour analyser le phénomène en jeu, on propose deux hypothèses, correspondant aux
schémas A et B. Identifier celui qui rend compte de la situation. Justifier sans calcul.
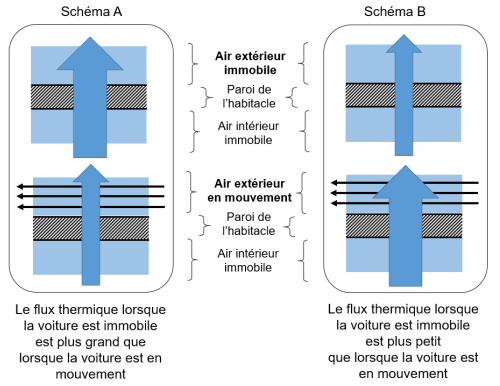
Le schéma B est correct : l'air en mouvement est plus efficace pour prendre de l'énergie à l'habitacle.
On coupe le chauffage. On s’intéresse à l’évolution de la température de l’air 𝑇(𝑡) de
l’habitacle au cours du temps. La température extérieure est supposée constante et notée
𝑇
ext. On note 𝑇
i
la température initiale de l’habitacle.
On suppose que l’équation différentielle suivante modélise l’évolution de la température de
l’habitacle :
𝑑𝑇(𝑡) /
𝑑𝑡 =
1/
𝜏
. (𝑇
ext− 𝑇(𝑡))
5. Déterminer la dimension de la constante 𝜏 en justifiant. Préciser la signification
physique de cette constante et décrire son évolution avec la vitesse du véhicule.
Chaque terme de l'équation est homogène à une température divisée par une durée.
t est homogène à un temps.
t =
(𝑇ext− 𝑇(𝑡)) / [𝑑𝑇(𝑡) /
𝑑𝑡].
A vitesse élevée, l'habitacle se refroidit plus rapidement : t est alors plus faible.