Mathématiques, logarithme, exponentielle, Bac Métropole 9 /9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. 7 points. Partie A.  On considère la fonction f définie sur l’intervalle [1 ; +∞[ par f (x) = ln(x) / x , où ln désigne la fonction logarithme népérien. 1. Donner la limite de la fonction f en +∞. 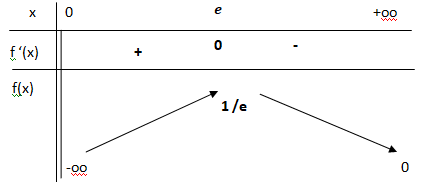Par croissance comparée ln(x) / x tend vers zéro. L'axe des abscisses est asymptote à la courbe représentant f(x). 2. On admet que la fonction f est dérivable sur l’intervalle [1 ; +∞[ et on note f ′ sa fonction dérivée. a. Montrer que, pour tout nombre réel x > 1, f ′ (x) = (1−ln(x)) / x 2 . On pose u = ln(x) et v = x ; u' = 1 /x ; v' = 1. (u'v-v'u) / v2 =(1-ln(x)) / x2.  b. Justifier le tableau de signes suivant, donnant le signe de f ′ (x) suivant les valeurs de x. Le signe de f '(x) est celui de 1-ln(x). Si x < e, 1-ln(x) est positif ; si x > e, 1-ln(x) est négatif. Si x = e, f '(x) est nul. c. Dresser le tableau de variations complet de la fonction f .  3. Soit k un nombre réel positif ou nul. a. Montrer que, si 0 < k < 1 /e , l’équation f (x) = k admet une unique solution sur l’intervalle [1 ; e]. Sur ]0 ; 1 / e], f(x) est strictement croissante de moins l'infini à 1 / e : d'après le théorème des valeurs intermédiaires l'équation f(x) = k admet une solution unique sur cet intervalle.  b. Si k > 1/ e , l’équation f (x) = k admet-elle des solutions sur l’intervalle [1 ; +∞[ ? Justifier. . f(x) < 1 /e : l'équation f(x) = k avec k > 1/e n'admet pas de solution . Partie B.  Soit g la fonction définie sur R par : g(x) = e x /4 . On considère la suite (un) définie par u0 = 1 et, pour tout entier naturel n : un+1 = exp ( un/ 4) c’est-à-dire : un+1 = g (un). 1. Justifier que la fonction g est croissante sur R. g '(x) = 0,25e x /4 > 0. g(x) est strictement croissante sur R.  2. Montrer par récurrence que, pour tout entier naturel n, on a : un < un+1 < e. Initialisation : u0 = 1 ; u1 = e1/4. la propriété est vraie au rang zéro. Hérédité : un < un+1 < e est supposé vrai. La fonction g étant strictement croissante : g( un ) < g(un+1 )< g(e). un+1 < un+2 < g(e). Or g(e) = ee/4~1,9  < e. un+1 < un+2 < e. Conclusion : la prorpiété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n. 3. En déduire que la suite (un) est convergente. La suite est croissante et majorée par e : donc elle converge vers une limite inférieure ou égale à e.  On note ℓ la limite de la suite (un) et on admet que ℓ est solution de l’équation : e x/ 4 = x.  4. En déduire que ℓ est solution de l’équation f (x) = 1 /4 , où f est la fonction étudiée dans la partie A.  La fonction logarithme népérien étant croissante  : e x/ 4 = x conduit à x /4 = ln(x) ; 1 / 4 = ln(x) / x ; f(x) = 1 /4. 5. Donner une valeur approchée à 10−2 près de la limite ℓ de la suite (un). 1 /e ~0,367 ; 1 / 4 = 0,25. L'équation f(x) = 0,25 admet une solution unique sur [1 ; e]. f(1) = 0 ; f(2) = ln(2) / 2 ~0,346. f(1,40) ~0,24 ; f(1,50)~0,27. Donc la limite est comprise entre 1,4 et 1,5. f(1,42 = 0,247 : f(1,43) ~ 0,251. f(1,429) ~0,2498 ; f(1,430) ~0,2501. La limite est égale à environ 1,43. ... .... Sujet 2. 7 points.   Les parties B et C sont indépendantes. Partie A.  On considère la fonction f définie sur ]0 ; +∞[ par f (x) = x − x ln(x), où ln désigne la fonction logarithme népérien. 1. Déterminer la limite de f (x) quand x tend vers 0. ln(x) tend vers moins l'infini ; x ln(x) tend vers zéro et f(x) tend vers zéro. 2. Déterminer la limite de f (x) quand x tend vers +∞. f(x) = x(1-ln(x). ln(x) tend vers plus l'infini ; 1-ln(x) tend vers moins l'infini etpar produit des limites f(x) tend vers moins l'infini. 3. On admet que la fonction f est dérivable sur ]0 ; +∞[ et on note f ′ sa fonction dérivée.  a. Démontrer que, pour tout réel x > 0, on a : f ′ (x) = −lnx. On pose u = x et v = ln(x) ; u' =1 ; v' = 1 /x. u'v+v'u = ln(x)+1 ;  f '(x) = 1-(ln(x) +1) = -ln(x). b. En déduire les variations de la fonction f sur ]0 ; +∞[ et dresser son tableau de variations.  4. Résoudre l’équation f (x) = x sur ]0 ; +∞[. x = x(1-ln(x) ; 1 = 1-ln(x). ln(x) =0 ; x = 1. Partie B. Dans cette partie, on pourra utiliser avec profit certains résultats de la partie A.  On considère la suite (un) définie par :  u0 = 0,5  ; un+1 = un −un ln(un) pour tout entier naturel n.  Ainsi, pour tout entier naturel n, on a : un+1 = f (un). 1. On rappelle que la fonction f est croissante sur l’intervalle [0,5; 1]. Démontrer par récurrence que, pour tout entier naturel n, on a : 0,5 < un < un+1. Initialisation : u0 = 0,5 ; u1 =0,5(1-ln(0,5) ~0,846. La propriété est vraie au rang zéro. Hérédité : 0,5 < un < un+1 est supposé vrai. La fonction f étant strictement croissante : f(0,5) < f( un ) < f(un+1 ). f(0,5) ~ 0,846 ; 0,846 < un+1 < un+2. 0,5 < un+1 < un+2. Conclusion : la prorpiété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.  1. 2. a. Montrer que la suite (un) est convergente. La suite est croisante et bornée par 1 ; donc d'après le théorème de la convergence monotone, la suite converge.  b. On note ℓ la limite de la suite (un). Déterminer la valeur de ℓ. f(un) = un+1. La fonction étant continue : f(l) = l. Or l'équation f(x) = x admet pour solution x = 1 ; en conséquence l = 1. Partie C.  Pour un nombre réel k quelconque, on considère la fonction fk définie sur ]0 ; +∞[ par : fk (x) = k x − x ln(x). 1. Pour tout nombre réel k, montrer que fk admet un maximum yk atteint en xk = e k−1 . Dérivée de -x ln(x) : ln(x) +1. fk'(x) =k -(ln(x) +1) = k-1 -ln(x). fk'(x) =0 si k-1 = ln(x) soit x = ek-1. Si x appartient à ]0 ; ek-1[, fk'(x) >0 et fk (x) est strictement croissante. Si x appartient à ] ek-1; +oo[, fk'(x) < 0 et fk (x) est strictement décroissante. fk admet un maximum yk atteint en xk = e k−1 .  2. Vérifier que, pour tout nombre réel k, on a : xk = yk. yk =fk(xk) = k xk − xk ln(xk) = k e k−1 -e k−1 ln(e k−1 )=k e k−1 -e k−1 (k-1)= e k−1 .

menu