Probabilit�s,
suites, fonctions, Bac Polyn�sie 30 /08 / 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Probabilit�s (7 points)
Parmi les angines, un quart n�cessite la prise d’antibiotiques, les
autres non.
Afin d’�viter de prescrire inutilement des antibiotiques, les m�decins
disposent d’un test de
diagnostic ayant les caract�ristiques suivantes :
• lorsque l’angine n�cessite la prise d’antibiotiques, le test
est positif dans 90 % des cas ;
• lorsque l’angine ne n�cessite pas la prise d’antibiotiques, le test
est n�gatif dans 95 %
des cas.
Les probabilit�s demand�es dans la suite de l’exercice seront arrondies
� 10 −4 pr�s si n�cessaire.
Partie 1
Un patient atteint d’angine et ayant subi le test est choisi au hasard.
On consid�re les �v�nements suivants :
• A : � le patient est atteint d’une angine n�cessitant la prise
d’antibiotiques �;
• T : � le test est positif � .
1. Calculer P(A ∩T
). On pourra s’appuyer sur un arbre pond�r�.
2. D�montrer que P(T ) =
0,2625.
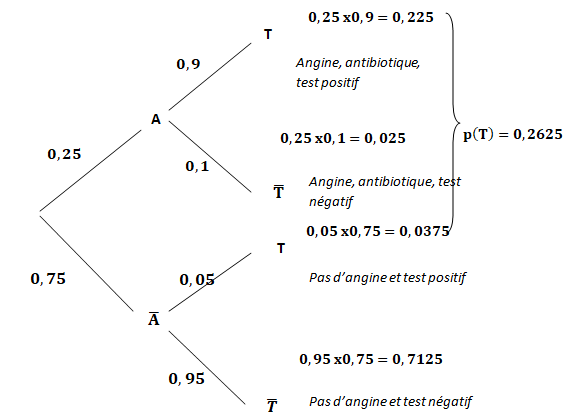3. On choisit un
patient ayant un test positif. Calculer la probabilit� qu’il soit
atteint
d’une angine n�cessitant la prise d’antibiotiques.
P T(A) = P(A ∩T )
/ P(T) =0,225 / 0,2625 ~0,8571.
4. a. Parmi les
�v�nements suivants, d�terminer ceux qui correspondent � un r�sultat
erron� du test :
A ∩T : angine avec antibiotique et test positif, r�sultat
correct.
non A ∩ T : pas dangine et test positif, r�sultat erron�.
A ∩ non T : angine avec antibiotique et test n�gatif, r�sultat erron�.
non A ∩ non T : pas d'angine et test n�gatif, r�sultat correct.
b. On d�finit
l’�v�nement E : � le test fournit un r�sultat erron� �.
D�montrer que p(E) = 0,0625.
P(A ∩
nonT) + P(non A ∩ T)
=0,025 +0,0375 =0,0625.
Partie 2
On s�lectionne au hasard un �chantillon de n patients qui ont �t�
test�s.
On admet que l’on peut assimiler ce choix d’�chantillon � un tirage
avec remise.
On note X la variable al�atoire qui donne le nombre de patients de cet
�chantillon ayant un
test erron�.
1. On suppose que n
= 50.
a. Justifier que la
variable al�atoire X suit une loi binomiale B(n, p) de param�tres
n = 50 et p = 0,0625.
C'est
un sch�ma de bernoulli. : on r�p�te 50 exp�riences al�atoires ayant
deux issues, identiques et ind�pendantes entre elles.
X
suit la loi binomiale de param�tre n = 50 et p =0,0625.
b. Calculer P(X = 7).
P(X=7) =0,0232.
c. Calculer la
probabilit� qu’il y ait au moins un patient dans l’�chantillon dont le
test est erron�.
1-P(X=0) = 1-0,03968 =0,9603.
2. Quelle valeur
minimale de la taille de l’�chantillon faut-il choisir pour que P(X
> 10)
soit sup�rieure � 0,95 ?
P(X > 10) > 0,95.
P(X > 9) > 0,95.
n= 88.
|
...
|
....
|
Suites, fonctions ( 7 points )
Soit k un nombre r�el.
On consid�re la suite (un) d�finie par son premier terme u0 et pour tout entier naturel n,
un+1 = kun (1−un).
Les deux parties de cet exercice sont ind�pendantes.
On y �tudie deux cas de figure selon les valeurs de k.
Partie 1
Dans cette partie, k = 1,9 et u0 = 0,1.
On a donc, pour tout entier naturel n, un+1 = 1,9un (1−un).
On consid�re la fonction f d�finie sur [0; 1] par f (x) = 1,9x(1− x).
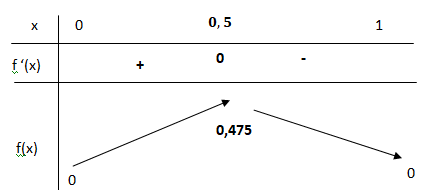
a. �tudier les variations de f sur l’intervalle [0; 1].
On d�rive en posant u = x et v = 1-x ; u' = 1 ; v' = -1.
u'v+v'u = 1-x-x =1-2x.
f '(x) = 0 si x =0,5.
f '(x) < 0 si x appartient � ]0,5 ; 1] et f(x) est d�croissante.
f '(x) > 0 si x appartient � [0 ; 0,5[ et f(x) est croissante.
b. En d�duire que si x ∈ [0 ; 1] alors f (x) ∈ [0 ; 1].
f(0) = 0 ; f(1) = 0 ; f(0,5) =0,475.
2. Ci-dessous sont repr�sent�s les premiers termes de la suite (un) construits � partir de
la courbe Cf de la fonction f et de la droite D d’�quation y = x.
Conjecturer le sens de variation de la suite (un) et sa limite �ventuelle
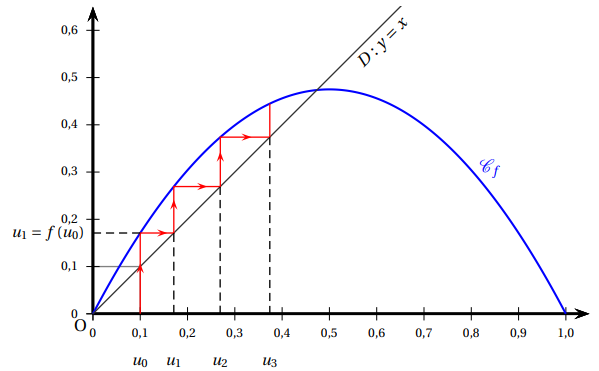
La suite est croissante, tend vers f(0,5)= 0,475.
3. a. En utilisant les r�sultats de la question 1, d�montrer par r�currence que pour tout
entier naturel n :
0 < un < un+1 < 0,5
.
Initialisation : u0 = 0,1 ; u1 = 1,9u0 (1−u0)=1,9 *0,1 (1-0,1)= 0,171.
La propri�t� est vraie au rang z�ro.
H�r�dit� : 0 < un < un+1 < 0,5 est suppos�e vraie.
Sur [0 ; 0,5] la fonction f �tant croissante : f(0) < f(un) < f(un+1) < f(0,5).
0 < un+1 < un+2 < 0,475 < 0,5.
La propri�t� est vraie au rang n+1.
Conclusion : la prori�t� �tant vraie au rang z�ro et h�r�ditaire, elle est donc vraie pour tout entier naturel n.
b. En d�duire que la suite (un) converge.
La suite �tant croissante et born�e, elle converge.
c. D�terminer sa limite.
La suite converge vers f(0,5) = 0,475.
Partie 2.
Dans cette partie, k = 0,5
et u0 = 0,25
.
On a donc, pour tout entier naturel n, un+1 =
0,5un (1−un) et u0 = 0,25
.
On admet que pour tout entier naturel n : 0 < un < 0,5n
.
1. D�montrer que la suite (un) converge et d�terminer sa limite.
un+1-un=0,5un (1−un) -un =0,5un -un-0,5 un2 = - 0,5un -0,5 un2 < 0.
La suite est d�croissante.
0 < un < 0,5n
.
un+1 < 0,5 * 0,5n (1-
0,5n).
Quand n tend vers l'infini, 0,5 n tend vers z�ro.
un+1 tend vers z�ro.
La suite �tant d�croissante et born�e, elle converge.
2. On consid�re la fonction Python algo (p) o� p d�signe un entier naturel non nul :
def algo(p)
u = 0,25
n =0
while u >10**(-p) :
u = 0.5*u(1-u)
n = n+1
return n
Expliquer pourquoi, pour tout entier naturel non nul p, la boucle while ne tourne pas
ind�finiment, ce qui permet � la commande algo (p) de renvoyer une valeur.
Par exemple pour p = 2.
n
|
0
|
1
|
2
|
3
|
4
|
u
|
0,25
|
0,09375
|
0,04248
|
0,02033
|
0,00996
|
u > 10-p
|
vrai
|
vrai
|
vrai
|
vrai
|
faux
|
u est d�croissant et tend vers z�ro.
Exercice 3. Fonction ( 7 points).
Partie 1.
Soit g la fonction d�finie pour tout nombre r�el x de l’intervalle ]0; + ∞[ par :
g(x) =
2ln(x)
/ x
.
1. On note g
′
la d�riv�e de g. D�montrer que pour tout r�el x strictement positif :
g
′
(x) =
(2−2ln(x)) /
x
2
.
On pose u = 2ln(x) et v = x ; u' = 2 /x ; v' = 1.
(u'v-v'u) / v2 = (2 -2ln(x) ) / x2 .
2. On dispose de ce tableau de variations de la fonction g sur l’intervalle ]0 ; +∞[ :
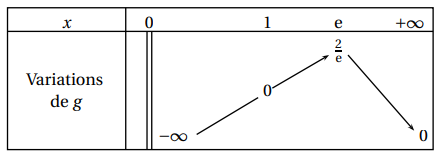
Justifier les informations suivantes lues dans ce tableau :
a. la valeur 2
e.
b. les variations de la fonction g sur son ensemble de d�finition.
g'(x) a le signe de 1-ln(x).
Si 0 < x < e, g'(x) >0 et g(x) est croissante.
Si x > e, g'(x) < 0 et g(x) est d�croissante.
Si x = e, g'(x) =0, g(x) pr�sente un maximum g(e) = 2 ln(e) / e = 2 /e.
c. les limites de la fonction g aux bornes de son ensemble de d�finition.
Quand x tend vers z�ro, ln(x) tend vers moins l'infini et g(x) tend vers moins l'infini.
Quand x tens vers plus l'infini, par croissance compar�e ln(x) / x tend vers 0.
3. En d�duire le tableau de signes de la fonction g sur l’intervalle ]0 ; +∞[.
Quand x appartient � ]0 ; 1[, g(x) < 0 ; quand x appartient � ]1 ; +oo[, g(x) > 0.
Partie 2.
Soit f la fonction d�finie sur l’intervalle ]0; + ∞[ par
f (x) = [ln(x)]2
.
Dans cette partie, chaque �tude est effectu�e sur l’intervalle ]0 ; +∞[.
1. D�montrer que sur l’intervalle ]0 ; +∞[, la fonction f est une primitive de la fonction
g.
u = ln(x) ; u' = 1 /x ; f = u2 ; f '(x) = 2 u u' = 2 ln(x) / x =g(x).
2. � l’aide de la partie 1, �tudier :
a. la convexit� de la fonction f ;
f '(x) =g(x) ; f "(x) = g'(x).
Si 0 < x < e, f "(x) >0 et f(x) est convexe.
Si x > e, f "(x) < 0 et f(x) est concave.
b. les variations de la fonction f.
Quand x appartient � ]0 ; 1[, g(x) < 0 ; f(x) est d�croissante.
Quand x appartient � ]1 ; +oo[, g(x) > 0 ; f(x) est croissante.
Quand x = e; f(x) pr�sente un minimum f(e) = 1.
3. a. Donner une �quation de la tangente � la courbe repr�sentative de la fonction f
au point d’abscisse e.
f '(e)=g(e)=2 /e.
Equation de la tangente : y = 2x / e + cste.
f(e) = 1 ; 1 = 2 +Cste ; Cste = -1.
y = 2x /e-1.
b. En d�duire que, pour tout r�el x dans ]0 ; e] :
[ln(x)]2 >
2x / e −1.
Si 0 < x < e, f "(x) >0 et f(x) est convexe. La courbe repr�sentative de f(x) est au dessus de ces tangentes.
La tangente en x = e a pour �quation y = 2x /e-1.
Donc
[ln(x)]2 >
2x / e −1.
|
|
