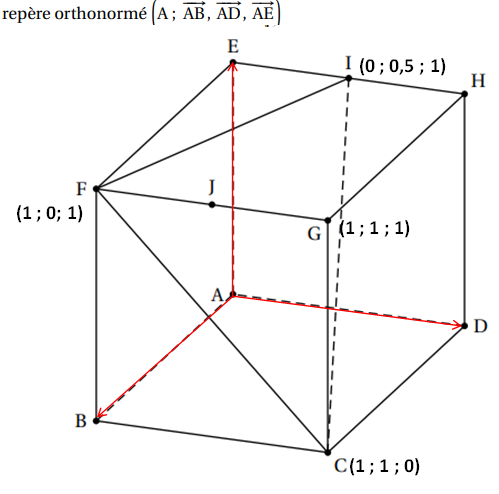
1. a. Donner sans justifier les coordonn�es des points C, F et G.
b. D�montrer que le vecteur n de coordonn�es (1 ; 2 ; 2) est normal au plan (CFI).
On montre que deux vecteurs non colin�aires du plan (CFI) sont orthogonaux au vecteur n.
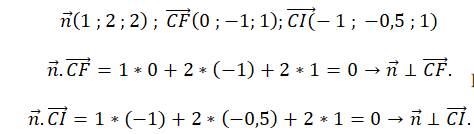c. V�rifier qu’une �quation cart�sienne du plan (CFI) est : x +2y +2z −3 = 0.
Le vecteur n �tant orthogonal au plan (CFI), une �quation cart�sienne de ce plan est :
x+2y+2z+d = 0.
C (1 ; 1 ; 0) appartient � ce plan : 1+2*1+2*0+d = 0 doit d = -3.
2. On note d la droite passant par G et orthogonale au plan (CFI).
a. D�terminer une repr�sentation param�trique de la droite d.
Le vecteur n est un vecteur directeur de la droite d.
x = t+x
G =t+1 ; y = 2t+y
G =
2t+1 ;
z = 2t+zG = 2t+1 avec t r�el.
b. D�montrer que le point K(
7/
9
;
5/
9
;
5/
9 )
est le projet� orthogonal du point G sur le
plan (CFI).
K appartient � la droite d et au plan (CFI) :
t+1 +2(2t+1)+2(2t+1)-3 = 0 ;
9t =2 ; t = -2 / 9.
x
K = -2 / 9+1 = 7 /9 ; y
K = -4 / 9+1 = 5 /9 ; zK = -4 / 9+1 = 5 /9.
c. D�duire des questions pr�c�dentes que la distance du point G au plan (CFI) est
�gale � 2 /
3.
GK =[(7 / 9-1)
2 +
(5 / 9-1)2 +(5 / 9-1)2 ]
� =
[(-2 / 9)2 +(-4 / 9)2 +(-4 / 9)2 ]� =(36 / 81)� =6 / 9 =2 / 3.
3. On consid�re la pyramide GCFI.
On rappelle que le volume V d’une pyramide est donn� par la formule
V =
1
3
�b �h,
o� b est l’aire d’une base et h la hauteur associ�e � cette base.
a. D�montrer que le volume de la pyramide GCFI est �gal � 1/
6
, exprim� en unit� de
volume.
Aire de la base CFG = FG x CG / 2 = 1 x1 / 2 =0,5 unit� d'aire.
Hauteur IJ = 1.
Volume de cette pyramide : 0,5 x1 / 3 = 1 / 6 unit� de volume.
b. En d�duire l’aire du triangle CFI, en unit� d’aire.
Aire du triangle CFI x GK / 3 = 1 / 6 ;
Aire du triangle CFI = 1/ (2 GK) =3 / 4.
