Mathématiques,
suites, fonction, bac Polynésie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
QCM. 7 points.
1. On considère la fonction f définie et dérivable sur ]0 ; +oo[ par f(x) = x ln(x)-x+1.
Parmi les 4 expressions suivantes, laquelle est f '(x) ?
a. ln(x) vrai ; b. 1/x-1 ; c. ln(x)-2 ; d. ln(x) -1.
On pose u = x et v = ln(x) ; u' = 1 ; v' = 1 /x.
u'v+v'u = ln(x)+1
f '(x) = ln(x) +1-1 = ln(x).
2. On considère la fonction g définie sur ]0 ; +∞[ par g(x) = x2
[1−ln(x)].
Parmi les quatre affirmations suivantes, laquelle est correcte ?
a. En 0, limite de g(x) = +oo ; b. En 0, limite de g(x) = -oo ; c. En 0, limite de g(x) = 0 ; vrai
d. La fonction g
n’admet pas de limite en 0
En zéro, ln(x) tend vers -oo ; 1 -ln(x) tend vers +oo ; x2 tend vers zéro ; g(x) tend vers zéro.
3. On considère la fonction f définie sur R par f (x) = x3 − 0,9x2 − 0,1x. Le nombre de
solutions de l’équation f (x) = 0 sur R est :
a. 0 ; b. 1 ; c. 2 ; d. 3. Vrai.
x(x2 − 0,9x − 0,1)=0 ; solution x = 0.
x2 − 0,9x − 0,1 =0 ; discriminant D =0,92 +0,4 >0, donc deux racines réelles.
4. Si H est une primitive d’une fonction h définie et continue sur R, et si k est la fonction
définie sur R par k(x) = h(2x), alors, une primitive K de k est définie sur R par :
a. K (x) = H(2x) ; b. K (x) = 2H(2x) ; c. K (x) = 0,5
H(2x) vrai ; d. K (x) = 2H(x).
Soit K(x) = 0,5 H(2x) ; K' = 0,5 x2H'(2x) = H'(2x)
H'(x) = h(x) car H est une primitive de h.
K'(x) =k(x).
5. L’équation réduite de la tangente au point d’abscisse 1 de la courbe de la fonction f
définie sur R par f (x) = xe
x
est :
a. y = ex +e ; b. y = 2ex −e vrai; c. y = 2ex +e ; d. y = ex.
Calcul de f '(x) en posant u = x, v = ex ; u' = 1 v' = ex.
u'v+v'u = ex+xex.
f '(1) =2e.
Equation de la tangente y = 2e x +b.
Le pont de coordonnées 1 ; f(1) = e appartient à la tangente : e = 2e+b soit b = -e.
Equation de la tangente : y = 2e x-e.
6. Les nombres entiers n solutions de l’inéquation (0,2)n < 0,001 sont tous les nombres
entiers n tels que :
a. n < 4 ; b. n < 5 ; c. n > 4 ; d. n > 5 vrai.
n ln(0,2) < ln(0,001) ; n ln(1 /5) < ln(1 /1000).
-n ln(5) < -ln(1000) ; n ln(5) > ln(1000) ; n >ln(1000) / ln(5) ; n >4,29.
Suite, fonction. (7 points)
Au début de l’année 2021, une colonie d’oiseaux comptait 40 individus. L’observation conduit
à modéliser l’évolution de la population par la suite (un) définie pour tout entier naturel n
par :
u0 = 40;
un+1 = 0,008un (200−un)
où un désigne le nombre d’individus au début de l’année (2021+n).
1. Donner une estimation, selon ce modèle, du nombre d’oiseaux dans la colonie au début de l’année 2022.
u1 = 0,008u0 (200−u0) = 0,008 x40 (200-40)=51,2. Donc 51 oiseaux.
On considère la fonction f définie sur l’intervalle [0; 100] par f (x) = 0,008x(200− x).
2. Résoudre dans l’intervalle [0; 100] l’équation f (x) = x.
0,008x(200− x) = x.
x = 0 est solution .
0,008(200-x) = 1 : 200-x = 125 ; x = 75.
3. a. Démontrer que la fonction f est croissante sur l’intervalle [0; 100] et dresser son
tableau de variations.
On pose u = 0,008x ; v = 200-x ; u' = 0,008 et v' = -1.
f '(x) =0,008(200-x)-0,008x = 1,6 -0,016x = 0,016 ( 100-x).
f '(x) est positive sur cet intervalle et f(x) est croissante de 0 à 80.
b. En remarquant que, pour tout entier naturel n, un+1 = f (un) démontrer par récurrence que, pour tout entier naturel n :
0 < un < un+1 < 100.
Initialisation : u0 = 40 et u1 = 51, la propriété est vraie au rang zéro.
Hérédité : 0 < un < un+1 < 100 est supposée vraie.
f étant croissante : f(0) < f(un) < f(un+1) < f(100).
40 < un+1 < un+2 < 80 < 100.
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire ; elle est vraie pour tout entier n.
c. En déduire que la suite (un) est convergente.
La suite est croissante et majorée par 100, donc elle converge.
d. Déterminer la limite ℓ de la suite (un). Interpréter le résultat dans le contexte de
l’exercice.
un+1 = un = l.
f(l) = l ; 0,008l(200− l)= l..
l = 75.
4. On considère l’algorithme suivant :
def seuil(p) :
n=0
u = 40
while u < p :
n =n+1
u = 0.008*u*(200-u)
return(n+2021)
L’exécution de seuil(100) ne renvoie aucune valeur. Expliquer pourquoi à l’aide de la
question 3.
La limite de la suite est 75, toutes les valeurs de un seront inférieure à 75 et donc à 100,
l’exécution de seuil(100) « tournera » indéfiniment. La boucle while est donc infinie.
|
...
|
....
|
QCM
1. On considère la fonction g définie est dérivable sur ]0 ; +∞[ par :
g(x) = ln(
x
2 + x +1 )
.
Pour tout nombre réel x strictement positif :
a. g
′
(x) =
1/ (
2x +1) ;
b. g
′
(x) =
1
/ (x
2 + x +1).
c. g
′
(x) = ln(2x +1) ; d. g
′
(x) =
(2x +1)/(
x2 + x +1). Vrai
On pose u = x2+x+1 ; u' = 2x+1 ; g'(x) = u' / u =
(2x +1)/(
x2 + x +1).
2. La fonction ln(x) admet pour primitive sur ]0 ; +∞[ la fonction :
a. ln(x) ; b. 1 /x ; c. x ln(x)− x vrai ;d.
ln(x)
/ x
.
On dérive xln(x)-x : u = x ; v = ln(x) ; u' = 1 ; v' = 1 / x ; u'v+v'u =ln(x)+1.
Dérivée de x ln(x) -x = ln(x)+1-1 = ln(x).
3. On considère la suite (an) définie pour tout n dans N par :
an =
(1−3
n) / (
1+2
n)
.
La limite de la suite (an) est égale à :
a. −∞ vrai ; b. −1; c. 1 ; d. +∞.
an = 3n(1 / 3n-1) / [2n(1 / 2n+1)]
Quand n tend vers plus l'infini : 1 / 3n et 1 / 2n tendent vers zéro.
an tend vers -(3 /2)n soit vers moins l'infini.
4. On considère une fonction f définie et dérivable sur [−2 ; 2]. Le tableau de variations
de la fonction f
′ dérivée de la fonction f sur l’intervalle [2 ; 2] est donné par :
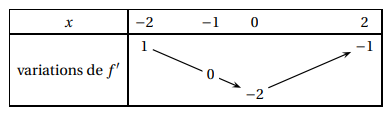
La fonction f est :
a. convexe sur [−2 ; −1] ; b. concave sur [0; 1]
; c. convexe sur [−1 ; 2] d. concave sur [−2 ; 0]. Vrai.
La variation de la dérivée f ' indique :
f ' est décroissante sur [-2 ; 0], donc f est concave sur cet intervalle.
5. On donne ci-dessus la courbe représentative de la dérivée f
′ d’une fonction f définie
sur l’intervalle [−2 ; 4].
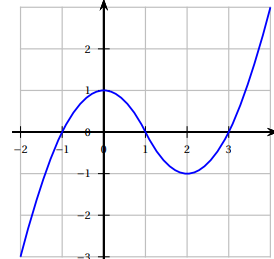
Par lecture graphique de la courbe de f
′
, déterminer l’affirmation correcte pour f :
a. f est décroissante sur [0; 2] ; b. f est décroissante sur [−1 ; 0]
; c. f admet un maximum en 1 sur [0 ; 2] vrai ;
d. f admet un maximum en 3 sur [2; 4].
En 1, f '(x) s'annule ; f(x) présente un extrémum.
f '(x) est positive sur [0 ; 1 ] ; f(x) est croissante.
f '(x) est négative sur [1 ; 2 ] ; f(x) est décroissante.
6. Une action est cotée à 57 €. Sa valeur augmente de 3 % tous les mois.
La fonction python seuil() qui renvoie le nombre de mois à attendre pour que sa valeur
dépasse 200 € est :

La boucle while doit s'excécuter tant que v <200 et il faut
augmenter de 1 le nombre de mois à chaque exécution de la boucle. Réponse a.
Suites.
Soit (un) la suite définie par u0 = 1 et pour tout entier naturel n
un+1 =
un / (
1+un).
1. a. Calculer les termes u1, u2 et u3. On donnera les résultats sous forme de fractions
irréductibles.
u1=1 / 2.
u2=1/2 / (1+1/2)=1 /3.
u2=1/3 / (1+1/3)=1 /4.
b. Recopier le script python ci-dessous et compléter les lignes 3 et 6 pour que liste(k)
prenne en paramètre un entier naturel k et renvoie la liste des premières valeurs
de la suite (un) de u0 à uk.

2. On admet que, pour tout entier naturel n, un est strictement positif.
Déterminer le sens de variation de la suite (un).
un+1 -un=
un / (
1+un) -un =(un-un-un2) / (1+un).= -un2 / (1+un).
un+1 -un < 0, la suite est décroissante.
3. En déduire que la suite (un) converge.
La suite est décroissante et la suite est minorée par zéro. Donc elle converge.
4. Déterminer la valeur de sa limite.
f(x) = x /(1+x) ; la fonction f est continue car dérivable sur R+.
Donc f(l) = l.
l = l / (1+l) ; l2+l=l ; l = 0.
5. a. Conjecturer une expression de un en fonction de n.
un = 1 / (n+1).
b. Démontrer par récurrence la conjecture précédente.
Initialisation : la propriété est vraie au rang 1 : u1 = 1 /2.
Hérédité : la propriété est supposée vraie au rang n.
un = 1 / (n+1).
un+1 =
un / (
1+un) = [1 / (n+1)] / [1+1/(n+1)] =1 / (n+2).
La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang un et héréditaire ; elle est vraie pour tout entier n.
|
|