On
cherche � �tudier la trajectoire du ballon lors du tir au but � partir
de la vid�o de la finale de 1976.
Les informations extraites de la vid�o sont les suivantes :
- le ballon traverse la ligne de but � t
b = 0,96 s ;
- le ballon semble traverser la ligne de but en plein milieu de la cage � la fois dans le sens de
la hauteur et de la largeur.
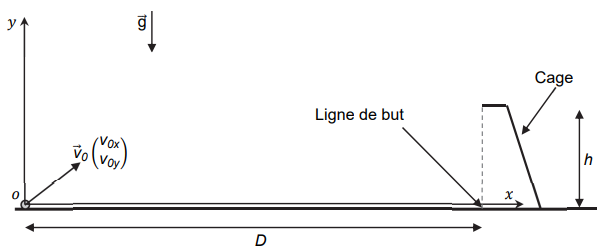
− distance jusqu’� la ligne de but lors d’un tir au but : D = 11 m ;
− dimensions de la cage de but : L = 7,32 m en largeur et h = 2,44 m en hauteur ;
− vitesse initiale moyenne d’un tir au but lors d’un penalty � classique � : 120 km.h
-1 .
Q1. Repr�senter sur un sch�ma le ballon et la ou les force(s) qui s’exercent sur lui entre l’instant
de la frappe et celui de l’impact avec le sol (on n�glige l’influence de l’air).
Le ballon n'est soumis qu'� son poids.
Q2. D�terminer l’expression des coordonn�es du vecteur acc�l�ration dans le rep�re propos�
sur la figure.
Le ballon n'est soumis qu'� son poids.
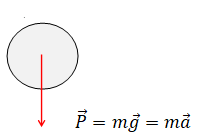
ax = 0 ; ay= -g.
.
Q3. Montrer que les �quations horaires du mouvement sont les suivantes :
x(t) = v
0xt
; y(t) = - 0,5 gt
2 + v
0yt.
La vitesse est une primitive de l'acc�l�ration.
v
x(t) = a
xt +constante = constante = v
0x.
vy(t) = ayt +constante = -gt + constante.
� t = 0, vy(0) = v0y = constante.
vy(t) = ayt +v0y .
La position est une primitive de la vitesse et la position initiale est l'origine du rep�re.
x(t) = v0xt
; y(t) = - 0,5 gt2 + v0yt.
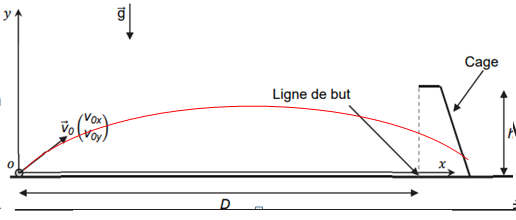
Q4. Recopier le sch�ma de situation et tracer l’allure de la trajectoire du ballon.
Q5. En utilisant les �quations horaires et les donn�es fournies, d�terminer les valeurs de
v0x et
de v
0y.
v0x= D / tb=11 /0,96 =11,46 ~11 m /s.
y(tb) =0,5 h = - 0,5 gtb2 + v0ytb.
voy=(1,22 +0,5 x9,81 x0,962) / 0,96 =5,97 ~6,0 m /s.
Q6. V�rifier que Panenka frappe effectivement � mollement � (c’est-�-dire faiblement) dans le
ballon
v0=120 / 3,6= 33,3 m/s.
v02 = v0x2 +v0y2 =11,462 +5,972 = 166,97 ; vo ~13 m /s ou 13 x3,6 ~47 km /h.
Cette valeur �tant bien inf�rieure � 120 km /h, la frappe est molle.
