Physique chimie, mathématiques,  Bac STI2D Métropole, Antilles 9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Une horloge au jus d'orange. Pour mettre en évidence le principe de fonctionnement d’une pile, il est possible d’alimenter une horloge grâce à une pile rudimentaire constituée d’une électrode de cuivre et d’une électrode en magnésium plongeant dans du jus d’orange. En réalisant l’expérience les valeurs suivantes sont relevées : Durée de fonctionnement maximale Environ 21h.  Tension 1,52 V.  Intensité du courant électrique 0,3mA.  pH du jus d’orange au début et à la fin de l’expérience Début : 3,9 Fin : 6,5.  Volume du jus d’orange 140 mL.  Le but de cet exercice est de modéliser le fonctionnement de cette pile à l’aide d’un modèle mathématique en cohérence avec les résultats expérimentaux mesurés.  Partie A : étude de la pile.  Lorsque cette pile rudimentaire est en fonctionnement, l’électrode en cuivre est le siège d’une transformation chimique modélisée par la demi-équation électronique suivante : 2H+(aq)+2e− →H2(g).  L’électrode en magnésium est quant à elle le siège d’une transformation chimique modélisée par la demi-équation électronique : Mg(s)→Mg2+(aq) +2e−. 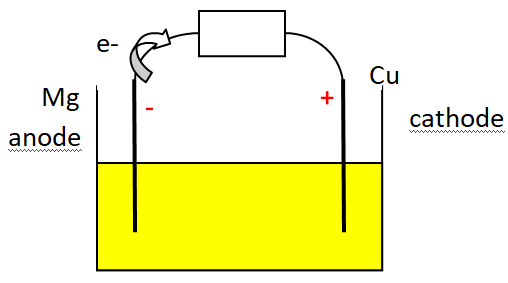1. Schématiser cette pile alimentant un dipôle (modélisant l’horloge) en indiquant le sens de circulation des électrons et en identifiant clairement les deux électrodes. Repérer sur le schéma l’anode et la cathode de cette pile.  2. À partir des deux demi-équations électroniques, écrire l’équation de la réaction qui modélise le fonctionnement de la pile. Mg(s)→Mg2+(aq) +2e−. 2H+(aq)+2e− →H2(g). Addition : Mg(s) +2H+(aq)+2e−→Mg2+(aq) +2e−+ H2(g). Simplifier : Mg(s) +2H+(aq)→Mg2+(aq) + H2(g).  3. Utiliser l’équation de la réaction précédente pour expliquer qualitativement l’évolution du pH du jus d’orange lorsque la pile débite. Les ions H+ sont consommés, leur concentration diminue et le pH augmente.  On désire comparer la durée maximale de fonctionnement obtenue en utilisant la pile au jus d’orange et celle que l’on aurait avec une pile LR6 standard achetée en magasin.  4. Une pile LR6 a une quantité d’électricité stockée moyenne de 2 800 mAh. En admettant que la pile LR6 débite un courant d’intensité identique à celle de la pile à jus d’orange, calculer la durée maximale de fonctionnement de l’horloge alimentée par la pile LR6. En déduire le nombre de piles au jus d’orange nécessaires pour remplacer une pile du commerce. Durée t = Q / I = 2 800 / 0,3 = 9,3 103 heures pour la pile LR6. 9,3 103 / 21 ~ 445 pile au jus d'orange. Partie B : étude mathématique.  On note t le temps, exprimé en minute, écoulé depuis la mise en fonctionnement de la pile au jus d’orange. À l’aide d’une étude expérimentale, la valeur du pH en fonction du temps peut être modélisée par la fonction f définie sur [0 ;+∞[ par : f (t) = 6,571−2,671exp(− t / 261 ). Une représentation graphique de f est donnée ci-dessous. 1. Calculer f (0). Interpréter ce résultat dans le contexte de l’expérience. f(0) = 6,571 -2,671 = 3,9  ( pH initial du jus ). 2. a. Résoudre graphiquement l’équation f (t) = 5. Donner le résultat en heure et minute. 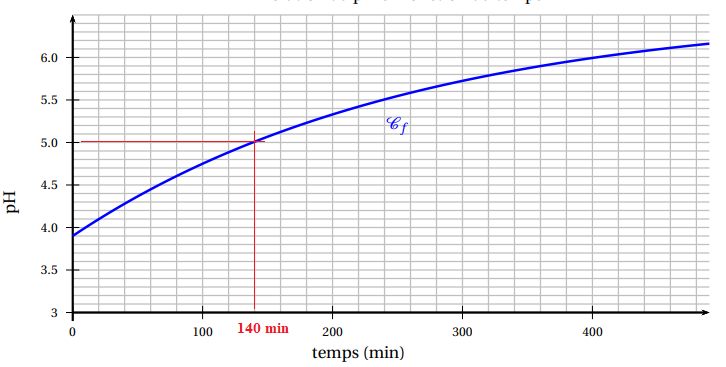140 min = 2 h 20 min.  b. Résoudre algébriquement l’équation f (t) = 5. Donner le résultat arrondi à la minute. Comparer ce résultat à celui obtenu à la question 2. a. 6,571−2,671exp(− t / 261 ) = 5 ; 6,571-5 =1,571= 2,671exp(− t / 261 ). 1,571 / 2,67 =0,588 ; ln(0,588) = -t / 261 ; 0,530 = t / 261 ; t ~138  min, en accord avec le graphe. 3. Calculer lim t→+∞ f (t). Le résultat est-il compatible avec les valeurs relevées lors de l’expérience ? exp(− t / 261 ) tend vers 0 si t tend vers + oo. 2,671exp(− t / 261 ) tend vers 0 si t tend vers + oo. pH tend vers 6,57, en accord avec l'expérience. ... .... QUESTION 1 Pour chacune des deux questions suivantes, une seule des quatre réponses est exacte. Aucune justification n’est demandée. Une bonne réponse rapporte un demi-point. Une mauvaise réponse, plusieurs réponses ou l’absence de réponse ne rapportent, ni n’enlèvent aucun point. Indiquer sur la copie le numéro de la question et la réponse choisie.  1. Le nombre ln(35) est égal à :  a. ln(5)×ln(7) ;  b. ln(5)+ln(7) vrai ; c. ln(30)+ln(5) ; d. ln(30)×ln(5). ln(35) = ln(5 x7) = ln(5) + ln(7).  2. Le nombre e20 est égal à : a. e 4 ×e 5 ; b. e 4 + e 5 ; c. e 5 +e 15 ; d. e 5 ×e 15 vrai. e20 = e5 +15 =e 5 ×e 15 . QUESTION 2 Lors d’une course, on a mesuré la fréquence cardiaque d’un coureur de 100 m. Cette fréquence cardiaque, en battements par minute, est modélisée par la fonction f définie sur [0; 100] par f (x) = 28 ln(x +1)+70 où x est la distance parcourue, en mètre, depuis le départ de la course.  1. Selon ce modèle, quelle est la fréquence cardiaque de ce coureur au départ de la course ? x = 0 ; f(0) =ln(1) +70 = 0 +70 = 70 battements / minute. 2. Selon ce modèle, au bout de combien de mètres la fréquence cardiaque de ce sportif est-elle égale à 185 battements par minute ? Arrondir à l’unité. 28 ln(x +1)+70 = 175 ; 28 ln(x+1) = 105 ; ln(x+1) = 105 / 28 = 3,75. x+1 = e3,75 ~ 42,52  ; x ~ 42  m. QUESTION 3 La température d’un four, exprimée en degré Celsius, en fonction du temps t, exprimé en minute, est modélisée par une fonction f définie et dérivable sur [0; +∞[, solution de l’équation différentielle (E) : y ′ = −0,2y +44.  1. Déterminer les solutions de cette équation différentielle sur [0; +∞[. Solution générale de y' +0,2 y = 0 : y = A e-0,2t avec A une constante. Solution particulière de (E) : y = 44 / 0,2 =220. Solution générale de (E) : y = A e-0,2t + 220.  2. On suppose que la température initiale du four est 25°C. En prenant f (0) = 25, donner une expression de f (t), pour tout t de [0; +∞[. 25 = A +220 ; A = -195. f(t) =220 -195 e-0,2t. QUESTION 4 On note i le nombre complexe de module 1 et d’argument p/ 2 : On pose z =3½−i et z ′ = −2½exp(ip/4). 1. Déterminer la forme exponentielle de z. Détailler les calculs. |z| = (3+(-1)2)½ =2. z / |z| = 3½ /2 -0,5 i =cos (-p/6) + i sin (-p / 6). z = 2 exp(-ip /6). 2. En déduire la forme exponentielle de z / z ′ . z ′ = −2½exp(ip/4) = z ′ = 2½exp(ip/4) x exp(ip) = 2 exp(i 5p/4). z / z' = 2½ / 2 exp(ip/4) x exp( -i 5p/4) = 1 /2½ exp( -ip) = -1 /2½ .  QUESTION 5 L’iode 131 est un élément radioactif qui se désintègre selon la loi N(t) = N(0)e−O,086t , où N(0) est le nombre de noyaux au début de l’observation et N(t) le nombre de noyaux à l’instant t, exprimé en jour. Déterminer le temps au bout duquel la moitié des noyaux d’iode 131 se sont désintégrés (demi-vie). On donnera le résultat en nombre de jours arrondi à l’unité. N(t½) = N(0) / 2 = N(0) exp(-0,086 t½). 0,5 = exp(-0,086 t½). ln(0,5) = -0,086 t½ ; t½ ~ 8,0 jours.  QUESTION 6 On considère la fonction f définie sur R par f (x) = sin(x)+cos(x), 1. Montrer que f est solution de l’équation différentielle y ′′ + y = 0. f '(x) = cos(x) - sin(x). f "(x) = -sin(x) -cos(x). f "(x) + f(x) = 0.  2. Montrer que, pour tout nombre réel x, f (x) = 2½cos ( x − p / 4 ).  f '(x) = - 2½ sin ( x − p / 4 ). f "(x) = - 2½ cos ( x − p / 4 ). - 2½ cos ( x − p / 4 ) +2½cos ( x − p / 4 )=0 est vérifié quel que soit x.

menu