Le lob parfait au squash, panneaux photovoltaïques, Bac STL 09 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le lob parfait au squash. Le squash est un sport de raquette qui se joue sur un terrain de jeu entièrement entouré de murs ou éventuellement de parois vitrées. Les deux joueurs sont sur la même partie du terrain et jouent à tour de rôle. Chaque joueur frappe à l’aide d’une raquette une petite balle noire en caoutchouc, de telle sorte que son adversaire ne puisse pas la reprendre. L’un des coups possibles est le lob : il s’agit souvent d’un coup défensif qui consiste à frapper la balle de bas en haut sur le mur frontal dans le souci de la faire passer au-dessus de l’adversaire et de l’amener dans le fond du terrain. Le lob parfait impose que la balle atteigne une hauteur h en sommet de trajectoire comprise entre 4,0 m et 4,5 m : assez haute pour passer au-dessus du joueur et pas trop haute afin qu’elle ne sorte pas du terrain. 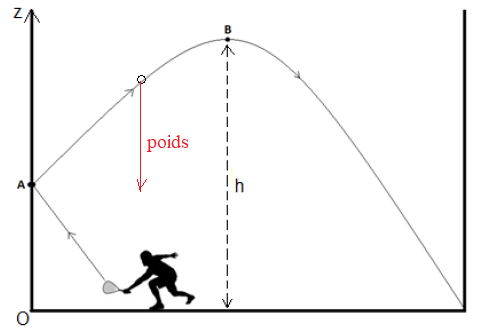Le mouvement de la balle est étudié dans un référentiel terrestre supposé galiléen, d’un point A à un point B : le point A désigne l’impact de la balle sur le mur frontal, le point B est le sommet de la trajectoire de la balle lors du lob. L’axe vertical (Oz) du repère choisi dans le référentiel terrestre est orienté vers le haut, son origine O est l’angle du mur frontal. Dans cette étude, on supposera que les forces de frottements s’exerçant sur la balle sont négligeables. Données relatives à la balle : - Altitude au point A : zA = 3,2 m - Altitude au point B : zB = h - Vitesse au point A : vA = 24 km.h-1 - Vitesse au point B : vB = 17 km.h-1 - Masse de la balle : m = 25 g Intensité de la pesanteur terrestre : g = 9,8 m.s-2. L’objectif de l’exercice est de déterminer si le lob correspondant aux données précédentes peut être considéré comme parfait. 1. Nommer la force exercée sur la balle pendant son mouvement entre A et B, puis donner son expression littérale. Calculer sa valeur et la représenter sur le document. Le poids de la balle P = mg = 0,025 x9,8 =0,245 ~0,25 N. 2. Donner l’expression littérale du travail de cette force appliquée à la balle lors de son déplacement de A vers B. 3. En déduire, sans le calculer, si ce travail est moteur, résistant ou nul. Expliquer en quoi cela est cohérent. Travail résistant, négatif, en montée : W = mg ( zA-zB). 4. Exprimer l’énergie potentielle de pesanteur Ep de la balle, puis calculer sa valeur au point A que l’on notera Ep(A). Ep(A) = mg zA =0,025 x9,8 x3,2 =0;784 ~0,78 J. 5. Exprimer l’énergie cinétique Ec de de la balle au point A, notée Ec(A). Calculer sa valeur après avoir réalisé les conversions d’unités nécessaires. Ec(A) = 0,5 m v2A avec vA = 24 / 3,6 ~6,67 m /s. Ec(A) = 0,5 x 0,025 x 6,672 ~0,56 J. 6. Donner l’expression de l’énergie mécanique Em(A) de la balle au point A. Vérifier qu’elle est environ égale à 1,3 J. Em(A) = Ep(A) + Ec(A) = 0,78 +0,56 ~1,3 J. 7. Donner l’expression littérale de l’énergie mécanique Em(B) de la balle au point B en fonction des grandeurs m, g, zB et vB. Em(B) = mgzB + ½mv2B. 8. En appliquant le principe de conservation de l’énergie mécanique Em, déterminer si, sur cet essai, le lob peut être considéré comme parfait. Em(A)=Em(B) ; mgzB + ½mv2B = 1,3 mgzB = 1,3 -½mv2B ; zB =1,3 / (mg) -0,5 v2B / g ; vB = 17 / 3,6 ~4,7 m /s. zB = 1,3 /(0,025 x9,8) -0,5 x4,72 / 9,8 ~4,2 m. Le lob est donc parfait. ... .... Panneaux photovoltaïques. Pour la production d’énergie électrique d’un site isolé, occupé quelques mois par an, les propriétaires envisagent l’installation de panneaux photovoltaïques. Ils estiment la puissance électrique nécessaire à leur mode de vie à 6 kW. La moitié de la toiture a une exposition plein sud, adaptée à la pose de panneaux photovoltaïques. Sa surface est estimée à environ 50 m². L’inclinaison recommandée par les installateurs est adaptée pour une utilisation estivale, un peu moins pour l’hiver. L’objectif de cet exercice est d’étudier l’opportunité de l’installation. 1. Compléter le schéma de la chaîne énergétique en faisant apparaître les différentes formes d’énergie. Les panneaux photovoltaïques sont constitués de cellules au silicium cristallin fonctionnant sur un domaine de longueurs d’onde compris entre 0,4 et 1,1 μm. 2. En utilisant le profil spectral solaire reçu au niveau du sol présenté sur la figure suivante, expliquer pourquoi les cellules au silicium sont adaptées pour être utilisées sur un panneau photovoltaïque. L'irradiance solaire présente un maximum entre 0,4 et 1,1 µm. 3. Surface d’un panneau S = 1,61 m2, puissance nominale maximale 265 W ; rendement 16,5 %. Calculer la puissance lumineuse reçue par un seul panneau photovoltaïque, sous une condition d’éclairement moyen de 1000 W.m-2. 265 / 0,165 = 1,6 103 W. Les caractéristiques intensité-tension d’un panneau photovoltaïque sont données. Chacune de ces caractéristiques est tracée pour un éclairement moyen différent : de 400 W.m-2 correspondant à un ciel partiellement nuageux à 1000 W.m-2 correspondant à un ciel totalement dégagé. Cela permet de déterminer la réponse d’un panneau en fonction du contexte d’exposition solaire. 4. Proposer une estimation de la valeur de la puissance électrique maximale que peut délivrer un panneau pour un ciel totalement dégagé. Puissance nominale  = 9 x 30 = 270 W. 5. Commenter le résultat obtenu à la question 4 compte tenu du tableau de données constructeur précédent. En accord avec 265 W. 6. Définir le rendement d’un panneau photovoltaïque. Montrer que sa valeur16,5 %, est cohérente avec la valeur de la puissance nominale maximale et celle de la puissance lumineuse calculée à la question 3. Rendement = puissance électrique nominale / puissance solaire. 270 / (1,6 103) ~0,17. 7. Calculer le nombre de panneaux nécessaires pour assurer les besoins énergétiques des propriétaires du chalet pour un ciel totalement dégagé. En déduire la surface de toiture qu’occuperait l’ensemble de ces panneaux. 6 / 0,265 =22,6 soit 23 panneaux. Surface des panneaux = 23 x1,61 ~37 m2. 8. Reprendre la question précédente dans le cas d’un ciel partiellement nuageux (éclairement moyen de 400 W.m-2). Puissance nominale 4,7 x32 ~150 W. Nombre de panneaux : 6 / 0,15 ~40. Surface des panneaux : 40 x1,61 ~64 m2. 9. Discuter la faisabilité du projet des propriétaires à la lumière des résultats précédents. Cette dernière valeur étant supérieure à la surface du toit, le projet n'est pas réalisable, sauf si on stocke l'excès d'énergie lors d'un ciel totalement dégagé.

menu