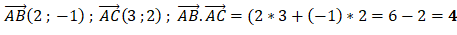Question 1
Soit la fonction 𝑓 définie sur [0; +∞[ par f(x) =
(−4𝑥 + 8)𝑒
−𝑥 .
Montrer que 𝑓(0) est un nombre entier que l'on précisera.
f(0) = (-4*0 +8 e
0 =8*1=
8.
Question 2
Déterminer la limite en plus l'infini de f(x).
En plus l'infini :
e
-x tend vers zéro ;
-4x+8 tend vers moins l'infini ;
par produit des limites, f(x) tend vers zéro.
Question 3.
Soit la fonction f définie et dérivable sur [0; +∞[ par f(x) = (−4𝑥 +
8)𝑒
−𝑥.
On note f ' sa fonction dérivée.
Déterminer f '(𝑥) pour tout 𝑥 appartenant à l’intervalle [0 ; + ∞[.
On pose u = -4x+8 et v = e
-x.
u' = -4 ; v' = -e
-x.
u'v +v'u = -4e
-x-(-4x+8)e
-x=(4x-12)e
-x.
Question 4.
Écrire 𝐴 sous la forme e
n, n étant un nombre entier relatif.
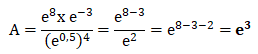Question 5
Sachant que cos (9
p
/5 )= (5
½+1) / 4, exprimer cos (
p/5) en fonction de 5
½.
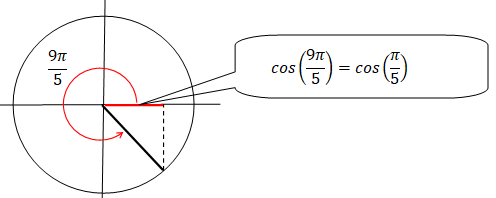
cos(10
p/5-
p/5)=cos(2
p-
p/5)=cos(
-p/5)=cos(p/5).
Question 6.
Déterminer le produit scalaire suivant :
