Mathématiques,
physique chimie, bac STL Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 4 points
On souhaite déterminer le temps de demi-réaction de la saponification
de l’éthanoate d’éthyle par deux méthodes : un suivi cinétique pH-métrique (partie A)
puis l’exploitation mathématique de la loi de vitesse (partie B). L’équation de la réaction
modélisant cette transformation chimique est :

Données :
- masse volumique de l’éthanoate d’éthyle : ré.é.= 0,925 g/mL ;
- masse molaire de l’éthanoate d’éthyle : Mé.é.= 88,0 g/mol ;
Partie A : suivi pH-métrique de la saponification (physique-chimie, 2 points)
Le suivi est réalisé en mettant en oeuvre le protocole suivant :
- dans un bécher, verser :
10,0 mL de soude à 0,10 mol/L ;
environ 35 mL d’eau ;
environ 15 mL d’éthanol ;
2,0 mL d’éthanoate d’éthyle.
- déclencher l’acquisition informatique de la mesure du pH toutes les
secondes. Le déclenchement définit l’instant initial t = 0 s.
1. Déterminer les valeurs des quantités de matière initiales d’éthanoate d’éthyle et de soude.
n(éthanoate) =2,0 ré.é./ Mé é =2,0 x0,925 /88,0=0,021 mol.
Dans
ces conditions, on considère que la concentration en éthanoate d’éthyle
reste constante et égale à sa valeur initiale tout au long de la
transformation chimique. La loi de vitesse de réaction peut alors
s’écrire comme celle d’une loi d’ordre 1 :
v = k1 [HO‒] dans laquelle k1 est appelée constante de vitesse apparente.
On souhaite établir la relation entre le pH mesuré et la concentration
en quantité de matière C en ions hydroxyde dans le mélange réactionnel
au même instant.
2. Écrire l’équation de la réaction d’autoprotolyse de l’eau.
2H2O (l) = H3O+aq + HO-aq.
3. Donner
l’expression de la constante d’équilibre Ke de la réaction
d’autoprotolyse de l’eau en fonction des concentrations à l’équilibre.
Ke = [H3O+aq] [HO-aq].
4. En déduire la relation entre la concentration C en ions hydroxyde et le pH mesuré à tout instant.
C =[HO-aq] =Ke /[H3O+aq] = Ke / 10-pH = Ke x 10pH.
A
partir des valeurs du pH mesuré à chaque seconde et en utilisant la
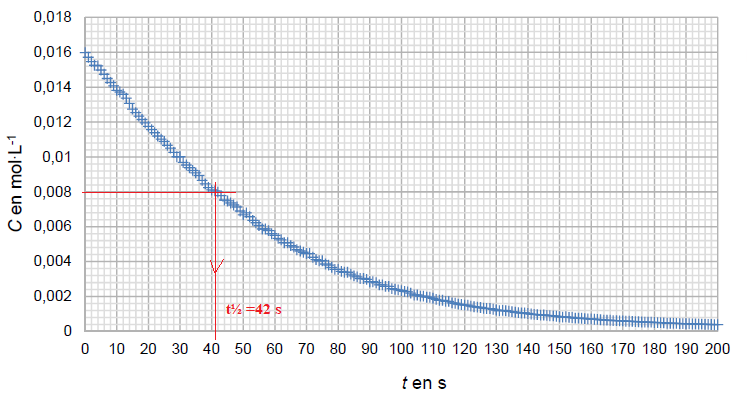
relation entre C et le pH, on obtient le graphique suivant.
5. Déterminer le temps de demi-réaction t½, exprimé en seconde, de la saponification. Une justification graphique est
attendue.
Partie B : (mathématiques, 2 points)
On note C(t) la concentration en ions hydroxyde, exprimée en mol/L, à l’instant t, exprimé en seconde et C0 la concentration en ions hydroxyde à l’instant t = 0.
Dans les conditions décrites dans la partie A, C0 = 0,016 mol/L et k1= 0,017 s-1.
La fonction C est donc solution de l’équation différentielle (E) suivante :
y' = − k1y (E)
1. Vérifier que la fonction C définie sur [0 ; +∞[ par C(t) = C0e-k1t est une solution de (E).
C'(t) = -k1 C0e-k1t ; repport dans (E) :
-k1 C0e-k1t =-k1 C0e-k1t est vérifiée quel que soit t.
Montrer que C(0) = C0. On admet que C est la seule solution de (E) qui vérifie C(0) = C0.
C(0) = C0e-0 = C0.
2. Déterminer
par le calcul le temps de demi-réaction t½. On donnera la valeur
exacte, puis l’arrondi à la seconde. Interpréter ce résultat dans le
contexte de l’exercice.
C(t½) = 0,5 C0 = C0e-k1t½ ; 0,5 = e-k1t½ ;0,5 = e-0,017t½ ;
ln(0,5) = -0,017 t½ ; t½ = - ln(0,5) / 0,017 = ln(2) / 0,017 ~41 s.
A t = 41 s, la concentration en ion hydroxyde est divisée par 2.
Exercice 2. 6
points.
Pour alimenter un appareil auditif, deux types de piles boutons sont disponibles :
- une pile bouton zinc-manganèse ;
- une pile bouton zinc-air.
L’objectif de l’exercice est de déterminer la pile à privilégier pour
une plus grande autonomie de fonctionnement de l’appareil auditif.
Données :
- masses molaires atomiques : M(Zn) = 65 g∙mol-1 ; M(Mn) = 55 g∙mol-1 ;
Partie A : étude de la pile zinc-manganèse
Dans une pile bouton zinc-manganèse, une électrode contient du zinc Zn(s) et l’autre du dioxyde de manganèse MnO2(s)
et du carbone C(s). Le carbone n’intervient pas dans le couple de la
demi-pile mais permet notamment la conduction du courant.
Afin de déterminer la polarité de la pile, on branche la borne COM d’un
voltmètre à l’électrode de carbone et la borne V à l’électrode de zinc,
on mesure alors une tension de −1,50 V.
1. Déduire de cette mesure de la tension à vide la polarité de chaque électrode en précisant le raisonnement.
Le
volmètre indique une valeur négative ; il est branché à l'envers, le
carbone est la borne positive et le zinc la borne négative.
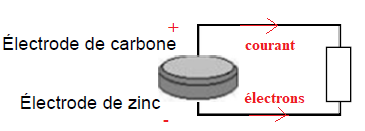
2. Indiquer la polarité des bornes de la pile, le sens de déplacement des électrons ainsi que le sens du courant.
Les demi-équations électrochimiques se produisant aux électrodes de la pile sont les suivantes :
Zn(s) + 2 HO‒(aq) → ZnO(s) + H2O(ℓ) + 2 e‒
MnO2(s) + H2O(ℓ) + 1 e‒ → MnO2H(s) + HO‒(aq)
3. Associer chaque
demi-équation électrochimique à l’électrode correspondante et préciser
si elle est le siège d’une oxydation ou d’une réduction.
Oxydation du zinc à l'anode négative : Zn(s) + 2 HO‒(aq) → ZnO(s) + H2O(ℓ) + 2 e-.
Réduction de MnO2 (s) à la cathode positive : MnO2(s) + H2O(ℓ) + 1 e‒ → MnO2H(s) + HO‒(aq)
4. Établir l’équation de la réaction modélisant le fonctionnement de la pile, en précisant la démarche.
Zn(s) + 2 HO‒(aq) → ZnO(s) + H2O(ℓ) + 2 e-.
2 fois { MnO2(s) + H2O(ℓ) + 1 e‒ → MnO2H(s) + HO‒(aq) }.
Ajouter : Zn(s) + 2 HO‒(aq) +2MnO2(s) + 2H2O(ℓ) + 2 e‒ → ZnO(s) + H2O(ℓ) + 2 e- +2MnO2H(s) + 2HO‒(aq).
Simplifier : Zn(s) + 2MnO2(s) + H2O(ℓ) → ZnO(s) +2MnO2H(s) .
5. Sachant que la masse initiale de l’électrode en zinc est mZn= 55 mg, déterminer la quantité de matière initiale de zinc nZn présente dans la pile.
nZn = mZn/ V = 0,055 / 65 ~8,5 10-4 mol.
6. En admettant que le zinc est entièrement consommé et que le dioxyde de manganèse MnO2(s) est en excès, déduire la quantité de matière ne- d’électrons échangés au cours de la transformation chimique.
ne- = 2 nZn = 1,7 10-3 mol.
7. Vérifier que la valeur de la quantité d’électricité disponible dans la pile est voisine de Q1 = 164 C.
Q1 = ne- F = 1,7 10-3 x96500 ~163 C.
8. Calculer la durée de fonctionnement de la pile zinc-manganèse. I = 2,0 mA)
t = Q1 / I = 164 / (2,0 10-3) =8,2 104 s ( 22 h 42 min).
Partie B : étude de la pile zinc-air.
L’équation de la réaction modélisant le fonctionnement de la pile
correspond à l'oxydation du zinc en oxyde de zinc par le dioxygène de
l'air :
2 Zn(s) + O2(g) → 2 ZnO(s)
Un des deux couples redox mis en jeu est le couple O2(g)/H2O(ℓ).
1. Écrire l’équation de demi-réaction électrochimique correspondant à ce couple et justifier le caractère oxydant du dioxygène.
Le dioxygène gagne des électrons, c'est un oxydant qui se réduit :O2(g) + 4e- +4H+aq --> 2H2O(ℓ)
2. Calculer la durée de fonctionnement de la pile zinc-air en vous aidant de ses caractéristiques.
Q = 182 mA h ; I = 2,0 mA.
Durée de fonctionnement : 182 / 2 = 91 heures.
Partie C : choix de la pile à privilégier
À l’aide des parties A et B et des informations disponibles, indiquer
le type de pile qu’il faudrait privilégier pour l’alimentation d’un
appareil auditif. Justifier la réponse.
La pile zinc-air est à privilégier, elle assure une plus grande autonomie.
|
...
|
....
|
Exercice 3 (4 points)
Q 1.
On donne ci-dessous un tracé de la courbe représentative C d’une fonction f définie sur R.
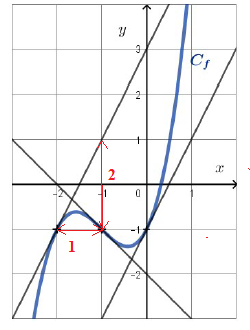
f '(-2) est égale à a. 0 ; b. 2 vrai ; c. -1 ; d. -2,25.
Le coefficient directeur de cette tangente vaut 2.
Q2 On considère l’équation ln(x) = 7. Cette équation admet pour solution :
a. ln(7) ; b. ln(e7) ; c. e7 vrai ; d. 1/7.
Q3 - On considère la fonction f définie sur R par f(x) = x e2x .
Déterminer f '(x), où f ' est la fonction dérivée de la fonction f. Justifier la réponse.
On pose u = x et v = e2x ; u' = 1 ; v' = 2 e2x.
u'v+v'u=e2x+2x e2x=e2x(2x+1).
Q4 -Soit ABCD un carré de côté 4 cm. Calculer le produit scalaire suivant.
Justifier la réponse.
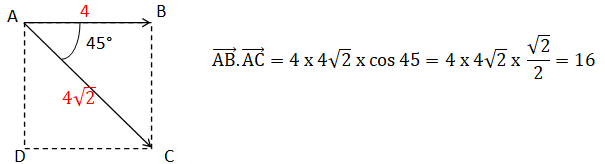
Q5 - On considère l’équation différentielle suivante :
v′ = −4,5v + 6,3 (E)
Déterminer la fonction v solution de l’équation (E) et vérifiant la condition initiale v(0) = 0.
Solution générale de v'+4,5 v=0 : v = A e-4,5x avec A une constante.
Solution particulière de (E) : v = 6,3 / 4,5 =1,4
Solution générale de (E) : v = A e-4,5x +1,4.
v(0) = A+1,4 =0. A = -1,4.
v = -1,4 e-4,5x +1,4.
Q6 Afin
d’étudier l’évolution d’une population de bactéries à l’intérieur d’une
boîte fermée, on considère la fonction 𝑓 définie pour tout 𝑡 ≥ 0 par
f(t) =100 / (1+e-1,3t) où f(t) désigne le nombre de bactéries (exprimé en millier) à l’instant t (exprimé en heure).
Le
programme en Python suivant affiche la valeur de t (arrondie à l’unité)
à partir de laquelle le nombre de bactéries à l’intérieur
de l’enceinte dépasse 99 000.
Quelle est la valeur affichée lorsqu’on exécute ce programme ?
from math import exp
T=0
while 100 / (1+exp(-1,3xT) <=99
T=T+1
print(T)
100 / (1+e-1,3t) > 99 ; 100 > 99(1+e-1,3t) ; 1>99e-1,3t ;1 / 99 >e-1,3t ;
ln(1 / 99) >-1,3 t ; -ln(99) >-1,3 t ; ln(99) < 1,3 t ; t > ln(99) / 1,3 ; t >3,53.
Le programe affiche 4.
Exercice 4 – A – PANNEAU PHOTOVOLTAÏQUE
Mots clés : physique ; puissance ; générateur d’énergie électrique
L’exercice vise à vérifier si un panneau photovoltaïque fonctionne toujours correctement.
Le graphique qui représente l’intensité I, en mA, en fonction de la
tension aux bornes du panneau photovoltaïque U, en V, est appelé
caractéristique courant-tension. Ce graphiquenous renseigne sur le
comportement du panneau photovoltaïque.
1. Proposer un
schéma du dispositif expérimental permettant de mesurer la tension aux
bornes du panneau photovoltaïque et l'intensité du courant qui le
traverse lorsque l'on fait varier la valeur de la résistance R placée
aux bornes du panneau.
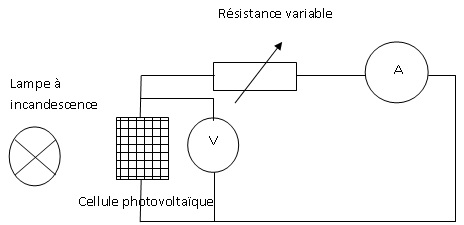
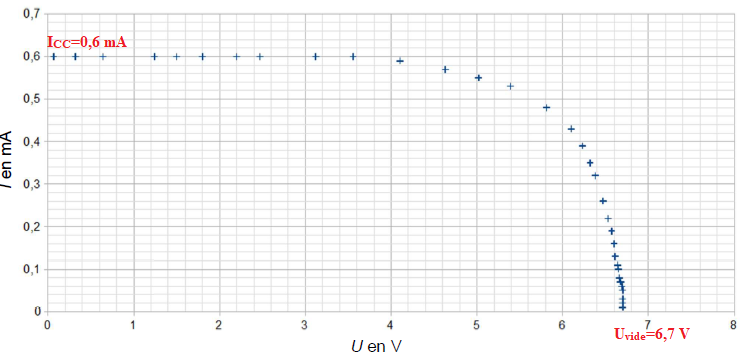
Pour un éclairement énergétique de 96,6 W/m², on obtient la caractéristique suivante :
2. Déterminer, en précisant la démarche utilisée, la valeur de la tension à vide Uvide de la cellule photovoltaïque.
3. Déterminer, en précisant la démarche utilisée, la valeur de l’intensité de court-circuit Icc.
Les caractéristiques obtenues avec deux autres valeurs d’éclairement énergétique sont tracées sur le même graphique ci-après.
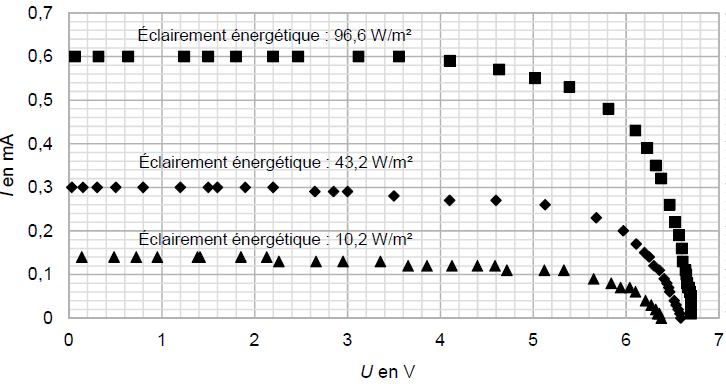
4. À partir des caractéristiques obtenues, décrire soigneusement l’influence de l’éclairement énergétique sur la tension à vide Uvide et sur l’intensité de court-circuit Icc.
Si l'éclairement diminue :
Uvide décroit légèrement , tandis que ICC décroît fortement et se rapproche de zéro.
Dans toute la suite, l’éclairement énergétique est fixé à 96,6 W/m².
L’étape suivante consiste à déterminer la puissance maximale de
fonctionnement du panneau.
5. Donner la relation permettant de calculer la puissance électrique Pélec fournie par un dipôle en précisant les grandeurs physiques et leur unité.
Pélec = U x I avec Pélec ( watt); U (volt) ; I (ampère).
Les courbes représentatives de l’intensité I et de la puissance Pélec en fonction de la tension U aux bornes du panneau photovoltaïque sont représentées sur le même graphique.
6. Déterminer graphiquement les valeurs de la puissance électrique maximale Pmax, de la tension UPmax et de l’intensité IPmax du
panneau photovoltaïque lorsque la puissance électrique délivrée par ce
dernier est maximale. Vérifier la cohérence de ces trois valeurs.
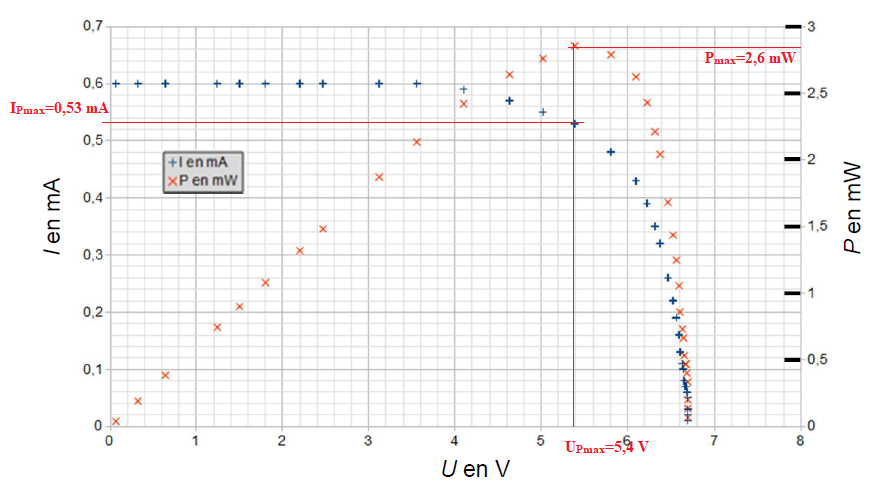
UPmax x IPmax = 5,4 x0,53 ~2,8 mW peu différent de Pmax.
On souhaite maintenant déterminer la valeur du rendement du panneau
photovoltaïque lorsque la puissance électrique est maximale, pour un
éclairement énergétique de 96,6 W/m².
7. Donner l’expression du rendement du panneau photovoltaïque en fonction de la puissance électrique Pélec et de la puissance lumineuse Plum reçue.
Rendement = Péle / Plum.
8. Le panneau
photovoltaïque a la forme d’un rectangle de dimensions 4,8 cm x 6,4 cm.
Il est éclairé sous 96,6 W/m². Calculer le rendement du panneau
lorsqu’il délivre sa puissance électrique maximale et l'exprimer en
pourcentage. Commenter la valeur obtenue et conclure sur le
fonctionnement de ce panneau photovoltaïque.
Surface du panneau : 4,8 x6,4 =30,72 cm2 = 3,072 10-3 m2.
Plum = 96,6 x 3,072 10-3 ~0,30 W = 300 mW.
Rendement = 2,6 / 300 ~0,009 ( 0,9 %).
Le rendement est très faible sous ce faible éclairement ( 10 % du rayonnement solaire habituel).
EXERCICE 4 – B – CHUTE DE GRÊLONS
Mots-clés : bilan des forces ; énergie mécanique ; travail des forces de frottement.
Régulièrement, de fortes intempéries sont l’occasion de constater les importants dégâts causés par les chutes de grêlons.
Ainsi, un grêlon de masse m = 13,0 g qui chute d’une altitude initiale
h = 1 600 m sans vitesse initiale peut atteindre au sol une vitesse vsol = 100 km.h-1.
Dans cette étude, on assimile le système grêlon à un point matériel ; son centre de masse est noté G.
1. Donner la forme d’énergie responsable des dégâts occasionnés par un orage de grêle.
Energie cinétique.
2. Après avoir
précisé le référentiel d’étude, effectuer un bilan des forces
extérieures appliquées au système {grêlon}. Donner leurs
caractéristiques (direction, sens et norme), puis les représenter sans
considération d’échelle.
Poids, verticale vers le bas, valeur mg et forces de frottement dues à l'air, verticale, vers le haut.
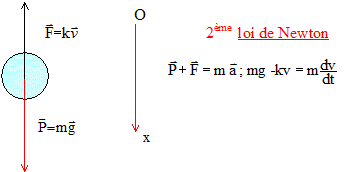
3. Modèle de la chute libre
Donnée : la chute libre est un modèle qui suppose que la seule force
exercée sur le système étudié est le poids. Les lois de Newton
permettent alors d’établir que, dans ce cas, le vecteur
accélération est :
- de direction verticale ;
- orienté vers le bas ;
- de valeur égale au champ de pesanteur terrestre g = 9,81 m.s-2.
3.1. Justifier la conservation de l’énergie mécanique lors de la chute du grêlon.
La seule force qui travaille est le poids, cette force étant conservative, l'énergie mécanique reste constante.
3.2. Calculer la valeur de l’énergie mécanique du grêlon à la position initiale au point A d'altitude h = 1600 m.
L’énergie potentielle de pesanteur est égale à 0 au niveau du sol.
l'énergie mécanique est sous forme potentielle mgh = 0,013 x1600 x9,81 ~204 J.
3.3. Déterminer la valeur, en km.h-1,
de la vitesse du grêlon, notée v, lorsqu’il arrive au sol après le
mouvement en chute libre. On utilisera la conservation de l’énergie
mécanique.
Au sol l'énergie mécanique est sous forme cinétique ½mv2.
v2 = 2 x204 / 0,013 =31 392 ; v =177 m /s ou 177 x3,6 ~638 km /h.
3.4. En comparant
la vitesse du grêlon obtenue à la question précédente et celle mesurée,
discuter la validité, dans le cas étudié, du modèle de la chute libre.
Le modèle de la chute libre n'est pas valide.
4. Prise en compte de l’action de l’air sur la chute du grêlon
4.1. Déterminer la variation de l’énergie mécanique du système en tenant compte de l’action de l’air sur le grêlon.
Energie cinétique en arrivant au sol : 0,5 x0,013 x(100 / 3,6)2 ~5,0 J.
Variation de l'énergie mécanique =5-204= -199 J.
4.2. Déduire la valeur du travail de la force de frottement qui modélise l’action de l’air sur le grêlon. Commenter.
La diminution de l'énergie mécanique est due au travail des frottements.
Travail des frottements : -199 J.
Les frottements sur les couches d'air diminue fortement la vitesse de chute.
|
|