Une
solution innovante consiste à remplacer les batteries
des bus électriques par des supercondensateurs.
Le principe est le suivant : à chaque arrêt, le bus se connecte de manière automatique et rapide
au totem. Le transfert d’énergie électrique entre les supercondensateurs du totem et les
supercondensateurs embarqués dans le bus s’effectue alors en environ 10 s. Cette phase,
appelée « biberonnage », doit être parfaitement sécurisée. En effet, l’intensité du courant
électrique peut atteindre plusieurs milliers d’ampères en début de transfert.
A. Étude d’un supercondensateur.
Chaque supercondensateur utilisé dans le totem a une tension nominale E. Il s’agit de la tension
atteinte lorsque le supercondensateur de capacité C est totalement chargé.
Après avoir chargé complètement un supercondensateur sous sa tension nominale E, on le place
dans le circuit schématisé sur la figure ci-dessous. Et à l’instant t = 0, on bascule l’interrupteur K
en position fermée.
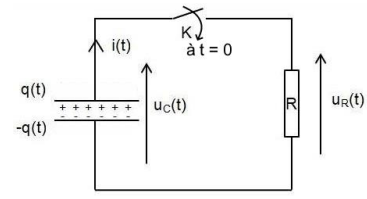
On désigne par q(t) la charge électrique portée par l’armature positive du condensateur à
l’instant t comme indiqué sur le schéma du circuit.
Données :
- valeur initiale de la tension aux bornes du condensateur : u
C(0) = E = 2,7 V ;
- valeur de la résistance : R = 100 ± 2 m
W où ce qui suit le ± est l’incertitude-type.
A.1. Montrer qu’au cours de la décharge l’intensité i(t) s’exprime par :
i(t) = - C x
du
c
(t)
dt.
q =Cu
c ; i = -dq /dt =
-C x
duc
(t)
dt.
A.2. En déduire que la tension u
C(t) obéit à l’équation différentielle :
RC x
du
c
(t)
dt
+u
c
(t) = 0.
u
c(t) = u
R(t) = R i(t) = - RC
duc
(t)
dt.
RC
duc
(t)
dt + uc(t) = 0.
La solution de cette équation différentielle est de la forme : u
c
(t) = A + B x exp(
-
t
/ (RC)).
A.3. En détaillant la démarche, déterminer les valeurs de A et B.
uc(0) = E = A+B.
A t très grand, le terme en exponentielle est nul . Le supercondensateur s'est déchargé dans R et u
c = 0.
Donc A = 0 ; par suite B = E.
uc
(t) = E x exp(
-
t
/ (RC)).
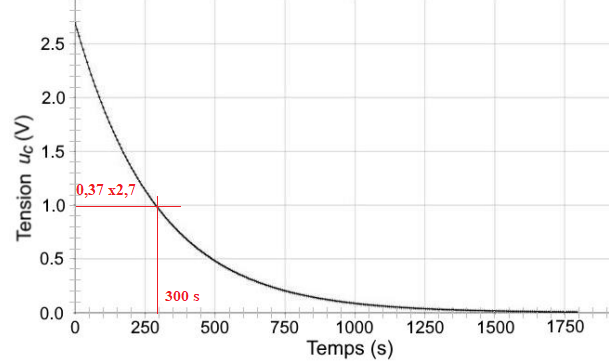
Un dispositif d’acquisition permet d’enregistrer l’évolution de la tension u
C(t) lors de la décharge
du supercondensateur. On obtient alors la courbe suivante.
A.4. Déterminer le temps caractéristique
t de la décharge. Faire apparaître la construction
graphique réalisée sur la courbe.
 5.
5. En déduire la valeur de la capacité du supercondensateur utilisé dans cette étude.
Commenter l’ordre de grandeur obtenu.
RC = 300 ; R =0,100 ohm ; C = 300 / 0,100 = 3,0 10
3 F, valeur très grande par rapport aux capacités usuelles.
L’incertitude-type sur la lecture graphique de
t est estimée à u(c) = 25 s.
L’incertitude-type u(c) sur la capacité C peut se calculer à partir de la relation :
u(c) = C × [(u(
t) /
t)
2 +(u(
R) / R)
2]
½
où u(x) désigne l’incertitude-type sur la grandeur x.
A.6. Calculer u(
C) et exprimer le résultat de la mesure avec son incertitude-type. Comparer la
valeur expérimentale à la valeur de référence annoncée par le constructeur C
réf = 3000 F.
u(c) = 3000 × [(25 / 300)2 +(2 / 100)2]½ =3000 x 0,087 =260 F
C = 3000 ±260 F.
Ces deux valeurs sont en accord.
B. Étude du totem
Le totem contient une association d’un grand nombre de supercondensateurs. Cette association
se comporte comme un unique condensateur, appelé condensateur totem, de capacité notée
C
totem = 20 F. La tension nominale du condensateur totem a pour valeur E
totem = 760 V.
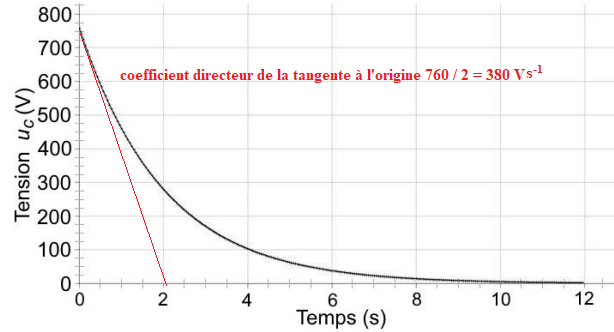
La courbe ci-après représente l’évolution temporelle de la tension u
C lors de la décharge du
condensateur totem dans une résistance.
B.1. Déterminer la valeur de l’intensité maximale I
max lors de la phase de décharge.
Commenter.
I
max = C
totem dUc / dt = 20 x 380 =7,6 10
3 A.
L’énergie W emmagasinée dans le condensateur totem est donnée par la relation :
W = 0,5
× C
totem × u
c
2
avec l’énergie W en joule, la capacité C
totem en farad et la tension du condensateur u
c en volt.
Pour recharger le condensateur totem, on utilise le réseau électrique fournissant une puissance
supposée constante de valeur 9,0 kW.
B.2. Estimer le délai minimal à respecter entre le passage de deux bus au totem.
W = 0,5 x20 x 760
2 =5,78 10
6 J.
Délai minimal = W / P =
5,78 106 / (9,0 103)=6,4 102 s ( 10 min 42 s).