Mathématiques, brevet DNB, Asie Pacifique 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 20 points. Situation 1. On considère le programme de calcul ci-dessous : Nombre de départ. Soustraire 7. Multiplier par 5. Soustraire le double du nombre de départ. Résultat.  1) Montrer que si le nombre de départ est 10, le résultat obtenu est −5. 10-7=3. 3 * 5 = 15. 15 -20 = -5.  2) On note x le nombre de départ auquel on applique ce programme de calcul. Parmi les expressions suivantes, quelle est celle qui correspond au résultat du programme de calcul ? Aucune justification n’est attendue pour cette question. Expression A : 𝑥 − 7 × 5 − 2𝑥  Expression B : 5(𝑥 − 7) − 2𝑥  Vrai. Expression C : 5(𝑥 − 7) − 𝑥 2 Expression D : 5𝑥 − 7 − 2x. Situation 2 :  Dans le repère ci-dessous, la droite (d) représente une fonction linéaire f. Le point A appartient à la droite (d). 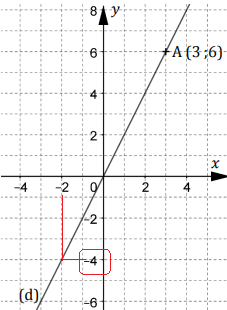1) À l’aide du graphique, déterminer l’image de − 2 par la fonction f. 2) Déterminer une expression de f(x) en fonction de x. La doite passe par l'origine et son coefficient directeur est 6 / 3 = 2. Donc f(x) = 2x. Situation 3 : Le dessin ci-dessous représente une pyramide de sommet G et dont la base CDEF est un rectangle. Le volume de cette pyramide est-il supérieur à 20 L ? 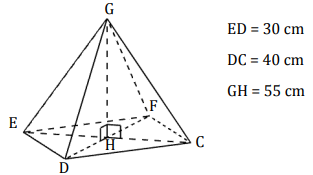Aire de la base : 3 x 4=12 dm2. Volume = aire de base x hauteur / 3 = 12 x 5,5 /3 =4 x5,5 = 22 dm3=22 L supérieur à 20 litres. ..   Exercice 2 ( 20 points) La figure ci-desous est réalisée à main levée. 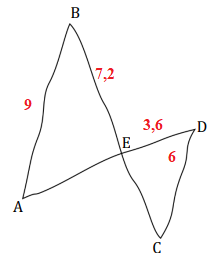Les droites (AB) et (CD) sont parallèles. Les droites (AD) et (BC) sont sécantes en E. On a :  ED = 3,6 cm CD = 6 cm EB = 7,2 cm AB = 9 cm 1) Démontrer que le segment [EC] mesure 4,8 cm. Les deux triangles sont semblables, donc : AB / CD = BE / CE ; 9 / 6 = 7,2 / CE ; CE = 7,2 x 6 / 9 = 4,8 cm.  2) Le triangle ECD est-il rectangle ? ED2 + CE2 = 3,62 +4,82 =36 = 62 = CD2. D'après la réciproque du théorème de Pythagore, le triangle ECD est rectangle en E. 3) Parmi les transformations ci-dessous, quelle est celle qui permet d’obtenir le triangle ABE à partir du triangle ECD ? Recopier la réponse sur la copie. Aucune justification n’est attendue. Symétrie  ; axiale ; Homothétie vrai ; Rotation ; Symétrie centrale ;  Translation.  4) On sait que la longueur BE est 1,5 fois plus grande que la longueur EC. L’affirmation suivante est-elle vraie ? On rappelle que la réponse doit être justifiée. Affirmation : « L’aire du triangle ABE est 1,5 fois plus grande que l’aire du triangle ECD. » Faux. Aire du triangle ABE = BE x AE / 2 = 1,5 x EC x 1,5 x ED = 2,25 x aire du triangle CED. Exercice 3. 20 points. Lors des Jeux paralympiques de 2021, les médias ont proposé un classement des pays en fonction de la répartition des médailles obtenues. Voici le classement obtenu pour les 15 premiers pays : 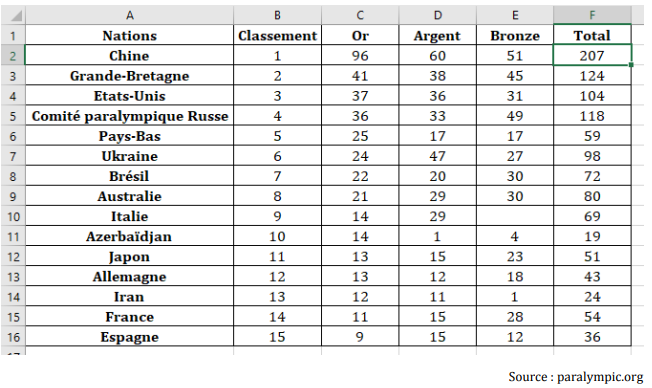1) Combien de médailles d’argent l’Australie a-t-elle obtenues ? 29. 2) Calculer le nombre de médailles de bronze obtenues par l’Italie. 69-14-29=26.  3) Quelle formule a pu être saisie en F2 avant d’être étirée vers le bas ? =Somme(C2:E2)  4) Pour chacune des deux affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées. Affirmation 1 : « 20 % des médailles obtenues par l’équipe de France sont en or. » Vrai. 11 / 54 x100 ~20 %.  Affirmation 2 : « La médiane du nombre de médailles d’argent obtenues par ces 15 pays est 29. » Faux. 1 ; 11 ; 12 ; 15 ; 15 ; 15 ; 17 ; 20 ; 29 ; 29 ; 33 ; 36 ; 38 ; 47 ; 60. 5) Aux Jeux paralympiques de Rio en 2016, la prime pour une médaille d’or française était de 50 000 euros.  Pour ceux de Tokyo en 2021, cette prime était de 65 000 euros. Quel est le pourcentage d’augmentation de cette prime entre 2016 et 2021 ? (65 000 - 50 000) / 50 000 x100 =30 %. ... .... Exercice 4. 25 points. Une boutique en ligne vend des photos et affiche les tarifs suivants : Nombre de photos commandées  de 1 à 100 photos 0,17 € par photo Plus de 100 photos 17 € pour l’ensemble des 100 premières photos et 0,13 € par photo supplémentaire.  1) a. Quel est le prix à payer pour 35 photos ? 35 x 0,17 =5,95 €.  b. Vérifier que le prix à payer pour 150 photos est 23,50 €. 17 + 50 x 0,13 =23,5 €.  c. On dispose d’un budget de 10 €. Combien de photos peut-on commander au maximum ? 10 / 0,17 =58,8 soit 58 photos. On a commencé à construire un programme qui doit permettre de calculer le prix à payer en fonction du nombre de photos commandées : 2) Dans cette question, aucune justification n’est attendue. Par quelles valeurs peut-on compléter les instructions des lignes 3, 4 et 7 pour que le programme permette de calculer le prix à payer en fonction du nombre de photos commandées ? 3) En période des soldes, le site offre une réduction de 30 % sur le prix à payer, pour toute commande supérieure à 20 €.  a. Calculer le prix à payer pour 150 photos en période des soldes. Remise : 23,5 x 0,30 = 7,05 €. Prix à payer : 23,5 -7,05 =16,45 €. Ou bien 23,5 x(1-0,3) =23,5 x0,7 = 16,45 €.  b. Dans cette question, aucune justification n’est attendue. On modifie le programme pour qu’il donne le prix à payer en période des soldes en insérant le bloc ci-contre entre les lignes 8 et 9. Dans la liste suivante, indiquer une proposition qui convient pour compléter la case vide : Exercice 5. 15 points. L’ISS (International Space Station) est une station spatiale internationale placée en orbite autour de la Terre.  1) Dans la journée du 21 juin 2021, l’ISS est passée à la verticale de Canberra (Australie) puis à la verticale de Miami (États-Unis). À l’aide du planisphère ci-dessous, donner les coordonnées géographiques de ces deux villes avec la précision permise par le graphique. On représente la Terre, l’ISS et son orbite (trajectoire de l’ISS) à l’aide du schéma ci-dessous. On considère que :  la Terre est assimilée à une sphère de rayon 6 371 km ;  l’orbite de l’ISS est un cercle de même centre que celui de la Terre ;  l’ISS tourne autour de la Terre à une altitude de 380 km.  2) Montrer que l’ISS parcourt environ 42 400 km pour effectuer un tour complet de la Terre. Circonférence de rayon 6371 +380=6751 km soit 6751 x 2 x3,14 ~42 400 km. 3) On estime que l’ISS tourne autour de la Terre à la vitesse moyenne de 27 600 km/h. a. Montrer qu’il faut environ 1 h 32 min à l’ISS pour effectuer un tour complet de la Terre. distance / vitesse = 42 400 / 27 600 =1,536 h ou 1 h et 0,536 x60 =1 h 32 min. b. Le 19 juin 2020, de 14 h 30 à 21 h 45 (heure de Paris), le spationaute français Thomas Pesquet a effectué une sortie extravéhiculaire en restant attaché à l’ISS. Durant cette sortie, combien de fois Thomas Pesquet a-t-il fait le tour complet de la Terre ? Durée de la sortie : 21 h 45 -14 h30 =7 h 15 min ou 7 x 60 +15 =435 min. 1 h 32 min = 92 min. Nombre de tours : 435 / 92 ~4,7 tours soit 4 tours complets de la terre.

menu