Math�matiques, brevet DNB, Polyn�sie 2022.

Exercice 1. 20 points.
Pour chacune des quatre affirmations suivantes, dire si elle vraie ou fausse en expliquant soigneusement la r�ponse.
1. Adriana doit effectuer le calcul suivant :

Affirmation 1 : Le r�sultat qu’elle obtient sous forme de fraction irr�ductible est − 4 / 35 . Faux.

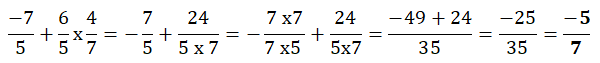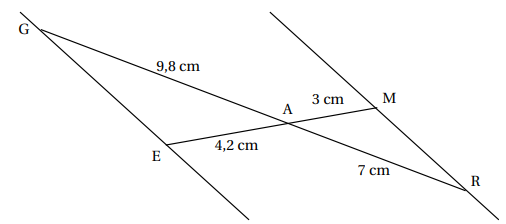
2 . 2. Sur la figure ci-dessous, qui n’est pas � l’�chelle, les points G, A et R sont align�s et les points E, A et M sont align�s.

Affirmation 2 : Les droites (GE) et (MR) sont parall�les. Vrai.
AG / AR = 9,8 / 7 =1,4.
AE / AM = 4,2 / 3 = 1,4.
AG / AR =AE / AM.
D'apr�s la r�ciproque de la propri�t� de Thal�s, les droites (GE) et (MR) sont parall�les.

3. Affirmation 3 : La d�composition en produit de facteurs premiers de 126 est 2�7�9. Faux.
126 = 2 x 3² x9.

4. Dans la recette de sauce de salade de Thomas, les volumes de moutarde, de vinaigre et d’huile sont dans le ratio de 1 : 3 : 7.
Affirmation 4 : Pour obtenir 330 mL de sauce de salade, il faut utiliser 210 mL d’huile. Vrai.
330 / (1+3+7) x 7 = 210 mL d'huile.

Exercice 2 ( 16 points)
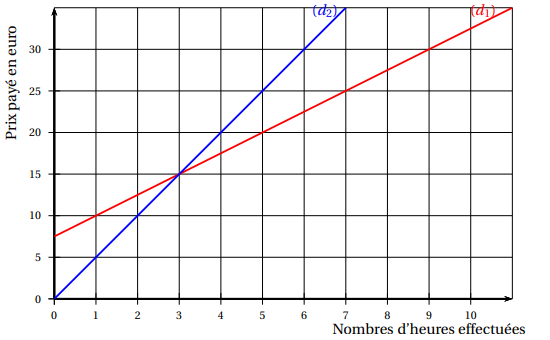
Le graphique ci-dessous repr�sente les deux tarifs pratiqu�s dans une salle de sport, selon le nombre d’heures effectu�es :
• la droite (d₁) est la repr�sentation graphique du tarif � libert� �
• la droite (d₂) est la repr�sentation graphique du tarif � abonn� �

1. Le prix pay� avec le tarif � libert� � est-il proportionnel au nombre d’heures effectu�es dans la salle de sport ? Expliquer la r�ponse.
La droite (d₁) ne passe pas par l'origine. ( fonction affine).
Le prix pay� avec le tarif � libert� � n'est pas proportionnel au nombre d’heures effectu�es dans la salle de sport
2. On appelle :
f la fonction qui, au nombre d’heures effectu�es, associe le prix pay� en euro avec le tarif � libert� �
g la fonction qui, au nombre d’heures effectu�es, associe le prix pay� en euro avec le tarif � abonn� �
R�pondre aux questions suivantes par lecture graphique :
a. Quelle est l’image de 5 par la fonction f ?
f(5) = 20.
b. Quel est l’ant�c�dent de 10 par la fonction g ?
g(2) = 10.
3. � l’aide du graphique, indiquer le tarif parmi les deux propos�s qui est le plus avantageux pour une personne selon le nombre d’heures qu’elle souhaite effectuer dans la salle de sport.
Moins de 3 heures : le tarif abonn� est le plus avantageux.
Plus de 3 heures : le tarif libert� est le plus avantageux.
4. D�terminer le prix pay� avec le tarif � libert� � pour 15 heures effectu�es. Expliquer la d�marche.
f(3) = 15 ; f(7) = 25 ; coefficient directeur de la droite (d1) : (25-15) / (7-3) = 2,5.
Equation de (d₁) : f(x) = 2,5 x +b.
f(3) = 15 = 2,5 *3 +b ; b = 7,5.
f(x) = 2,5 x +7,5.
f(15) = 2,5 *15 +7,5 = 45 €.

Exercice 3. 23 points.
Les deux parties de cet exercice sont ind�pendantes
Une entreprise produit et vend des jus de fruit contenus dans des briques en carton qui ont la forme d’un pav� droit.
PARTIE A : Briques de jus de pomme.
Ces briques sont fabriqu�es pour contenir 350 mL de jus de pomme. Lors d’un contr�le, 24 briques sont pr�lev�es au hasard et analys�es. Le tableau ci-dessous donne le volume de jus de pomme (en mL) contenu dans ces briques :

volume en mL	344	347	348	349	350	351	352	353	354	356	357
effectif	1	2	4	4	2	3	1	2	3	1	1

1. D�terminer la m�diane des volumes de cette s�rie. Interpr�ter ce r�sultat.
24 / 2 = 12.
La m�diane se situe � la 12�me valeur soit 350 mL.
12 bo�tes ont un volume inf�rieur ou �gal � 350 mL
12 bo�tes ont un volume sup�rieur ou �gal � 350 mL.
2. Calculer l’�tendue de cette s�rie
357-344= 13 mL.
3. On pr�l�ve au hasard une brique parmi celles contr�l�es, quelle est la probabilit� qu’elle contienne exactement 350 mL de jus de pomme ?
2 bo�tes sur 24 ; la probabilit� qu’elle contienne exactement 350 mL de jus de pomme est 1/12.
4. Lorsque le volume de jus de pomme contenu dans une brique est compris entre 345 mL et 355 mL, cette brique peut �tre vendue. Quel est le pourcentage de briques que l’entreprise peut vendre parmi les briques contr�l�es ?
21 cas favorables sur 24.
21 / 24 x100 = 87,5 %.
PARTIE B : Briques de jus de raisin.
L’entreprise souhaite commercialiser une nouvelle brique en forme de pav� droit pour le jus de raisin. Sa base est un rectangle de longueur 6,4 cm et de largeur 5 cm.
1. Calculer l’aire de la base de cette brique.
6,4 x 5 =32 cm².
2. Quelle doit �tre la hauteur de cette brique pour que son volume soit de 400 cm³ ?
400 / 32 = 12,5 cm.