Mathématiques, DNB Polynésie 9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1 . 22 points. Cet exercice est constitué de six questions indépendantes. 1. Calculer 5 / 6 + 7/  8 et donner le résultat sous la forme d’une fraction irréductible. On détaillera les calculs. 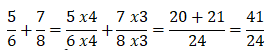 2. a. Donner, sans justifier, la décomposition en facteurs premiers de 198 et de 84. 198 = 2x 32x11. 84 =22 x3 x7. b. En déduire la forme irréductible de la fraction 198 / 84 . 33 / 14.  3. On donne l’expression littérale suivante : E = 5(3x −4)−(2x −7). Développer et réduire E. 15x-20-2x+7=13x-13 = 13(x-1).  4. On désigne par b un nombre positif. Déterminer la valeur de b telle que le périmètre du rectangle ci-contre soit égal à 25. 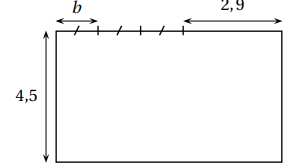Longueur : 3 b +2,9 ; largeur : 4,5. Périmètre = 2(3b +2,9 +4,5) =25. 3b +7,4 = 12,5 ; 3 b = 5,1 ; b =5,1 / 3 =1,7. 5. Calculer le volume de la pyramide à base rectangulaire de hauteur SH = 6 ci-dessous. 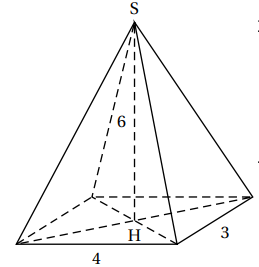Aire de base = 4 x3 = 12 m2. Volume = aire de base x hauteur / 3 = 12 x 6 / 3 =24 m3. 6. Le nombre d’habitants d’une ville a augmenté de 12 % entre 2019 et 2020. Cette ville compte 20 692 habitants en 2020. Quel était le nombre d’habitants de cette ville en 2019 ? 20 692 /(1 +0,12) =18 475.   Exercice 2. 22 points. Un poteau électrique vertical [BC] de 5,2 m de haut est retenu par un câble métallique [AC] comme montré sur le schéma qui n’est pas en vraie grandeur. 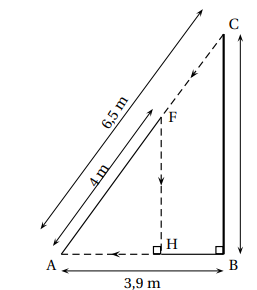 1. Montrer que la longueur du câble [AC] est égale à 6,5 m. Pythagore dans le triangle ABC rectangle en B. AC2 = AB2 + BC2 = 3,92 +5,22 =42,25 ; AC =6,5 m. 2. Calculer la mesure de l’angle ACB au degré près. tan angle ACB = AB / BC = 3,9 / 5,2 =0,75 ; mesure de cet angle ~37°. � Deux araignées se trouvant au sommet du poteau (point C) décident de rejoindre le bas du câble (point A) par deux chemins différents. 3. La première araignée se déplace le long du câble [AC] à une vitesse de 0,2 m/s. Vérifier qu’il lui faut 32,5 secondes pour atteindre le bas du câble. longueur AC / vitesse = 6,5 / 0,2 =32,5 s. 4. La deuxième araignée décide de parcourir le chemin CFHA indiqué en pointillés sur le schéma (qui n’est pas en vraie grandeur) : elle suit le morceau de câble [CF] en marchant, puis descend verticalement le long de [FH] grâce à son fil et enfin marche sur le sol le long de [HA]. Calculer les longueurs FH et HA. Relation de Thalès : FH / BC = AF / AC ; FH = AF x BC / AC = 4 x5,2 / 6,5 =3,2 m. FH / BC =AH / AB ; AH = FH x AB / BC=3,2 x 3,9 / 5,2 =2,4 m. 5. La deuxième araignée marche à une vitesse de 0,2 m/s le long des segments [CF] et [HA] et descend le long du segment [FH] à une vitesse de 0,8 m/s. Laquelle des deux araignées met le moins de temps à arriver en A ? Durée de la marche =(2,5 +2,4) /0,2 =24,5 s. Durée de la descente FH : 3,2 / 0,8 =4 s. Total : 28,5 s. C'est la plus rapide. ... .... Exercice 3. 17 points. On utilise un logiciel de programmation. On rappelle que « s’orienter à 0° » signifie qu’on oriente le stylo vers le haut. On considère les deux scripts suivants. 1. On exécute le script 1. Représenter le chemin parcouru par le stylo.  2. Quel dessin parmi les trois ci-dessous correspond au script 2 ? On expliquera pourquoi les deux autres dessins ne correspondent pas au script 2. Chaque côté de carreau mesure 20 pixels. 3. On souhaite maintenant obtenir le motif représenté sur le dessin suivant. Compléter sans justifier les trois cases du script 3 donné en ANNEXE à rendre avec la copie, permettant d’obtenir le dessin 4.  Compléter sans justifier les trois cases du script suivant permettant d’obtenir le dessin 4. 4. À partir du motif représenté sur le dessin 4, on peut obtenir le pavage ci-dessous : Répondre aux questions suivantes sur votre copie en indiquant le numéro du motif qui convient (on ne demande pas de justifier la réponse) :  a. Quelle est l’image du motif 1 par la translation qui transforme le point B en E ? Motif 5.  b. Quelle est l’image du motif 1 par la symétrie de centre B ? Motif 9. c. Quelle est l’image du motif 16 par la symétrie de centre G ? Motif 12.  d. Quelle est l’image du motif 2 par la symétrie d’axe (CG) ? Motif 5.  EXERCICE 4 20 points.   1. Voici un tableau de valeurs d’une fonction f : x -2 -1 0 1 3 4 5 f(x) 5 3 1 -1 -5 -7 -9 a. Quelle est l’image de 3 par la fonction f ? -5  b. Donner un nombre qui a pour image 5 par la fonction f . -2  c. Donner un antécédent de 1 par la fonction f . 0  2. On considère le programme de calcul suivant : Choisir un nombre ;  Ajouter 1 ; Calculer le carré du résultat.  a. Quel résultat obtient-on en choisissant 1 comme nombre de départ ? 1+1 ; (1+1)2 = 4. Et en choisissant −2 comme nombre de départ ? -2+1 ; (-2+1)2= 1. b. On note x le nombre choisi au départ et on appelle g la fonction qui à x fait correspondre le résultat obtenu avec le programme de calcul. Exprimer g(x) en fonction de x. g(x) = (x+1)2.  3. La fonction h est définie par h(x) = 2x 2 −3.  a. Quelle est l’image de 3 par la fonction h ? h(3) = 2 *32-3 =15.  b. Quelle est l’image de −4 par la fonction h ? h(3) = 2 *(-4)2-3 =32-3 = 29.  c. Donner un antécédent de 5 par la fonction h. En existe-t-il un autre ? 5 = 2x 2 −3 ; 8 = 2x 2 ; 4 = x2 ; x = ±2. 4. On donne les trois représentations graphiques suivantes qui correspondent chacune à une des fonctions f , g et h citées dans les questions précédentes. Associer à chaque courbe la fonction qui lui correspond, en expliquant la réponse. EXERCICE 5 19 points.   Une urne contient 20 boules rouges, 10 boules vertes, 5 boules bleues et 1 boule noire. Un jeu consiste à tirer une boule au hasard dans l’urne. Lorsqu’un joueur tire une boule noire, il gagne 10 points. Lorsqu’il tire une boule bleue, il gagne 5 points. Lorsqu’il tire une boule verte, il gagne 2 points. Lorsqu’il tire une boule rouge, il gagne 1 point. 1. Un joueur tire au hasard une boule dans l’urne.   a. Quelle est la probabilité qu’il gagne 10 points ? Nombre total de boules : 36. Probabilité de tirer une boule noire =1 / 36. b. Quelle est la probabilité qu’il gagne plus de 3 points ? Probabilité de tirer une boule noire ou une boule bleue =6 / 36 =1 / 6.  c. A-t-il plus de chance de gagner 2 points ou de gagner 5 points ? Probabilité de tirer une boule verte =10 / 36 . Probabilité de tirer une boule bleue =5 / 36. Il a plus de chance de gagner 2 points que de gagner 5 points. 2. Le tableau ci-contre récapitule les scores obtenus par 15 joueurs : joueur A B C D E F G H I J K L M N O Total score 2 1 1 5 10 2 2 5 1 2 5 10 1 1 2 50 a. Quelle est la moyenne des scores obtenus par ces joueurs ? 50 / 15 ~3,33. b. Quelle est la médiane des scores ? Score ordonné : 1 ; 1 ; 1 ; 1 ; 1 ; 2 ; 2 ; 2 ; 2 ; 2 ; 5 : 5 ; 5 ; 10 ; 10. c. Déterminer la fréquence du score « 10 points » 2 / 15 ~0,133. 3. Mille joueurs ont participé au jeu. Peut-on estimer le nombre de joueurs ayant obtenu le score de 10 points ? La réponse, affirmative ou négative, devra être argumentée. Probabilité de gagner 10 points fois nombre de joueur : 1 / 36 x 1000 =1000  / 36 ~ 27,8 soit 28 joueurs.

menu