Math�matiques, brevet A��rique du Sud 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
Exercice 1. 24 points.
Pour chacune des six affirmations suivantes, indiquer si elle est vraie ou fausse.
On rappelle que toutes les r�ponses doivent �tre justifi�es.
Affirmation 1 : 72 est un multiple commun des nombres 12 et 18. Vrai.
72 / 12 = 6 ; 72 / 18 =4.
Affirmation 2 : pour tout nombre n, on a l’�galit� suivante : (n −5)2 = n2 −52. Faux.
(n −5)2 = n2 +52-10 n.
On consid�re la fonction f d�finie par f (x) = 2x +5.
Affirmation 3 : l’ant�c�dent de 6 par la fonction f est �gal � 0,5. Vrai.
f(0,5) = 2 *0,5 +5 = 6..
Voici les temp�ratures relev�es en degr� Celsius (not� �C) pendant six jours dans une m�me ville :
5 �C, 7 �C, 11 �C, 8 �C, 5 �C et 6 �C.
Affirmation 4 : la moyenne de ces six temp�ratures est �gale � 6,5 �C. Faux.
(5 +7 +11 + 8 +5 +6) / 6 =7 .
Les points B, D et A sont align�s.
Les points B, E et C sont align�s.
Le triangle ABC est rectangle en B.
BA = 12 cm; BC = 9 cm ; BD = 8 cm et BE = 6 cm.
La figure ci-dessous n’est pas � l’�chelle.

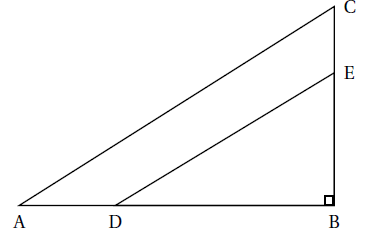
Affirmation 5 : la longueur AC est �gale � 15 cm. Vrai.
AC2 = AB2 +BC2 =122+92=225 ; AC = 15.
Affirmation 6 : les droites (AC) et (DE) sont parall�les. Vrai.
BA / BD = 12 / 8 =1,5 ; BC / BE = 9 / 6 = 1,5.
D'apr�s la r�ciproque du th�or�me de Thal�s, les droites (AC) et (DE) sont parall�les.

Exercice 2. 19 points.
Une m�re et sa fille rentrent chez elles � pied en empruntant le m�me trajet de 10 kilom�tres. La m�re d�cide de s’y rendre en marchant et sa fille en courant.
Le graphique ci-dessous mod�lise les parcours de la m�re et de la fille depuis leur d�part.

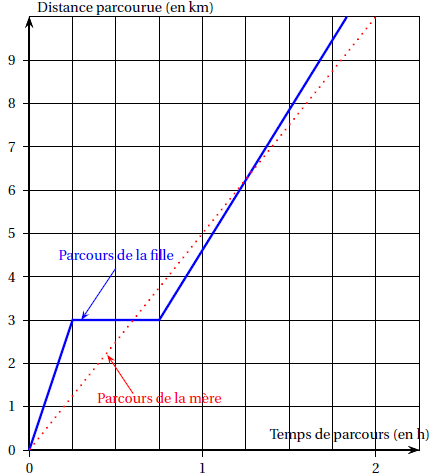
1. a. Indiquer le temps mis par la m�re pour rentrer chez elle, avec la pr�cision que permet la lecture du graphique.
2 heures.
b. D�terminer la vitesse moyenne en km/h de la m�re sur l’ensemble de son parcours.
10 / 2 = 5 km / h.
c. La distance parcourue par la m�re est-elle proportionnelle au temps ?
Oui : le graphe en pointill�s rouges est une droite passant par l'origine.
2. La fille est partie � 16 h et est arriv�e chez elle � 17 h 50. Elle a fait une pause durant sa course.
a. Indiquer la dur�e de la pause de la fille, avec la pr�cision que permet la lecture graphique.
0,5 heure.
b. Quand a-t-elle couru le plus vite : avant ou apr�s sa pause ?
Avant la pause, vitesse de la fille : 3 / 0,25 = 12 km / h.
Apr�s la pause, vitesse de la fille : 7 / 1,1 ~ 6,4 km / h.
3. Combien de fois la m�re et la fille se sont retrouv�es au m�me endroit et au m�me moment, au cours de leur trajet ?
Les courbes se coupent en deux endroits. La m�re et la fille se sont retrouv�es 2 fois au m�me endroit et au m�me moment.
4. Dans cette question, on note f la fonction qui, au temps de parcours x (exprim� en heure) de la m�re depuis le d�part, associe la distance parcourue (exprim�e en kilom�tre) par la m�re depuis le d�part.
Parmi les propositions suivantes, recopier sans justification l’expression de f (x) :
f (x) =x / 5 ; f(x) = 5x ; f(x) = x+5.

Exercice 3. 23 points.
Un club de handball souhaite commander des maillots avec le nom du club inscrit dessus. � l’issue de sa commande, le club veut recevoir exactement 350 maillots. Apr�s quelques recherches, deux sites internet ont �t� s�lectionn�s :
• sur le site A : les maillots sont vendus � 12 € l’unit�;
• sur le site B : les maillots sont vendus � 13 € l’unit�, avec la promotion :
� 10 maillots offerts pour 100 achet�s �.
1. D�terminer le montant, exprim� en euro, de la commande du club envisag�e sur le site A.
350 x 12 = 4200 €.
2. Un tableur ci-dessous pr�sente des exemples de d�penses en fonction du nombre de maillots pay�s sur le site B. Voici une copie d’�cran de ce tableur.

a. � la lecture de ce tableur, le tr�sorier du club affirme que le montant de la commande sera compris entre 3 900 € et 4 550 €. Son affirmation est-elle vraie ?
30 maillots sont offerts ; 320 sont pay�s : 320 x13 =4160 €. Affirmation vraie.
b. Sachant que les lignes 1 et 2 du tableur ont �t� compl�t�es auparavant, quelle formule a t-on pu saisir ensuite dans la cellule B3 avant de l’�tirer jusqu’� la cellule I3, pour remplir la ligne 3 du tableur ?
=B1+B2
c. Le co�t total exprim� en euro est-il proportionnel au nombre de maillots re�us ?
Non : 650 / 50 = 13 ; 1300 / 110 ~11,82 ; 1950 / 160 ~12,19.
3. Sur quel site le club doit-il passer sa commande pour recevoir exactement 350 maillots, tout en payant le moins cher ?
A : 4200 € ; B : 4160 €, donc B.
4. Le club souhaite que ces 350 maillots soient r�partis entre des maillots noirs et des maillots rouges dans le ratio 5 : 2.
Combien faut-il commander de maillots noirs et de maillots rouges ?
350 / (5+2) = 50 ; 50 x5 = 250 noirs et 50 x2 = 100 rouges.
5. Le club a aussi command� des gourdes. Les cartons re�us sont indiscernables tant par leurs dimensions que par leur forme.
Il y a 4 cartons de gourdes blanches et 3 cartons de gourdes bleues.
On ouvre un carton au hasard. Quelle est la probabilit� qu’il contienne des gourdes bleues ?
3 /(4+3) =3 / 7 ~0,43.

...
....

 Exercice 4. 14 points.
Dans tout cet exercice, aucune justification n’est demand�e
On donne le programme suivant :

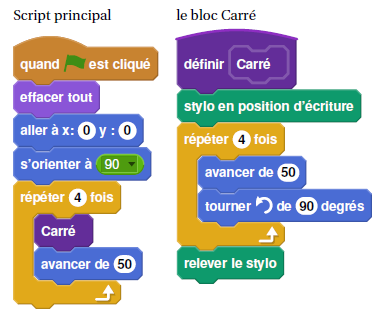
On rappelle que l’instruction s’orienter � 90 signifie que l’on s’oriente vers la droite.
1. On lance le programme.
Construire la figure obtenue en prenant 1 cm pour 25 unit�s de longueur.

On modifie le Script principal et on obtient deux scripts ci-dessous :

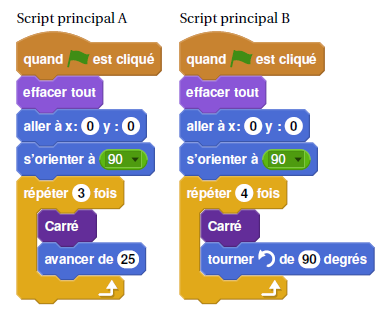
2. Parmi les trois figures ci-dessous, associer sur votre copie chacun des deux scripts principaux A et B � la figure qu’il permet de r�aliser :


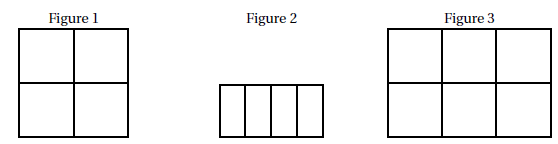
Script A : figure 2 ; script B : figure 1.
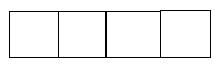
On souhaite r�aliser la figure suivante :

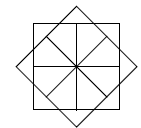
Le point de d�part se situe au centre de la figure.
3. Compl�ter le nouveau script principal ci-dessous en recopiant sur la copie uniquement les lignes 5 et 7. Pour m�moire, l’�nonc� rappelle ci-dessous � droite le descriptif du bloc Carr�.


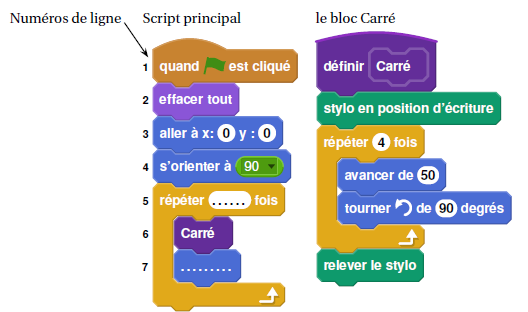
Ligne 5 ; r�p�ter 8 fois ; ligne 7 : tourner de 45�.

Exercice 5. 20 points
Une usine de fabrication de bougies re�oit des cubes de cire d’abeille d’ar�te 6 cm.
Ils sont dispos�s dans des cartons remplis (sans espace vide).
Informations sur les cartons :
Forme : pav� droit
Dimensions :
— largeur : 60 cm
— hauteur : 36 cm
— profondeur : 36 cm
(On ne tient pas compte de l’�paisseur des cartons)
Information sur la cire d’abeille :
Masse volumique : 0,95 g/cm3.
1. a. Montrer que chaque carton contient 360 cubes de cire d’abeille.
Volume du cube de cire : 63 =216 cm3.
Volume du carton : 60 x 36 x 36 =77 760 cm3.
Nombre de cube : 77 760 / 216 =360.
b. Quelle est la masse de cire d’abeille contenue dans un carton rempli de cubes ? On donnera la r�ponse en kg, arrondie � l’unit� pr�s, en ne tenant pas compte de la masse du carton.
77 760 x0,95 / 1000 ~74 kg.
2. � l’usine, on d�coupe les cubes de cire d’abeille afin d’obtenir des cylindres de hauteur 6 cm et de diam�tre 6 cm avec lesquels on fera des bougies en installant une m�che.
On ne tiendra pas compte de la masse, du volume et du prix de la m�che dans la suite de l’exercice.
a. Montrer que le volume-d’une bougie est d’environ 170 cm3.
On rappelle que le volume d’un cylindre de rayon r et de hauteur h est donn� par la formule V =pr2h.
3,14 x32 x6 ░170 cm3.
b. En d�coupant les cubes de cire d’abeille d’ar�te 6 cm pour former des bougies cylindriques, la cire perdue est r�utilis�e pour former � nouveau d’autres cubes de cire d’abeille d’ar�te 6 cm.
Combien de cubes au d�part doit-on d�couper pour pouvoir reconstituer un cube de cire d’abeille d’ar�te 6 cm, avec la cire perdue ?
Volume de cire perdue pour un cube : 216-170=46 cm3.
Nombre de cube : 216 / 46 ~4,7 soit 5 cubes de d�part.
3. Un commer�ant vend les bougies de cette usine au prix de 9,60 € l’unit�. Il les vend 20% plus ch�res qu’il ne les ach�te � l’usine.
Combien paie-t-il � l’usine pour l’achat d’une bougie ?
Prix d'achat * 1,20 = prix de vente.
Prix d'achat = 9,60 / 1,20 =8,0 €.

  
menu